6.1 数据结构---树（遍历）
一、树的定义
1.定义
树是n(n>=0)个节点的有限集，且这些节点满足如下关系：
（1）有且仅有一个节点没有父节点，该节点称为树的根；
（2）除根外，其余的每个节点都有且仅有一个父节点；
（3）树中的每一个节点都构成一个以它为根的树。
二叉树在满足树的条件时，满足如下条件：每个节点最多有两个孩子（子树），这两个子树有左右之分，次序不可颠倒。
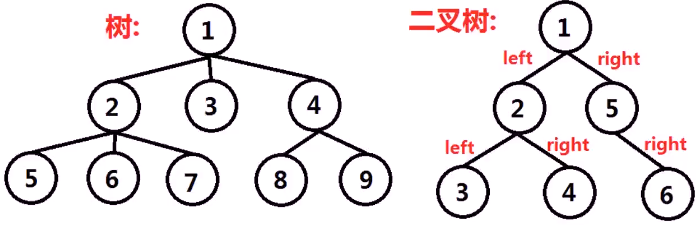
2.树的遍历
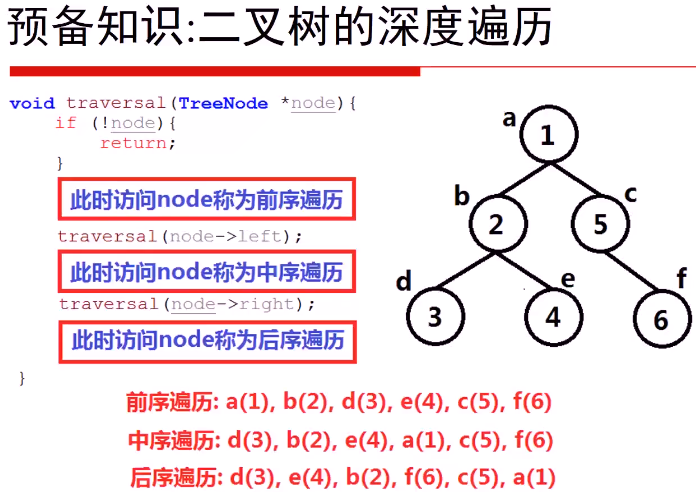
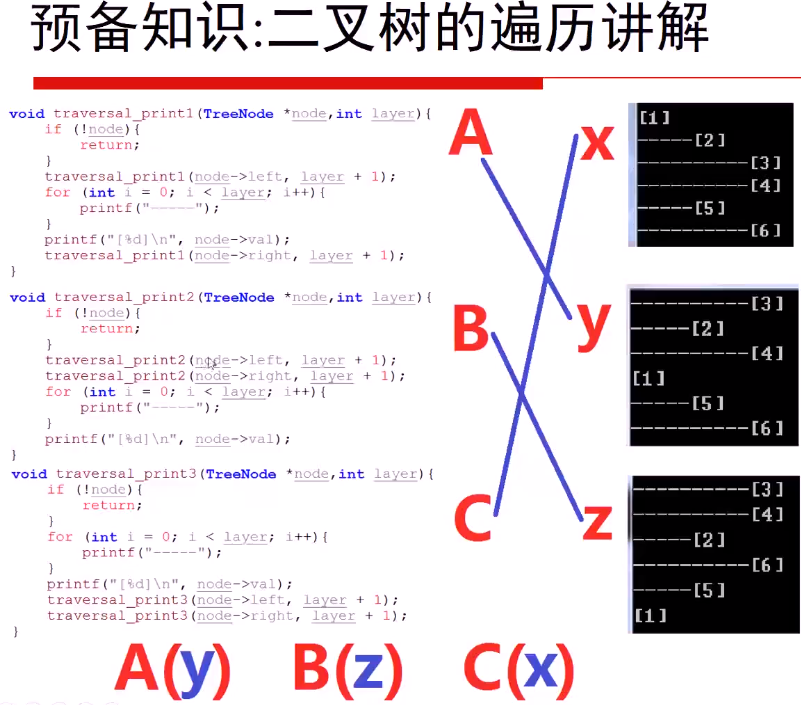
二、先序遍历
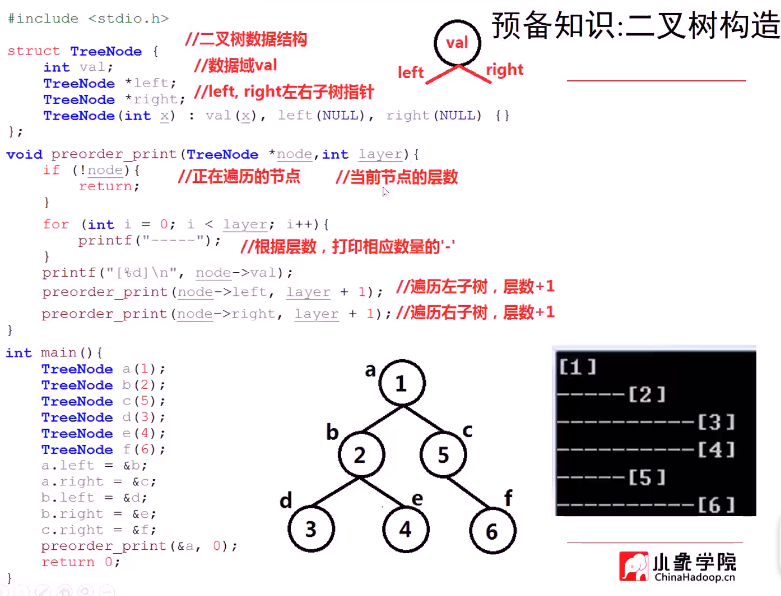
1.先序遍历
递归
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def preorderTraversal(self,root):
'''
递归,时间复杂度O(n),空间复杂度平均O(logn),最坏情况下O(n)
:param root:
:return:
'''
if root:
print(root.val)
else:
return
self.preorderTraversal(root.left)
self.preorderTraversal(root.right)
非递归：时间复杂度O(n),空间复杂度O(n)
思路:
1)申请一个新的栈,把头结点压入栈中
2)从栈中弹出栈顶节点,记为node,然后打印node节点的值,再将节点node的由孩子先压入stack中,最后将node的左孩子压入stack中
3)不断重复步骤2,直到栈为空,过程结束
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def preorderTraversal1(self,root):
'''
:param root:
:return:
'''
if root == None:
return
res = []
stack = [root]
while stack:
node = stack.pop()
print(node.val)
res.append(node.val)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return res
2.左叶子之和
leetcode 404
3.判断一棵树是不是平衡树
4.复制二叉树
5.求二叉树的所有叶子节点，并且判断两棵二叉树的叶子节点是否相等
思路1：用先序遍历按左到右顺序遍历所有叶子节点，并返回，然后判断两棵树的叶子序列是否相等。
时间复杂度O(T1+T2) 空间复杂度O(T1+T2)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def leafSimilar(self, root1: TreeNode, root2: TreeNode) -> bool:
values1,values2=[],[]
self.printleaf(root1,values1)
self.printleaf(root2,values2)
if values1 == values2:
return True
else:
return False
def printleaf(self,root,values):
if root == None:
return
if root.left == None and root.right == None:
values.append(root.val)
self.printleaf(root.left,values)
self.printleaf(root.right,values)
思路2：dfs
class Solution:
def leafSimilar(self, root1, root2):
def dfs(node):
if node:
if not node.left and not node.right:
yield node.val
yield from dfs(node.left)
yield from dfs(node.right)
return list(dfs(root1)) == list(dfs(root2))
三、中序遍历
1.中序遍历
递归：时间复杂度O(n),空间复杂度平均O(logn),最坏情况下O(n)
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def inorderTraversal(self,root):
'''
:param root:
:return:
'''
if root == None:
return
self.inorderTraversal(root.left)
print(root.val)
self.inorderTraversal(root.right)
非递归：时间复杂度O(n),空间复杂度O(n)
思路:
1)申请一个新的栈,初始时,令变量node=head
2)先把node节点压入栈中,对以node节点为头的整棵子树来说,依次把左边界压入栈中,即不停的令node=node.left,然后重复步骤2
3)不断重复步骤2,直到发现node为空,此时,从栈中弹出一个节点,记为node,打印node的值,并且让node=node.right,然后继续重复步骤2
4)当stack为空且cur为空时,整个过程停止.
class Solution:
def inorderTraversal1(self,root):
'''
:param root:
:return:
'''
if root == None:
return
res = []
stack = []
node = root
while stack or node:
if node:
stack.append(node)
node = node.left
else:
node = stack.pop()
res.append(node.val)
node = node.right
return res
2.判断一棵树是不是二叉搜索树
3.在二叉排序树中找出第一个大于中间值的借贷
4.二叉树转换为双向链表
四、后序遍历
1.后序遍历
递归：时间复杂度O(n),空间复杂度平均O(logn),最坏情况下O(n)
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def posorderTraversal(self,root):
'''
:param root:
:return:
'''
if root == None:
return
self.posorderTraversal(root.left)
self.posorderTraversal(root.right)
print(root.val)
非递归
a.两个栈：时间复杂度O(n),空间复杂度O(n)
思路：用两个栈实现后序遍历
1)申请一个栈,记为s1,然后将头结点head压入栈Ss1中;
2)从s1中弹出的节点记为cur,然后依次将cur的左孩子和右孩子压入s1中;
3)从整个过程中,每一个从s1中弹出的节点都放进s2中;
4)不断重复步骤2和步骤3,直到s1为空,过程停止;
5)从s2中依次弹出节点并打印,打印的顺序就是后序遍历的顺序.
class Solution:
def posorderTraversal1(self,root):
'''
:param root:
:return:
'''
if not root:
return []
s1,s2 = [root],[]
while s1:
cur = s1.pop()
s2.append(cur.val)
if cur.left:
s1.append(cur.left)
if cur.right:
s1.append(cur.right)
return s2[::-1]
b.一个栈
思路：用一个栈实现后序遍历
申请一个栈,将头结点压入栈中,同时设置变量h和c,h代表最近一次弹出并打印的节点,c代表stack的栈顶节点,初始时h为头结点,c为null
def posorderTraversal2(self,root):
'''
:param root:
:return:
'''
if not root:
return []
res = []
cur = [root]
while cur:
node = cur[-1]
if node.left and node.left != root and node.right != root:
cur.append(node.left)
elif node.right and node.right != root:
cur.append(node.right)
else:
res.append(cur.pop().val)
root = node
return res
2.二叉树的最小深度
leetcode 111
3.判断一个数组是否是二元查找树后序遍历的序列
4.对二叉树进行镜像反转
5.求二叉树的最大子树和
五、层次遍历
1.层次遍历
递归
思路：每次遍历到新层，层数+1,
class Solution:
def levelOrder(self,root,level,result):
'''
递归,按层输出
:param root:
:param level:
:param result:
:return:
'''
if root == None:
return
if level == len(result): # 如果遍历到了新层,就新建一个[]用来存放新层的值
result.append([])
result[level].append(root.val)
if root.left:
self.levelOrder(root.left,level+1,result)
if root.right:
self.levelOrder(root.right,level+1,result)
def levelOrder1(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
level,result = 0,[]
self.levelOrder(root,level,result)
return result
非递归
思路：用一个队列记录
def levelOrder2(self,root):
'''
思路:队列
用队列存储节点,每次左边出一个节点,如果该节点有左右节点,就将左右节点入队列,直到队列空为止
:param root:
:return:
'''
from collections import deque
if root == None:
return
queue = deque()
queue.append(root)
res = []
while queue:
node = queue.popleft()
res.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
2.二叉树的锯齿形层次遍历 leetcode103
3.二叉树自底向上层次遍历
4.判断一棵树是不是二叉完全树
5.找树左下角的值 leetcode153
思想：层次遍历找最后一层的第一个节点的值
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def findBottomLeftValue(self, root: TreeNode) -> int:
#层次遍历，找最后一层的第一个数
self.res = []
def levelOrder(root,level):
if not root:
return
if len(self.res) == level:#如果层数和res里面的长度相等，说明该层已经遍历完，或者是第一次遍历，就新建一个[]，用来放下一层的数据
self.res.append([])
self.res[-1].append(root.val)
if root.left:
levelOrder(root.left,level+1)
if root.right:
levelOrder(root.right,level+1)
if not root:
return
if not root.left and not root.right:
return root.val
levelOrder(root,0)
return self.res[-1][0]
六、给定二叉树前、中序遍历，构造二叉树
分析：
前序遍历序列第一个是根节点x
从中序遍历序列中找到根节点x
中序遍历中x的左边序列对应等长的前序遍历序列【左子树】
中序遍历中的x的右边序列对应等长的前序遍历序列【右子树】
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def buildTree(preorder,inorder):
if preorder == []:
return None
val = preorder[0]
idx = inorder.index(val)
l_inorder = inorder[0:idx]
r_inorder = inorder[idx+1:]
l_preorder = preorder[1:1+len(l_inorder)]
r_preorder = preorder[1+len(l_inorder):]
root = TreeNode(val)
root.left = buildTree(l_preorder,l_inorder)
root.right = buildTree(r_preorder,r_inorder)
return root
七、给定二叉树中、后序遍历，构造二叉树
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def buildTree(inorder,postorder):
if postorder == []:
return None
val = postorder[-1]
idx = inorder.index(val)
l_inorder = inorder[0:idx]
r_inorder = inorder[idx+1:]
l_postorder = postorder[:len(l_inorder)]
r_postorder = postorder[len(l_inorder):-1]
root = TreeNode(val)
root.left = buildTree(l_inorder,l_postorder)
root.right = buildTree(r_inorder,r_postorder)
return root
