深度学习优化方法

SGD > SGDM > NAG > AdaGrad > AdaDelta > RMSprop > Adam > AdaMax > Ndam > AMSGrad

优化算法的框架：

• 待优化参数：$w$，目标函数：$f(w)$，初始学习率$\alpha$
• 每个epoch $t$：
1. 计算目标函数关于当前参数的梯度：$g_t = \Delta f(w_t)$；
2. 根据历史梯度计算一阶动量和二阶动量$m_t=\phi (g_1,g_2,...,g_t)$，$V_t = \psi (g_1,g_2,...,g_t)$；
3. 计算当前时刻的下降梯度$\eta _t = \frac{\alpha m_t}{V_t}$
4. 更新参数$w_{t+1}=w_t - \eta _t$

TensorFlow提供11个优化器：

• Tf.train.AdadeltaOptimizer
• Tf.train.AdagradDAOptimizer
• Tf.train.AdagradOptimizer
• Tf.train.AdamOptimizer
• Tf.train.FtrlOptimizer
• Tf.train.GradientDescentOptimizer
• Tf.train.MomentumOptimizer
• Tf.train.ProximalAdagradOptimizer
• Tf.train.ProximalGradientDescentOptimizer
• Tf.train.RMSPropOptimizer
• Tf.train.SyncReplicasOptimizer

一、梯度下降法的变形

1.SGD

$g_t$	$g_t = \Delta f(w_t)$
$m_t$，$V_t$	SGD没有动量的概念，$m_t=g_t$，$V_t=I^2$
$\eta _t$	$\eta _t = \alpha g_t$
$w_{t+1}$	$w_t-\eta_t=w_t-\alpha g_t$

TensorFlow用法

缺点：下降速度快，收敛速度慢

2.BGD

查看详情

3.mini-batch GD

查看详情

 

梯度下降法的挑战：

• 学习率如何选择？对所有参数更新使用相同的学习率，对稀疏数据和频率差异大的数据不友好
• 如何使函数逃出鞍点？即那些在一个维度上是递增的，而在另一个维度上是递减的。这些鞍点通常被具有相同误差的点包围，因为在任意维度上的梯度都近似为0，所以SGD很难从这些鞍点中逃开。

 

二、梯度下降优化算法

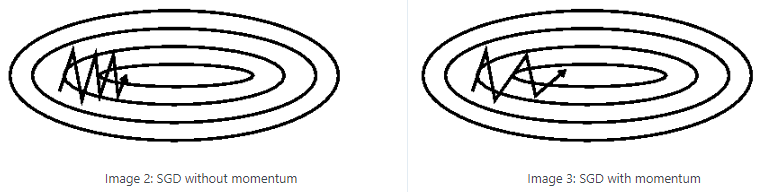
2.1 SGD with Momentum（SGD-M）

　　为了抑制SGD的震荡，SGDM认为梯度下降过程可以加入惯性。下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些。在SGD基础上引入了一阶动量，一阶动量是各个时刻梯度方向的指数移动平均值。

$g_t$	$g_t = \Delta f(w_t)$
$m_t$，$V_t$	$m_t=\beta _1  m_{t-1} + (1- \beta _1)g_t$，$\beta _1$的经验值为0.9
$\eta_t$	$\eta_t = \alpha m_t$
$w_{t+1}$	$w_{t+1}=w_t-\eta _t = w_t-\alpha m_t = w_t - \alpha (\beta _1 m_{t-1} + (1-\beta _1)g_t)$

TensorFlow用法

 

2.2 SGD with Nesterov Acceleration（NAG，Nesterov Accelerated Gradient）

　　NAG全称Nesterov Accelerated Gradient，是在SGD、SGD-M的基础上的进一步改进，改进点在于步骤1。我们知道在时刻t的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算，那与其看当前梯度方向，不如先看看如果跟着累积动量走了一步，那个时候再怎么走。因此，NAG在步骤1，不计算当前位置的梯度方向，而是计算如果按照累积动量走了一步，那个时候的下降方向，然后用下一个点的梯度方向，与历史累积动量相结合，计算步骤2中当前时刻的累积动量。

$g_t$	$g_t=\Delta f(w_t-\alpha m_{t-1} / \sqrt{V_{t-1}})$
$m_t$，$V_t$	$m_t=\beta _1 m_{t-1} + (1- \beta _1)g_t$
$\eta_t$	$\eta_t = \alpha m_t$
$w_{t+1}$	$w_{t+1}=w_t-\eta _t = w_t -  \alpha m_t = w_t - \alpha (\beta _1 m_{t-1} + (1-\beta _1)g_t)$

 

然后用下一个点的梯度方向，与历史累积动量相结合，计算步骤2中当前时刻的累积动量。

 

---

SGD及其变种以同样的学习率更新每个参数，但深度神经网络往往包含大量的参数，这些参数并不是总会用得到。对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。

2.3 AdaGrad

$g_{t,i}$	$g_{t,i} = \Delta f(w_{t,i})$
$m_{t,i}$，$V_{t,i}$	$m_t=g_t$，$V_{t,i} = V_{t-1,i}+g_{t,i}^2=\sum_{\tau=1}^{t}g_{\tau,i}^2$
$\eta _{t,i}$	$\eta _{t,i} = \alpha m_{t,i} /{ \sqrt {V_{t,i}+ \epsilon}}$，      一般为了避免分母为0，会在分母上加一个小的平滑项，$\epsilon$通常取1e-8
$w_{t+1,i}$	$w_{t+1,i} = w_{t,i} - \eta _{t,i} = w_t - \alpha m_{t,i} / {\sqrt {V_{t,i}+ \epsilon}}=w_{t,i} - \frac{\alpha m_{t,i}}{\sqrt{\sum_{\tau=1}^{t}g_{\tau,i}^2+\epsilon}}$

　　AdaGrad让学习率适应参数（学习率实际上由$\alpha$变成了$\alpha / \sqrt {V_t+\epsilon}$），对于出现次数较少的特征，对其使用更大的学习率；对于出现次数较多的特征，对其采用较小的学习率。适合处理稀疏数据，为什么适合？？？

缺点：

• 由公式可以看出，仍依赖于人工设置一个全局学习率$\alpha$，$\alpha$设置过大的话，会使regularizer过于敏感，对梯度的调节太大,通常采用0.01
• 由于没增加一个正项，在整个训练过程中，累加的和会持续增长。这会导致学习率变小以至于最终变得无限小，在学习率无限小时，Adagrad算法将无法取得额外的信息

2.4 AdaDelta

　　Adadelta是Adagrad的一种扩展算法，以处理Adagrad学习速率单调递减的问题。不是计算所有的梯度平方，Adadelta将计算计算历史梯度的窗口大小限制为一个固定值w。Vt　　

先前得到的adagrad参数更新向量为$\eta _{t} = \alpha m_{t} /{ \sqrt {V_{t}+ \epsilon}}$

将对角矩阵$V_{t}$替换成历史梯度的均值$E[g^2]_t$，$\eta _{t} = \alpha m_{t} /{ \sqrt {E[g^2]_t+ \epsilon}}$

将分母的均方根误差记作$RMS[g]_t=E[g^2]_t+ \epsilon$，所以，$\eta _{t} = \alpha m_{t} /{RMS[g]_t}$，

作者引入一个指数衰减均值，这次不是梯度平方，而是参数的平方的更新：为什么要引入，不引入会怎么样？？？

$E[\eta ^2]_t=pE[\eta ^2]_{t-1}+(1-p)\eta _t ^2$

因此，参数更新的均方根误差为$RMS[\eta]_t=\sqrt {E[\eta ^2]_t + \epsilon}$，

由于$RMS[\eta]_t$是未知的，我们利用参数的均方根误差来近似更新，利用$RMS[\eta]_{t-1}$替换先前更新规则中的学习率$\alpha$，最终得到adadelta的更新规则为:

$g_t$	$g_t = \Delta f(w_t)$
$m_t$，$V_t$	$m_t = g_t$，$V_t=E[g^2]_t$
$\eta_t$	$\eta _t = \frac{RMS[\eta]_{t-1}}{RMS[g]_{t-1}}g_t$
$w_{t+1}$	$w_{t+1} = w_t - \eta _t = w_t - \frac{RMS[\eta]_{t-1}}{RMS[g]_{t-1}}g_t$

使用Adadelta算法，我们甚至都无需设置默认的学习率，因为更新规则中已经移除了学习率。

 

特点：

• 训练初中期，加速效果不错，很快
• 训练后期，反复在局部最小值附近抖动

2.5 RMSProp（root mean square prop）

• 作者：Geoff Hinton
• 文章：http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf

　　RMSProp是与Adadelta在相同时间里提出来的，都起源于对adagrad的极速递减的学习率问题的求解，与adadelta不同的是，RMSProp的学习率$\alpha$仍需要手动设置。

$g_t$	$g_t = \Delta f(w_t)$
$m_t$，$V_t$	$m_t = g_t$，$V_t=E[g^2]_t=p*E[g^2]_{t-1}+(1-p)*g_t^2$
$\eta _t$	$\eta _t = \frac{\alpha}{RMS[g]_{t-1}}g_t$
$w_{t+1}$	$w_{t+1} = w_t - \eta _t = w_t - \frac{\alpha}{RMS[g]_{t-1}}g_t$，     $alpha$一般取0.001

特点：

• 其实RMSprop依然依赖于全局学习率
• RMSprop算是Adagrad的一种发展，和Adadelta的变体，效果趋于二者之间
• 适合处理非平稳目标 - 对于RNN效果很好

2.6 Adam（Adaptive moment estimation）

　　我们看到，SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。（有没有用到alpha？）

$g_t$	$g_t = \Delta f(w_t)$
$m_t$，$V_t$	$m_t=\beta _1 m_{t-1} + (1-\beta _1)g_t$，$V_t=\beta _2 V_{t-1}+(1-\beta _2)g_t^2$
$\eta _t$	$\eta _t = \frac{\alpha m_t}{V_t}$
$w_{t+1}$	$w_{t+1} = w_t - \eta _t$

 $m_t$和$V_t$分别是对梯度的一阶矩（均值）和二阶矩（非确定的方差）的估计，当 $m_t$和$V_t$初始化为0向量时，Adam的作者发现它们都偏向于0，尤其是在初始化的步骤和当衰减率很小的时候（例如$beta _1$和$beta _2$都趋向于1）

通过计算偏差校正的一阶矩和二阶矩估计来抵消偏差

$$\hat{m_t} = \frac{m_t}{1-\beta _1^t}$$

$$\hat{V_t} = \frac{V_t}{1-\beta _2^t}$$

由此生成了Adam的更新规则$w_{t+1} = w_t - \eta _t=w_t - \frac{alpha \hat{m_t}}{\sqrt{\hat{v_t}+\epsilon}}$

通常，$beta _1$取0.9，$beta _2$取0.999，$\epsilon$为$10^{-8}$

2.7 Ndam

Nesterov + Adam = Nadam

$g_t$	$g_t=\Delta f(w_t-\alpha m_{t-1} / \sqrt {V_t})$
$m_t$，$V_t$
$\eta_t$
$w_{t+1}$

 

 

 

参考文献：

【1】An overview of gradient descent optimization algorithms

【2】一个框架看懂优化算法之异同 SGD/AdaGrad/Adam

【3】深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）

【4】keras优化器

【5】梯度下降优化算法综述(英文版的翻译版本）