Graph Embedding总结
图嵌入应用场景：可用于推荐，节点分类，链接预测（link prediction），可视化等场景
一、考虑网络结构
1.DeepWalk （KDD 2014）
（1）简介
- DeepWalk = Random Walk + Skip-gram
- 论文链接
- 作者：Bryan Perozzi, Rami Al-Rfou, Steven Skiena
- 主要思想：
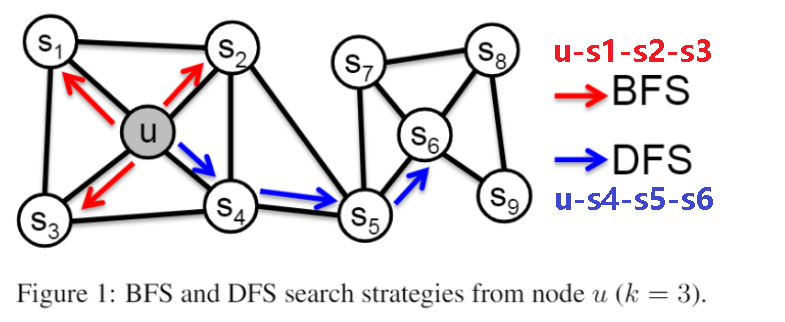
- 假设邻域相似，使用DFS构造邻域
- step1：DeepWalk思想类似word2vec，word2vec是通过语料库中的句子序列来描述词与词的共现关系。关键问题是如何描述节点与节点的共现关系。DeepWalk是给定当前访问起始节点，从其邻居中随机采样节点作为下一个访问节点，重复此过程，直到访问序列长度满足预设条件，产生大量词序列（句子）；
- step2：然后将这些词序列作为训练样本输入word2vec，用Skip-gram + Hierarchical softmax进行训练，得到词的embedding。
- 适用场景：只适用于无权边，仅利用二阶相似度
（2）举例
- 数据集：wiki数据集（2405个网页，17981条网页间的关系）
- 输入样本：node1 node2 <edge_weight>
- 输出：每个node的embedding
- 实现代码
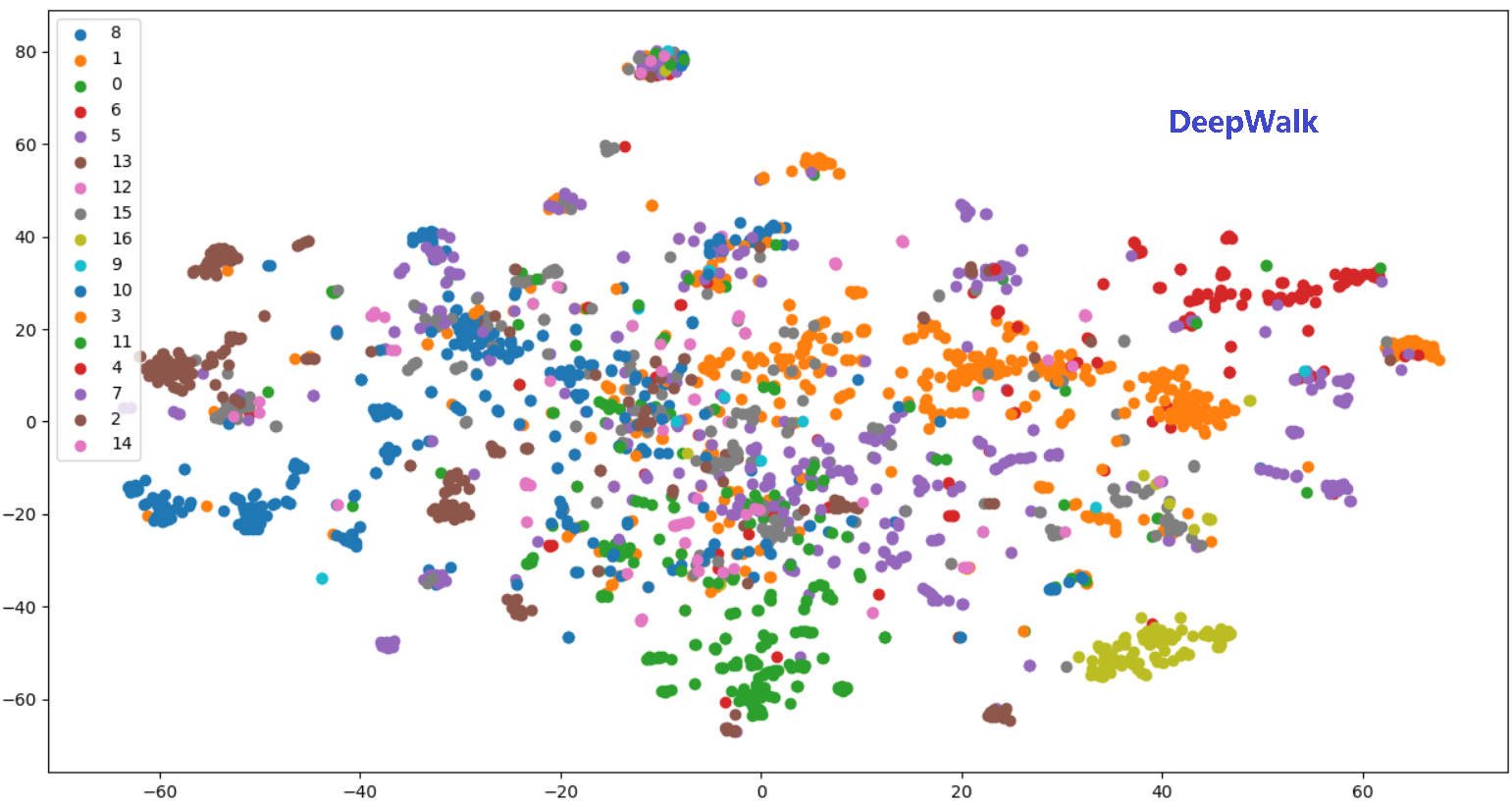
- 效果：比较临近的节点在 Embedding 空间更为接近，且结构更为相似的节点，距离也更近。这就是网络节点的同质性（homophily）和结构性（structural equivalence）
2.LINE（Large-scale Information Network Embedding）（WWW 2015）
（1）简介
- 论文链接
- 作者：Jian Tang, Meng Qu , Mingzhe Wang, Ming Zhang, Jun Yan, Qiaozhu Mei
- 主要思想：
- 假设邻域相似，利用DFS（一阶）、BFS（二阶）构造邻域
- 一些定义：
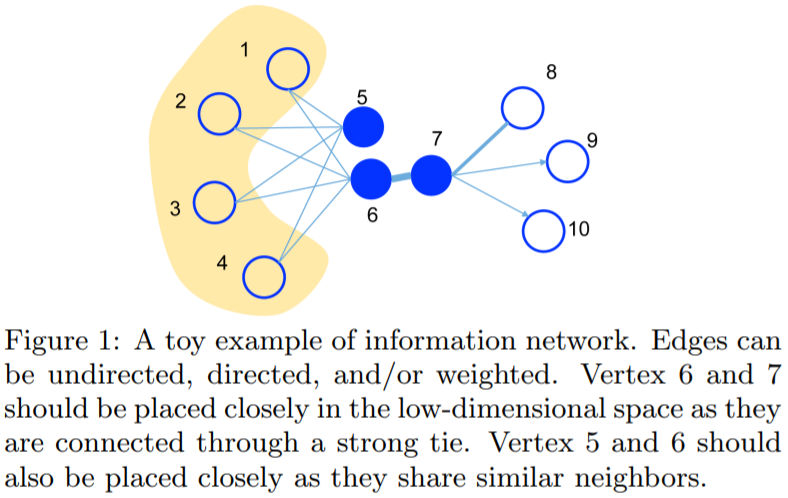
- First-order proximity（1 阶相似度，同质性相似，仅适用于无向图）：用于描述图中成对顶点之间的局部相似度，形式化描述为若节点之间存在直连边，则边的权重即为两个顶点的相似度，若不存在直连边，则 1 阶相似度为0。 如下图，节点 6 和 7 之间存在直连边，且边权较大，则认为两者相似且 1 阶相似度较高，而 5 和 6 之间不存在直连边，则两者间 1 阶相似度为 0。
- Second-order proximity（2 阶相似度，结构性相似，适用于无向图|有向图）：仅有1阶相似度显然不够，如下图，虽然节点 5 和 6 之间不存在直连边，但是他们有很多相同的相邻节点 （1,2,3,4），这其实也可以表明5和6是相似的，而 2 阶相似度就是用来描述这种关系的。 形式化定义为，令表示顶点 u 与所有其他顶点间的1阶相似度，则 u 与 v 的2阶相似度可以通过 $p_u$ 和 $p_v$ 的相似度表示。若u与v之间不存在相同的邻居顶点，则2阶相似度为0。
- 适用场景：
- 一阶相似度仅适用于无向图,而不适用于有向图；
- 二阶相似度
（2）举例
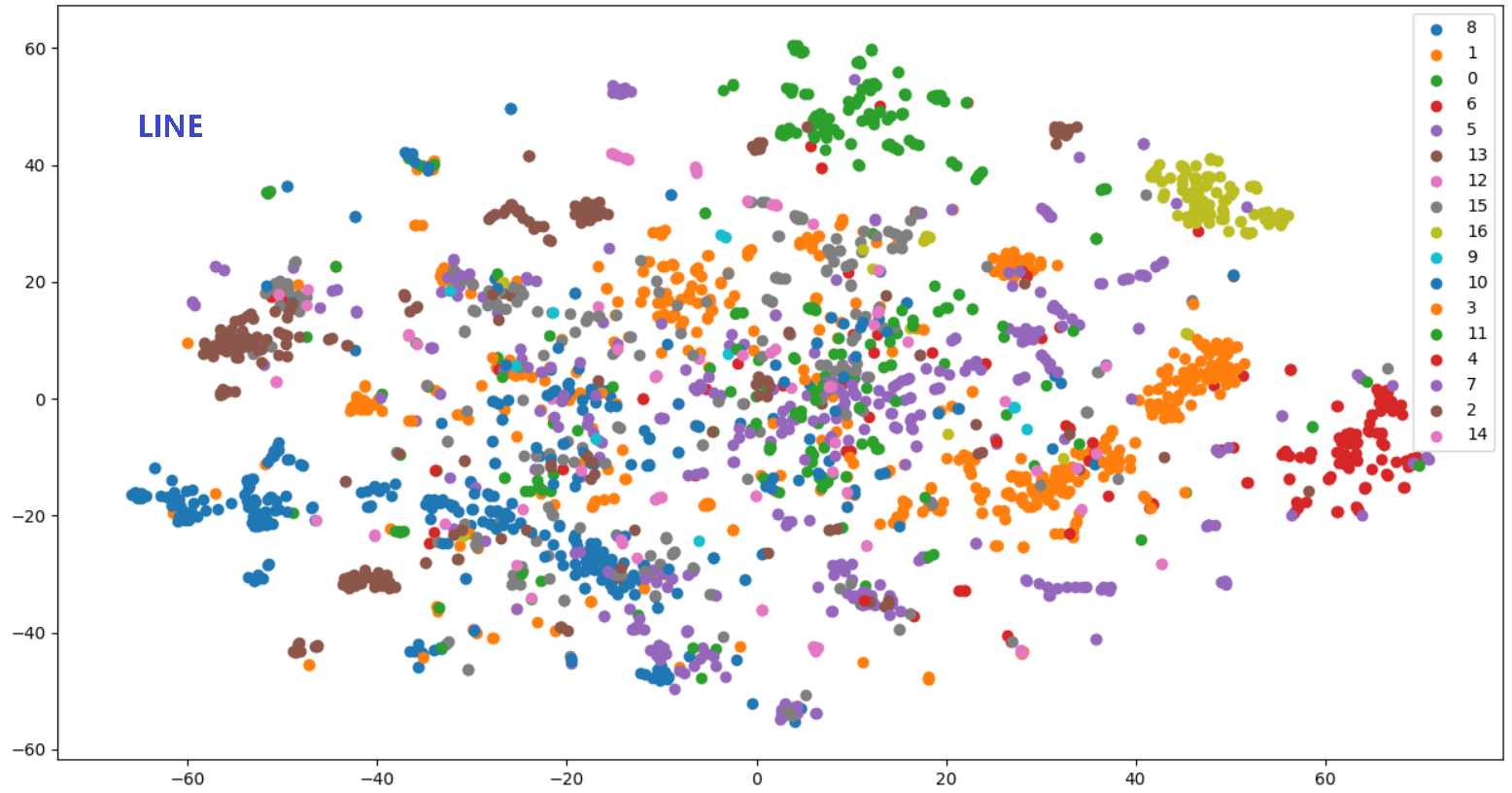
相比 DeepWalk 纯粹随机游走的序列生成方式，LINE 可以应用于有向图、无向图以及边有权重的网络，并通过将一阶、二阶的邻近关系引入目标函数，能够使最终学出的 node embedding 的分布更为均衡平滑，避免 DeepWalk 容易使 node embedding 聚集的情况发生。
3.Node2Vec---DeepWalk的进一步改进（2016）
如果单纯使用用户行为生成的物品相关图，固然可以生成物品的embedding，但是如果遇到新加入的物品，或者没有过多互动信息的长尾物品，推荐系统将出现严重的冷启动问题。**为了使“冷启动”的商品获得“合理”的初始Embedding，阿里团队通过引入了更多补充信息来丰富Embedding信息的来源，从而使没有历史行为记录的商品获得Embedding。**
生成Graph embedding的第一步是生成物品关系图，通过用户行为序列可以生成物品相关图，利用相同属性、相同类别等信息，也可以通过这些相似性建立物品之间的边，从而生成基于内容的knowledge graph。而基于knowledge graph生成的物品向量可以被称为补充信息（side information）embedding向量，当然，根据补充信息类别的不同，可以有多个side information embedding向量。
**那么如何融合一个物品的多个embedding向量，使之形成物品最后的embedding呢？最简单的方法是在深度神经网络中加入average pooling层将不同embedding平均起来，阿里在此基础上进行了加强，对每个embedding加上了权重**，如图7所示，对每类特征对应的Embedding向量，分别赋予了权重a0，a1…an。图中的Hidden Representation层就是对不同Embedding进行加权平均操作的层，得到加权平均后的Embedding向量后，再直接输入softmax层，这样通过梯度反向传播，就可以求的每个embedding的权重ai(i=0…n)。
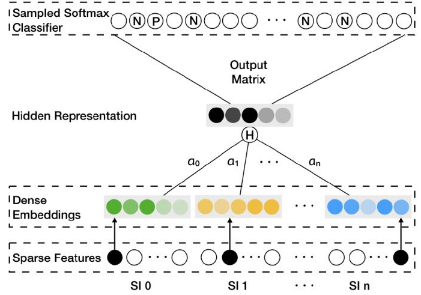
在实际的模型中，阿里采用了$e^{a_j}$而不是$a_j$作为相应embedding的权重，一是避免权重为0，二是因为$e^{a_j}$在梯度下降过程中有良好的数学性质。
阿里的EGES并没有过于复杂的理论创新，但给出一个工程性的结合多种Embedding的方法，降低了某类Embedding缺失造成的冷启动问题，是实用性极强的Embedding方法。
4.GraphSAGE（Graph SAmple and aggreGatE）
Inductive learning v.s. Transductive learning
首先我们介绍一下什么是inductive learning. 与其他类型的数据不同，图数据中的每一个节点可以通过边的关系利用其他节点的信息，这样就产生了一个问题，如果训练集上的节点通过边关联到了预测集或者验证集的节点，那么在训练的时候能否用它们的信息呢? 如果训练时用到了测试集或验证集样本的信息(或者说，测试集和验证集在训练的时候是可见的), 我们把这种学习方式叫做transductive learning, 反之，称为inductive learning. 显然，我们所处理的大多数机器学习问题都是inductive learning, 因为我们刻意的将样本集分为训练/验证/测试，并且训练的时候只用训练样本。然而，在GCN中，训练节点收集邻居信息的时候，用到了测试或者验证样本，所以它是transductive的。
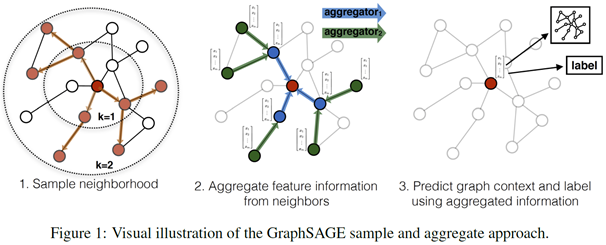
GraphSAGE是一个inductive框架，在具体实现中，训练时它仅仅保留训练样本到训练样本的边。inductive learning 的优点是可以利用已知节点的信息为未知节点生成Embedding. GraphSAGE 取自 Graph SAmple and aggreGatE, SAmple指如何对邻居个数进行采样。aggreGatE指拿到邻居的embedding之后如何汇聚这些embedding以更新自己的embedding信息。下图展示了GraphSAGE学习的一个过程：
- 对邻居采样
- 采样后的邻居embedding传到节点上来，并使用一个聚合函数聚合这些邻居信息以更新节点的embedding
- 根据更新后的embedding预测节点的标签
缺图
举个简单例子，比如一个节点的3个邻居的embedding分别为 [1,2,3,4],[2,3,4,5],[3,4,5,6] 按照每一维分别求均值就得到了聚合后的邻居embedding为 [2,3,4,5].
论文中还阐述了另外两种aggregator: LSTM aggregator 和 Pooling aggregator
其中$z_u$是节点$u$的输出embedding, $v$是节点*u*的邻居(这里邻居是广义的，比如说如果$v$和$u$在一个定长的随机游走中可达，那么我们也认为他们相邻)，是$P_n$负采样分布，$Q$是负采样的样本数量，所谓负采样指我们还需要一批不是邻$v$居的节点作为负样本，那么上面这个式子的意思是相邻节点的embedding的相似度尽量大的情况下保证不相邻节点的embedding的期望相似度尽可能小。
GraphSAGE采用了采样的机制，克服了GCN训练时内存和显存上的限制，使得图模型可以应用到大规模的图结构数据中，是目前几乎所有工业上图模型的雏形。然而，每个节点这么多邻居，采样能否考虑到邻居的相对重要性呢,Graph Attentioin Networks克服了这一困难。
5.GAT
三种注意力机制算法，都可以用来生成邻居的相对重要性
学习注意力权重（Learn attention weights）
相似性注意力（Similarity-based attention）
注意力引导的随机游走（Attention-guided walk）
首先我们对“图注意力机制”做一个数学上的定义：
定义（图注意力机制）：给定一个图中节点$v_0$ 和$v_0$的邻居节点$\left\{v_{1}, \cdots, v_{\vert\Gamma_{v_{0}}\vert}\right\} \in \Gamma_{v_{0}}$(这里的 $\Gamma_{v_{0}}$ 和GraphSAGE博文中的 $\mathcal{N}(v_0)$ 表示一个意思)。注意力机制被定义为将$\Gamma_{v_{0}}$中每个节点映射到相关性得分(relevance score)的函数$f^{\prime} :\left\{v_{0}\right\} \times \Gamma_{v_{0}} \rightarrow[0,1]$，相关性得分表示该邻居节点的相对重要性。满足：
$$\sum_{i=1}^{\vert\Gamma_{v_{0}}\vert} f^{\prime}\left(v_{0}, v_{i}\right)=1$$ (1)
学习注意力权重
核心思想是利用参数矩阵学习节点和邻居之间的相对重要性。
给定节点$v_{0}, v_{1}, \cdots, v_{\vert\Gamma_{x_{0}}\vert}$相应的特征(embedding) $\mathbf{x}_{0}, \mathbf{x}_{1}, \cdots, \mathbf{x}_{\vert\Gamma_{o^{*}}\vert}$，节点$v_0$和节点$v_j$注意力权重$\alpha_{0, j}$可以通过以下公式计算：
$$
\alpha_{0, j}=\frac{e_{0, j}}{\sum_{k \in \Gamma_{v_{0}}} e_{0, k}}
$$
其中，$e_{0,j}$表示节点$v_j$对节点$v_0$的相对重要性。在实践中，可以利用节点的属性结合softmax函数来计算,间的$e_{0,j}$相关性。比如，GAT 中是这样计算的：
$$
\alpha_{0, j}=\frac{\exp \left(\text { LeakyReLU }\left(\mathbf{a}\left[\mathbf{Wx}_{0} \| \mathbf{Wx}_{j}\right]\right)\right)}{\sum_{k \in \Gamma_{v_{0}}} \exp \left(\text { LeakyReLU }\left(\mathbf{a}\left[\mathbf{W} \mathbf{x}_{0} \| \mathbf{W} \mathbf{x}_{k}\right]\right)\right)}
$$
其中，$\mathbf{a}$ 表示一个可训练的参数向量, 用来学习节点和邻居之间的相对重要性，$\mathbf{W}$也是一个可训练的参数矩阵，用来对输入特征做线性变换，$||$表示向量拼接(concate)。
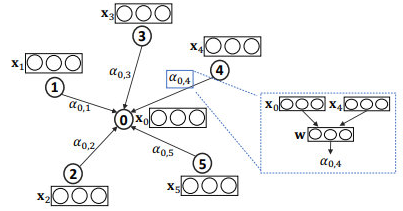
如上图，对于一个目标对象$v_0，a_{0,i}$ 表示它和邻居$v_i$的相对重要性权重。$a_{0,i}$可以根据$v_0$和$v_i$的 embedding $x_0$和$x_i$计算，比如图中$\alpha_{0, 4}$是由$x_0, x_4, \mathbf{W}, \mathbf{a}$共同计算得到的。
基于相似性的注意力
论文来自：Attention-based Graph Neural Network for Semi-supervised Learning
上面这种方法使用一个参数向量aa学习节点和邻居的相对重要性，其实另一个容易想到的点是：既然我们有节点vv的特征表示xx，假设和节点自身相像的邻居节点更加重要，那么可以通过直接计算xx之间相似性的方法得到节点的相对重要性。这种方法称为基于相似性的注意力机制，
$$
\alpha_{0, j}=\frac{\exp \left(\beta \cdot \cos \left(\mathbf{W} \mathbf{x}_{0}, \mathbf{W} \mathbf{x}_{j}\right)\right)}{\sum_{k \in \Gamma_{v_{0}}} \exp \left(\beta \cdot \cos \left(\mathbf{W} \mathbf{x}_{0}, \mathbf{W} \mathbf{x}_{k}\right)\right)}
$$
其中，$\beta$表示可训练偏差(bias)，cos函数用来计算余弦相似度，和上一个方法类似，$\mathbf{W}$是一个可训练的参数矩阵，用来对输入特征做线性变换。
这个方法和上一个方法的区别在于，这个方法显示地使用coscos函数计算节点之间的相似性作为相对重要性权重，而上一个方法使用可学习的参数$\mathbf{a}$学习节点之间的相对重要性。
注意力引导的游走法
论文来自：Graph Classification using Structural Attention
前两种注意力方法主要关注于选择相关的邻居信息，并将这些信息聚合到节点的embedding中。第三种注意力的方法的目的不同。GAM方法在输入图进行一系列的随机游走，并且通过RNN对已访问节点进行编码，构建子图embedding。时间tt的RNN隐藏状态$\mathbf{h}_{t} \in \mathbb{R}^{h}$编码了随机游走中$1, \cdots, t$ 步访问到的节点。然后，注意力机制被定义为函数 $f^{\prime} : \mathbb{R}^{h} \rightarrow \mathbb{R}^{k}$，用于将输入的隐向量$f'\left(\mathbf{h}_{t}\right)=\mathbf{r}_{t+1}$映射到一个k维向量中，可以通过比较这kk维向量每一维的数值确定下一步需要优先游走到哪种类型的节点(假设一共有k种节点类型)。下图做了形象的阐述：
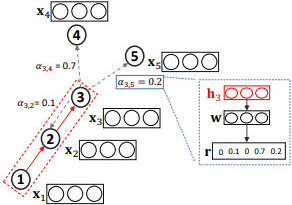
如上图，$h_3$聚合了长度$L=3$的随机游走得到的信息$\left(x_{1}, x_2, x_{3}\right)$，我们将该信息输入到排序函数中，以确定各个邻居节点的重要性并用于影响下一步游走。
6.SR-GNN
（1）背景
随着互联网上信息量的快速增长，推荐系统能够帮助用户缓解信息过载的问题，进而有效帮助用户在众多Web应用程序中（比如：搜索、电子商务、媒体流网站等）选择自己感兴趣的信息。大多数现有的推荐系统都假设一个前提：用户画像（user profile）和历史活动信息是被不断记录的。
然而实际上，在许多服务中，用户的信息可能是未知的，并且只有处于当前正在进行的会话中的用户历史行为可用。因此，在一个会话中，能对有限的行为进行建模并相应地生成推荐是非常重要的。但是在这种场景下，需要依靠丰富的user-item交互信息的传统推荐系统无法产生令人满意的推荐结果。
基于会话的推荐系统简介：
基于马尔可夫链的推荐系统：该模型基于用户上一次的行为来预测用户的下一次行为，然而由于强独立性相关假设，该模型的预测结果并不十分准确。
基于循环神经网络（RNN）的推荐系统：相比于传统的推荐问题，基于会话的推荐问题的不同点在于如何利用用户的短期会话交互信息数据来预测用户可能会感兴趣的内容。
基于会话的推荐可以建模为序列化问题，也就是基于用户的短期历史活动记录来预测下一时刻可能会感兴趣的内容并点击阅览。而深度学习中的RNN模型正是一类用于处理序列数据的神经网络。随着序列的不断推进，RNN模型中靠前的隐藏层将会影响后面的隐藏层。于是将用户的历史记录交互数据作为输入，经过多层神经网络，达到预测用户兴趣的目的。该模型也达到了令人满意的预测结果。
然而，该模型也有两处不足：
第一点就是在基于会话的推荐系统中，会话通常是匿名的且数量众多的，并且会话点击中涉及的用户行为通常是有限的，因此难以从每个会话准确的估计每个用户表示（user representation），进而生成有效推荐内容。
第二点是利用RNN来进行的建模，不能够得到用户的精确表示以及忽略了item中复杂的转换特性。
（2）SR-GNN概述
SR-GNN模型可以更好的挖掘item中丰富的转换特性以及生成准确的潜在的用户向量表示。SR-GNN模型的工作流如下：
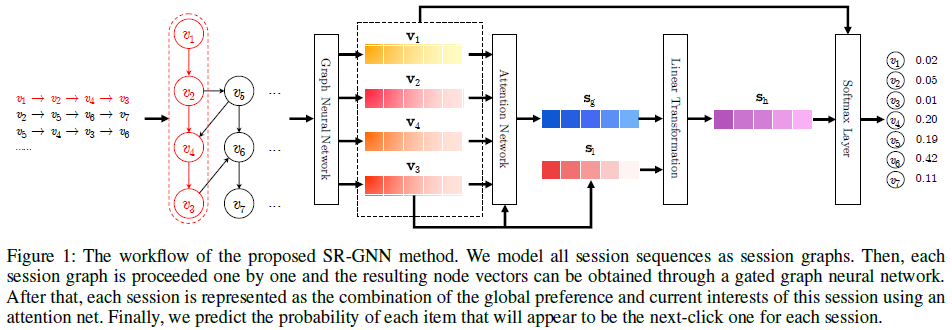
7.文本分类
图中节点的数量是单词数量+文档数量，O开头的是文档节点，其他的是词节点。图中黑线的线代表文档-词的边，灰色的表示词-词的边。R(x)表示x的embedding表示。节点的不同颜色代表文档的不同类型。
本文提出的TextGCN的初始输入向量是词和文档全部用one-hot编码表示。文档-词的边基于词在文档中的出现信息，使用TF-IDF作为边的权重。词-词的连边基于词的全局词共现信息。词共现信息使用一个固定大小的滑动窗口在语料库中滑动统计词共现信息，然后使用点互信息（PMI）计算两个词节点连线的权重。具体如下：
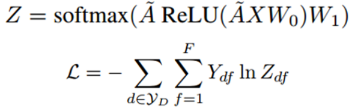
结论：Text GCN可以捕获文档和词的关系以及全局词共现信息，文档节点的标签信息可以通过他们的邻居节点传递，传递给其他的单词和文档。在情感分类任务上（MR语料）上Text GCN没有表现出优于其他基准模型的结果，主要是因为GCN忽略了词序信息，这在情感分类当中时非常有用的。
实验还证明了参数的敏感性。在Text GCN中，窗口大小和第一层GCN输出的向量维度大小的选择都对结果有影响，较小的窗口不能得到有效地全局词共现信息，太大的窗口会使得本来关系并不密切的两个节点之间产生连边。
在本文的实验中，Text GCN可以有很好的文本分类结果，但是不能快速生成embedding，也不能为新的文本作分类。在未来的工作中可以引入归纳机制，注意力机制，发展无监督的text GCN框架。
参考文献：
【1】Graph Embedding：深度学习推荐系统的基本操作
【2】Graph Convolutional Networks for Text Classification解析
