3(2).特征选择---包装法

1. 前向搜索

　　每次增量地从剩余未选中的特征选出一个加入特征集中，待达到阈值或者 时，从所有的  中选出错误率最小的。过程如下：

• 初始化特征集  为空。
• 扫描  从  到 
• 如果第  个特征不在  中，那么特征  和 放在一起作为  (即  )。
• 在只使用  中特征的情况下，利用交叉验证来得到  的错误率。
• 从上步中得到的  个  中选出错误率最小的  ,更新  为  。
• 如果  中的特征数达到了  或者预定的阈值（如果有的话），
• 那么输出整个搜索过程中最好的 ；若没达到，则转到 2，继续扫描。

2. 后向搜索

　　既然有增量加，那么也会有增量减，后者称为后向搜索。先将  设置为  ，然后每次删除一个特征，并评价，直到达到阈值或者为空，然后选择最佳的  。

　　这两种算法都可以工作，但是计算复杂度比较大。时间复杂度为

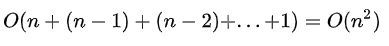
3. 递归特征消除法

 　　递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下：

?

1 2 3 4 5 6 7

from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression   #递归特征消除法，返回特征选择后的数据 #参数estimator为基模型 #参数n_features_to_select为选择的特征个数 RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)

 

举例：使用一个基模型来进行多轮训练，经过多轮训练后，保留指定的特征数。

+ View Code?

#首先导入数据到data变量中

import pandas

data=pandas.read_csv('路径.csv')

 

#接着，我们使用RFE类，在estimator中，

#把我们的基模型设置为线性回归模型LinearRegression,

#然后在把我们要选择的特征数设置为2，

#接着就可以使用这个rfe对象，把自变量和因变量传入fit_transform方法，

#即可得到我们需要的特征值

from sklearn.feature_selection import RFE

from sklearn.linear_model import LinearRegression

 

feature =data[['月份','季度','广告推广费','注册并投资人数']]

 

rfe =RFE(

    estimator=LinearRegression(),

    n_features_to_select=2

)

sFeature = rfe.fit_transform(

    feature,

    data['销售金额']

)

 

#同理，我们要想知道这两个自变量的名字，

#使用get_support方法，即可得到对应的列名

rfe.get_support()