2(1).数据预处理方法

posted @ 2019-07-06 10:53 nxf_rabbit75 阅读(5026) 评论(1) 编辑收藏举报

分类: 特征工程

undefined

（一）数值特征

数值特征（numerical feature），可以是连续的（continuous），也可以是离散的（discrete），一般表示为一个实数值。

例：年龄、价格、身高、体重、测量数据。

不同算法对于数值特征的处理要求不同。下文中的一些数据处理方法，因为是针对某一特征列的单调变换，所以不会对基于决策树的算法（随机森林、gbdt）产生任何影响。一般而言，决策树类算法不需要预处理数值特征。

一、数值特征缩放

适用场景：

基于距离的算法
算法用到了梯度下降

1.Rescaling(最小最大标准化/归一化,不免疫outlier）

（1）将训练集中某一列数值特征（假设是第i列）的值缩放到0和1之间

适用场景：

如果对输出结果范围有要求，用归一化
如果数据较为稳定，不存在极端的最大最小值，用归一化

缺点：这种方法有个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

参考：

from sklearn.preprocessing import MinMaxScaler
 
#初始化一个scaler对象
scaler = MinMaxScaler()
 
#调用scaler的fit_transform方法，把我们要处理的列作为参数传进去
data['标准化后的A列数据'] = scaler.fit_transform(data['A列数据'])

（2）要重新缩放任意值集[a,b]之间的范围，公式将变为：

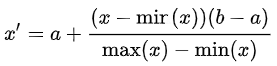
a，b是最小-最大值

2.Mean normalization(均值归一化，不免疫outlier)

将训练集中某一列数值特征（假设是第i列）的值缩放到[-1,1]零均值之间

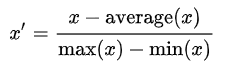
适用场景：

矩阵分解

参考：

3.Standardization(标准化/z-score标准化，不免疫outlier）

将训练集中某一列数值特征（假设是第i列）的值缩放成均值为0，方差为1的状态。

适用场景：

SVM、LR、神经网络
如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响

参考：

sklearn.preprocessing.scale
sklearn.preprocessing.StandardScaler（两个基本一样，但一般用这个就ok了，比较高级、方法比较齐全）

# 方法1
from sklearn.proprocessing import scale
df_train['feature'] = scale(df_train['feature'])
 
# 方法2
# 一般会把train和test集放在一起做标准化，或者在train集上做标准化后，用同样的标准化器去标准化test集，此时可以用scaler
from sklearn.proprocessing import StandardScaler
scaler = StandardScaler().fit(df_train)
scaler.transform(df_train)
scaler.transform(df_test)

4.scaling to unit length(缩放到单位长度，不免疫outlier)

在机器学习中广泛使用的另一种选择是缩放特征向量的分量，使得完整向量具有长度1。这通常意味着将每个组件除以向量的欧几里德长度：

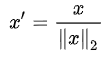
使用场景：

在一些应用中（例如直方图特征），使用特征向量的L1范数（即曼哈顿距离，城市块长度或出租车几何）可能更实际。如果在以下学习步骤中将标量度量用作距离度量，则这尤其重要。

参考：

1	`sklearn.preprocessing.Normalizer(norm=’l2’, copy=True)`

参数：

norm：'l1','l2',或'max',可选，默认='l2'
copy：boolean，可选，默认=True

5.绝对值标准化（不免疫outlier）

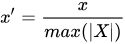
　　专为稀疏数据而生。将每个要素缩放到[-1,1]范围，它不会移动/居中数据，因此不会破坏任何稀疏性。该估计器单独地缩放每个特征，使得训练集中的每个特征的最大绝对值将是1.0。该缩放器也可以应用于稀疏CSR或CSC矩阵

参考：

sklearn.preprocessing.maxabs_scale(X, axis=0, copy=True)
sklearn.preprocessing.MaxAbsScaler(copy=True)（这两者的关系同上）

6.鲁棒性标准化（免疫outlier）

　　专为异常值而生。标准差标准化（第一种，最常用的那种）对数据中出现的异常值处理能力不佳，因此诞生了robust_scale，这种不怕异常值扰动的数据缩放法。此Scaler根据分位数范围（默认为IQR：Interquartile Range）删除中位数并缩放数据。 IQR是第1四分位数（第25个分位数）和第3个四分位数（第75个分位数）之间的范围。

参考：

7.对数/平方根缩放：

适用场景：对数缩放对于处理长尾分布且取值为正数的数值变量非常有效，它将大端长尾压缩为短尾，并将小端进行延伸，平方根或者对数变换是幂变换的特例，在统计学中都称为方差稳定的变换

举例：对数缩放

1 2	`import` `numpy as np` `data["log_feature1"]` `=` `np.log10(data["feature1"])`

8.box-cox变换

适用场景：基于极大似然法的幂转换，其作用是让分布在不丢失信息的前提下，具有更好的性质（独立性、方差齐性、正态性等），以便得到更好的模型。

要求：

　　Box-Cox变换的要求是数据要大于0，否则无法变换，解决的办法是加一个常数，把数据变成正数；

　　变换后，必须再做正态性检验，确认变换的有效性；

求 $\lambda$ ：假设经过转换后的因变量就是服从正态分布的，然后画出关于 $\lambda$ 的似然函数，似然函数值最大的时候 $\lambda$ 的取值就是这里需要确定的值。

9.上下界截断：

clipping：可以用pandas dataframe的.clip(low, upper)方法，把特征值的取值限制在一定范围内
?
1
2
data.ix[data['feature1']>10,'feature1'] = 10
data.ix[data['feature2']<-20,'feature2'] = -20

三、数值特征离散化

这对于决策树类型的模型没太多意义

1.二值化

设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0；默认阈值为0时，只有正值映射到1。

1	`class` `sklearn.preprocessing.Binarizer(threshold=0.0, copy=True)`

参数：

threshold：float，可选，默认=0.0，对于稀疏矩阵上的操作，阈值可能不小于0。
copy：boolean，可选，默认=True

举例：

from sklearn.datasets import load_iris
import pandas as pd
from sklearn.preprocessing import Binarizer
 
X,y = load_iris(return_X_y=True)    
df_X = pd.DataFrame(X,columns=list("ABCD"))
bn = Binarizer(threshold=5.843333)
df_X["A"] = bn.transform(df_X["A"].values.reshape(-1,1))

2.分桶

（1）等宽/非等宽分桶

　　如商品的评论次数、年龄

参考：

pandas.cut(x, bins, right=True, labels=None, retbins=False, precision=3, include_lowest=False, duplicates='raise')
当bins为int型数字时，会生成等宽的bin；当bins=标量序列时，为用户自定义bin的区间

（2）等频率分桶

　　如果数值变量的取值存在很大间隔时,有些桶里没有数据,可以基于数据的分布进行分桶,.

将相同数据的记录放进每个区间，先求分位数，再用cut函数

①dataframe结构

dataframe.describe(percentiles=w)来计算分位数

w=[ i/k for i in range(k+1)]
w=data.describe (percentiles=w) [ 4:4+k+1] #取几个分位数的值作为不等长列表，用于cut函数
d2=pd.cut(data,w,labels=range(k))

②列表、数组结构

#用np.percentile(data,百分比）来求
temp=[ i/k*100 for i in range(k+1)]
w=[]
for item in temp:
    w.append(np.percentile(data,item))
d3=pd.cut(data,w,labels=range(k))

参考：

pandas.qcut(x, q, labels=None, retbins=False, precision=3, duplicates='raise')

（3）一维聚类离散化

先聚类（如k-means），然后对每一类的连续值进行标记

①k-means求聚类中心，并排序，将相邻两项的中点作为边界点，把首末边界点加上，整合成w列表

②cut函数

from sklearn.cluster import KMeans
kmodel=KMeans(n_clusters=k)  #k为聚成几类
kmodel.fit(data.reshape(len(data),1))) #训练模型
c=pd.DataFrame(kmodel.cluster_centers_) #求聚类中心
c=c.sort_values(by=’列索引') #排序　　
w=pd.rolling_mean(c,2).iloc[1:] #用滑动窗口求均值的方法求相邻两项求中点，作为边界点
w=[0] +list(w[0] + [ data.max() ]  #把首末边界点加上
d3= pd.cut(data,w,labels=range(k)) #cut函数

四、缺失值处理

数值特征缺失值处理

五、特征交叉

1. 数值特征的简单变换

单独特征列乘以一个常数（constant multiplication）或者加减一个常数：对于创造新的有用特征毫无用处；只能作为对已有特征的处理。
任何针对单独特征列的单调变换（如对数）：不适用于决策树类算法。对于决策树而言， $X、X^3、X^5$ 之间没有差异， $|X|、X^2、X^4$ 之间没有差异，除非发生了舍入误差。
线性组合（linear combination）：仅适用于决策树以及基于决策树的ensemble（如gradient boosting, random forest），因为常见的axis-aligned split function不擅长捕获不同特征之间的相关性；不适用于SVM、线性回归、神经网络等。

多项式特征（polynomial feature）：

sklearn.preprocessing.PolynomialFeatures - scikit-learn 0.18.1 documentation。

捕获特征之间的相关性, 使用sklearn.preprocessing.PolynomialFeatures来进行特征的构造。它是使用多项式的方法来进行的，如果有a，b两个特征，那么它的2次多项式为（1,a,b,a^2,ab, b^2），这个多项式的形式是使用poly的效果。

PolynomialFeatures有三个参数
degree：控制多项式的度
interaction_only：默认为False，如果指定为True，那么就不会有特征自己和自己结合的项，上面的二次项中没有a^2和b^2。

from sklearn.datasets import load_iris
import pandas as pd
X,y = load_iris(return_X_y=True)    
df_X = pd.DataFrame(X,columns=list("ABCD"))
 
from sklearn.preprocessing import PolynomialFeatures
 
pnf = PolynomialFeatures(degree=2,interaction_only=True)
temp  = pnf.fit_transform(df_X[["A","B"]].values)
for i,column in enumerate(list("EFGH")):
    df_X[column] = temp[:,i]

比例特征（ratio feature）： $X_1/X_2$
绝对值（absolute value）
$max(X_1,X_2)，min(X_1,X_2)，X_1xorX_2$

2. 类别特征与数值特征的组合

用N1和N2表示数值特征，用C1和C2表示类别特征，利用pandas的groupby操作，可以创造出以下几种有意义的新特征：（其中，C2还可以是离散化了的N1）

median(N1)_by(C1)  \\ 中位数
mean(N1)_by(C1)  \\ 算术平均数
mode(N1)_by(C1)  \\ 众数
min(N1)_by(C1)  \\ 最小值
max(N1)_by(C1)  \\ 最大值
std(N1)_by(C1)  \\ 标准差
var(N1)_by(C1)  \\ 方差
freq(C2)_by(C1)  \\ 频数

freq(C1) \\这个不需要groupby也有意义

View Code

仅仅将已有的类别和数值特征进行以上的有效组合，就能够大量增加优秀的可用特征。

将这种方法和线性组合等基础特征工程方法结合（仅用于决策树），可以得到更多有意义的特征，如：

N1 - median(N1)_by(C1)
N1 - mean(N1)_by(C1)

View Code

3.用基因编程创造新特征

Welcome to gplearn’s documentation!

基于genetic programming的symbolic regression，具体的原理和实现参见文档。目前，python环境下最好用的基因编程库为gplearn。基因编程的两大用法：

转换（transformation）：把已有的特征进行组合转换，组合的方式（一元、二元、多元算子）可以由用户自行定义，也可以使用库中自带的函数（如加减乘除、min、max、三角函数、指数、对数）。组合的目的，是创造出和目标y值最“相关”的新特征。这种相关程度可以用spearman或者pearson的相关系数进行测量。spearman多用于决策树（免疫单特征单调变换），pearson多用于线性回归等其他算法。
回归（regression）：原理同上，只不过直接用于回归而已。

4. 用决策树创造新特征

在决策树系列的算法中（单棵决策树、gbdt、随机森林），每一个样本都会被映射到决策树的一片叶子上。因此，我们可以把样本经过每一棵决策树映射后的index（自然数）或one-hot-vector（哑编码得到的稀疏矢量）作为一项新的特征，加入到模型中。

具体实现：apply()以及decision_path()方法，在scikit-learn和xgboost里都可以用。

六、非线性编码

七、行统计量

DataFrame.nunique()，DataFrame.count

（二）类别特征

一、编码

1.one-hot

　　如果类别特征本身有顺序（例：优秀、良好、合格、不合格），那么可以保留单列自然数编码。如果类别特征没有明显的顺序（例：红、黄、蓝），则可以使用one-hot编码：

作用：将类别变量转换为机器学习算法容易处理的形式
为什么one-hot编码可以用来处理非连续(离散)特征？
- 在使用one-hot编码中，我们可以将离散特征的取值扩展到欧式空间，在机器学习中，我们的研究范围就是在欧式空间中，首先这一步，保证了能够适用于机器学习中；另外对于one-hot处理的离散的特征的某个取值也就对应了欧式空间的某个点.
怎么用？

sklearn.preprocessing.OneHotEncoder(n_values=None, categorical_features=None, categories=None, drop=None, sparse=True, dtype=<class ‘numpy.float64’>, handle_unknown=’error’)

View Code
如果需要修改编码后的列名

categorical_features =['cardIndex','is_abnormal']
dummies = pd.get_dummies(data,columns=categorical_features)
dummies = dummies.add_prefix("{}_".format('cardIndex'))
data.drop('animal',axis=1,inplace=True)
data = data .join(dummies)
data