标准化和归一化
一、是什么？
1. 归一化
是为了将数据映射到0~1之间，去掉量纲的过程，让计算更加合理，不会因为量纲问题导致1米与100mm产生不同。
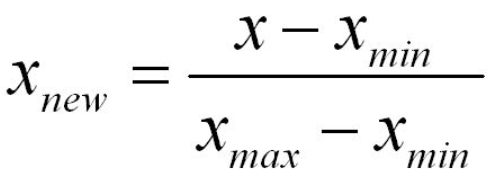
归一化是线性模型做数据预处理的关键步骤，比如LR，非线性的就不用归一化了。
归一化就是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。
缺点：这种方法有个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。
另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景
2. z-标准化
消除分布产生的度量偏差，例如：班级数学考试，数学成绩在90-100之间，语文成绩在60-100之间，那么，小明数学90，语文100，小花数学95，语文95，如何评价两个综合成绩好坏的数学处理方式。
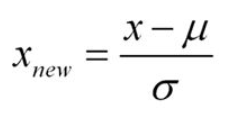
二、怎么选？
1. 标准化
- 标准化更好保持了样本间距。当样本中有异常点时，归一化有可能将正常的样本“挤”到一起去。比如三个样本，某个特征的值为1,2,10000，假设10000这个值是异常值，用归一化的方法后，正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的，那么，当我们用梯度下降来做分类模型训练时，模型会需要更长的时间收敛，因为将样本分开需要更大的努力！而标准化在这方面就做得很好，至少它不会将样本“挤到一起”。
- 标准化更符合统计学假设：对一个数值特征来说，很大可能它是服从正态分布的。标准化其实是基于这个隐含假设，只不过是略施小技，将这个正态分布调整为均值为0，方差为1的标准正态分布而已。
（1）逻辑回归必须要进行标准化吗？
答案：这取决于我们的逻辑回归是不是用正则。
如果你不用正则，那么，标准化并不是必须的，如果你用正则，那么标准化是必须的。（暗坑3）
为什么呢？
因为不用正则时，我们的损失函数只是仅仅在度量预测与真实的差距，加上正则后，我们的损失函数除了要度量上面的差距外，还要度量参数值是否足够小。而参数值的大小程度或者说大小的级别是与特征的数值范围相关的。举例来说，我们用体重预测身高，体重用kg衡量时，训练出的模型是： 身高 = 体重*x ，x就是我们训练出来的参数。
当我们的体重用吨来衡量时，x的值就会扩大为原来的1000倍。
在上面两种情况下，都用L1正则的话，显然对模型的训练影响是不同的。
假如不同的特征的数值范围不一样，有的是0到0.1，有的是100到10000，那么，每个特征对应的参数大小级别也会不一样，在L1正则时，我们是简单将参数的绝对值相加，因为它们的大小级别不一样，就会导致L1最后只会对那些级别比较大的参数有作用，那些小的参数都被忽略了。
如果你回答到这里，面试官应该基本满意了，但是他可能会进一步考察你，如果不用正则，那么标准化对逻辑回归有什么好处吗？
答案是有好处，进行标准化后，我们得出的参数值的大小可以反应出不同特征对样本label的贡献度，方便我们进行特征筛选。如果不做标准化，是不能这样来筛选特征的。
答到这里，有些厉害的面试官可能会继续问，做标准化有什么注意事项吗？
最大的注意事项就是先拆分出test集，不要在整个数据集上做标准化，因为那样会将test集的信息引入到训练集中，这是一个非常容易犯的错误！
举例：简单的预测房价的线性回归模型：
有一组关于房价和房子变量的数据集，通过房子的面积，房间数量，房子的层数来预测房价。
占地面积1800尺，房间数量3间，房子层数2层-> 房价?；为了方便对比，我们分别看一下标准化前和标准化后的模型输出分布是怎么样的。
可以看出，标准化前后变量的系数不同，误差不同，但是R平方，和变量的t值是相同的。
现在我们来预测一个1590尺，3个卧室，3层的房屋
我们发现预测出来的房价是一样的。
这时你一定会想，既然结果都一样，做不做标准化，都一样嘛。说到这里，我们再看一下，建模时寻找最优解的时间吧。
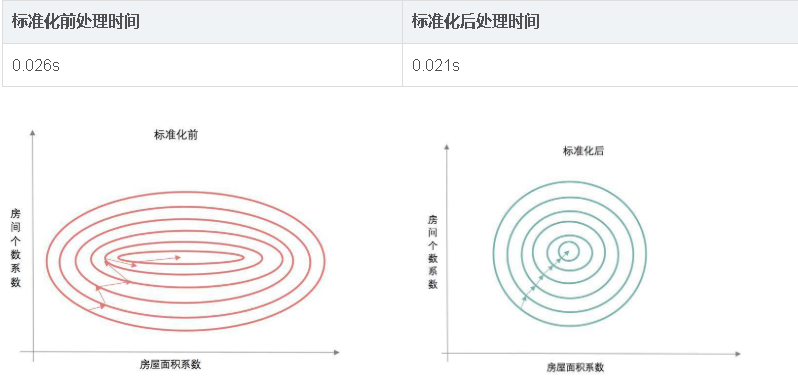
为什么标准化后的建模时间会短呢？这时候就要说起寻找系数最优解-梯度下降法。
标准化前，由于变量的单位相差很大，导致了椭圆型的梯度轮廓。标准化后，把变量变成统一单位，产生了圆形轮廓。由于梯度下降是按切线方向下降，所以导致了系统在椭圆轮廓不停迂回地寻找最优解，而圆形轮廓就能轻松找到了。
还有一种比较极端的情况，有时没做标准化，模型始终找不到最优解，一直不收敛。
（2）PCA需要标准化吗？
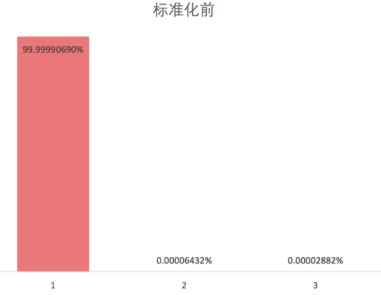
我们再来看一下，如果将预测房价的变量，用PCA方法来降维，会不会对结果产生影响。
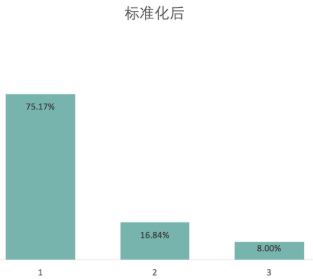
我们看出在标准化前，用一个成分就能解释99%的变量变化，而标准化后一个成分解释了75%的变化。 主要原因就是在没有标准化的情况下，我们给了居住面积过大权重，造成了这个结果。
（3）Kmeans，KNN需要标准化吗?
Kmeans，KNN一些涉及到距离有关的算法，或者聚类的话，都是需要先做变量标准化的。
举例：我们将3个城市分成两类，变量有面积和教育程度占比；三个城市分别是这样的：
城市A，面积挺大，但是整天发生偷盗抢劫，教育程度低；
城市B，面积也挺大，治安不错，教育程度高；
城市C，面积中等，治安也挺好，教育程度也挺高；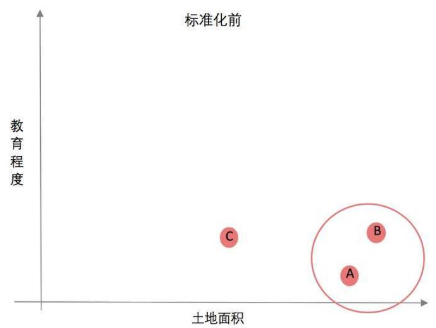
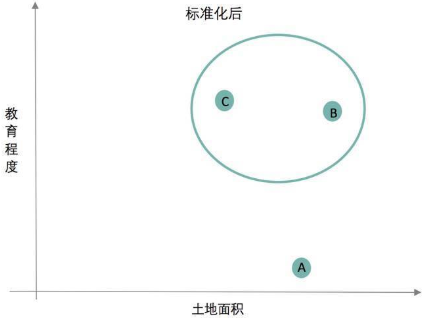
我们如果不做标准化，直接做聚类模型的话，A城市和B城市分在一块儿了，你想想，一个治安挺好的城市和一个整体偷盗抢劫城市分在一起，实在是有点违反常理。
总结：
在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，Z-score standardization表现更好
基于树的模型不需要标准化；
用到正则的线性模型一定要标准化，没用到正则的线性模型不一定要标准化， 但标准化可以加快收敛；
基于距离或聚类需要先做标准化，如KNN、kmeans
PCA最好先做标准化
2. 归一化
模型算法里面有没关于对距离的衡量，没有关于对变量间标准差的衡量。比如decision tree 决策树，他采用算法里面没有涉及到任何和距离等有关的，所以在做决策树模型时，通常是不需要将变量做标准化的。
在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。有时候，我们必须要特征在0到1之间，此时就只能用归一化。有种svm可用来做单分类，里面就需要用到归一化。
三、怎么用？
#导入数据到data变量中
import pandas
data = pandas.read_csv('路径.csv')
#（一）Min-Max 标准化
from sklearn.preprocessing import MinMaxScaler
#初始化一个scaler对象
scaler = MinMaxScaler()
#调用scaler的fit_transform方法，把我们要处理的列作为参数传进去
data['标准化后的A列数据'] = scaler.fit_transform(data['A列数据'])
data['标准化后的B列数据'] = scaler.fit_transform(data['B列数据'])
#（二）Z-Score标准化 （可在scale中直接实现）
from sklearn.preprocessing import scale
data['标准化后的A列数据'] = scale(data['A列数据'])
data['标准化后的B列数据'] = scale(data['B列数据'])
# (三) Normalizer归一化
from sklearn.preprocessing import Normalizer
scaler = Normalizer()
#归一化可以同时处理多个列，所以[0]第一个进行赋值
data['归一化后的A列数据'] = scaler.fit_transform(data['A列数据'])[0]
data['归一化后的B列数据'] = scaler.fit_transform(data['B列数据'])[0]
参考文献：
【1】关于数据建模变量标准化
