ROC曲线，AUC面积

　　AUC(Area under Curve)：Roc曲线下的面积，介于0.1和1之间。Auc作为数值可以直观的评价分类器的好坏，值越大越好。

　　首先AUC值是一个概率值，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。

1. 什么是ROC曲线？

　　ROC曲线是Receiver operating characteristic curve的简称，中文名为“受试者工作特征曲线”。ROC曲线源于军事领域，横坐标为假阳性率（False positive rate，FPR）,纵坐标为真阳性率（True positive rate，TPR）.

假阳性率 FPR = FP/N ---N个负样本中被判断为正样本的个数占真实的负样本的个数 

真阳性率 TPR = TP/P ---P个正样本中被预测为正样本的个数占真实的正样本的个数

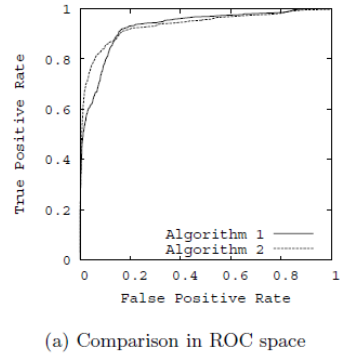
2. 如何绘制ROC曲线？

　　ROC曲线是通过不断移动分类器的“截断点”来生成曲线上的一组关键点的，“截断点”指的就是区分正负预测结果的阈值。

　　通过动态地调整截断点，从最高的得分开始，逐渐调整到最低得分，每一个截断点都会对应一个FPR和TPR,在ROC图上绘制出每个截断点对应的位置，再连接所有点就得到最终的ROC曲线。

　　ROC曲线一定程度上可以反映分类器的分类效果，但是不够直观，我们希望有这么一个指标，如果这个指标越大越好，越小越差，于是，就有了AUC。AUC实际上就是ROC曲线下的面积。AUC直观地反映了ROC曲线表达的分类能力。

  • AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
  • 0.5<AUC<10，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
  • AUC=0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
  • AUC<0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测，因此不存在 AUC<0.5AUC<0.5 的情况。

3. 如何计算AUC？

（1）适合数据量少

　　AUC是一个模型评价指标，只能用于二分类模型的评价，对于二分类模型，还有很多其他评价指标，比如logloss，accuracy，precision。为什么AUC和logloss比accuracy更常用呢？因为很多机器学习的模型对分类问题的预测结果都是概率，如果要计算accuracy，需要先把概率转化成类别，这就需要手动设置一个阈值，如果一个样本的预测概率高于这个预测，就把这个样本放进一个类别里面，低于这个阈值，放进另一个类别里面。所以这个阈值很大程度上影响了accuracy的计算，使用AUC或logloss可以避免把预测概率转换成类别。

　　AUC是Area under curve的首字母缩写，从字面上理解，就是ROC曲线下的面积大小，该值能够量化地反映基于ROC曲线衡量出的模型性能。由于ROC曲线一般都处于y=x这条直线的上方（如果不是的话，只要把模型预测的概率反转成1-p就可以得到一个更好的分类器），所以AUC的取值一般在0.5-1之间。AUC越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。

 

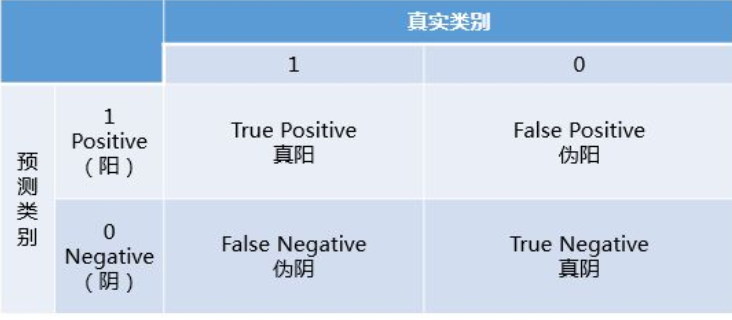
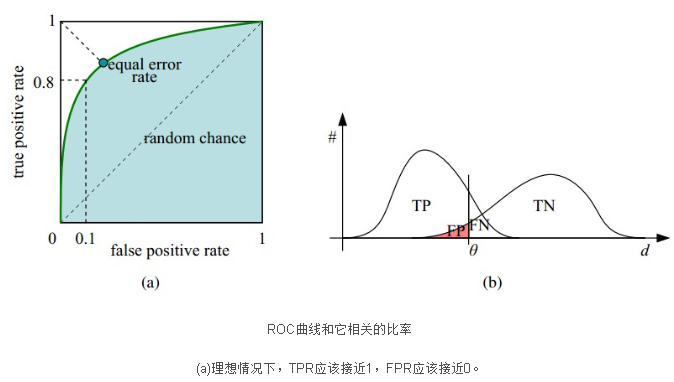
举例：5个样本，真实的类别（标签）是

y 1 1 0 0 1
p 0.5 0.6 0.55 0.4 0.7

　　如文章一开始多说，我们需要选定阈值才能把概率转化为类别，选定不同的阈值会得到不同的结果。如果我们选定的阈值为0.1，那5个样本被分进1的类别，如果选定0.3，结果仍然一样。如果选了0.45作为阈值，那么只有样本4被分进0，其余都进入1类。一旦得到了类别，我们就可以计算相应的真、伪阳性率，当我们把所有计算得到的不同真、伪阳性率连起来，就画出了ROC曲线。

python代码如下：

from sklearn import metrics
def aucfun(act,pred):
    fpr,tpr,thresholds = metrics.roc_curve(act,pred,pos_label=1)
    return metrics.auc(fpr,tpr)

（2）适合数据量大，时间复杂度O(N*M)

　　一个关于AUC的很有趣的性质是，它和Wilcoxon-Mann-Witney Test是等价的。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。有了这个定义，我们就得到了另外一中计 算AUC的办法：得到这个概率。我们知道，在有限样本中我们常用的得到概率的办法就是通过频率来估计。这种估计随着样本规模的扩大而逐渐逼近真实值。这和上面的方法中，样本数越多，计算的AUC越准确类似，也和计算积分的时候，小区间划分的越细，计算的越准确是同样的道理。具体来说就是统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数（即n=M+N） 

（3）适合数据量大，时间复杂度O(M+N)

　　第三种方法实际上和上述第二种方法是一样的，但是复杂度减小了。它也是首先对score从大到小排序，然后令最大score对应的sample 的rank为n，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N。

详细解释如下： 随机抽取一个样本，对应每一潜在可能值X都对应有一个判定位正样本的概率P。

　　对一批已知正负的样本集合进行分类。

　　按概率从高到矮排序，对于正样本中概率最高的，排序为rank_1，比它概率小的有M-1个正样本（M为正样本个数），（rank_1-M）个负样本。

　　正样本概率第二高的，排序为rank_2，比它概率小的有M-2个正样本，（rank_2-M+1）个负样本。

　　以此类推，正样本中概率最小的，排序为rank_M，比它概率小的有0个正样本，rank_M-1个负样本。

　　总共有M*N个正负样本对（N为负样本个数）。把所有比较中，正样本概率大于负样本概率的例子都算上，得到公式(rank_1-M+rank_2-M+1...+rank_M-1)/(M*N)就是正样本概率大于负样本概率的可能性了。化简后得：【离散情况下】

 

 

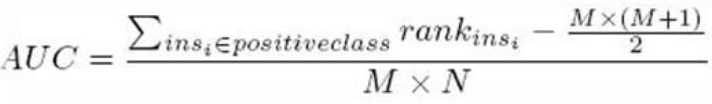
4. ROC曲线相比P-R曲线有什么特点？

　　当正负样本的分布发生变化时，ROC曲线的形状能够基本保持不变，而P-R曲线的形状一般会发生较剧烈的变化。ROC能够尽量降低不同测试集带来的干扰，更加客观的衡量模型本身的性能。如果研究者希望更多地看到模型在特定数据集上的表现，P-R曲线能够更直观地反映其性能。

 

5. ROC实现

（1）pandas实现roc

随机生成样本和结果

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline
import warnings
warnings.filterwarnings("ignore")

#测试样本数量
parameter = 30

#随机生成结果集
data = pd.DataFrame(index=range(0,parameter),columns=('probability','label'))
data['label'] = np.random.randint(0,2,size=len(data))
data['probability'] = np.random.choice(np.arange(0.1,1.0,0.1),len(data['probability']))
data.columns　　

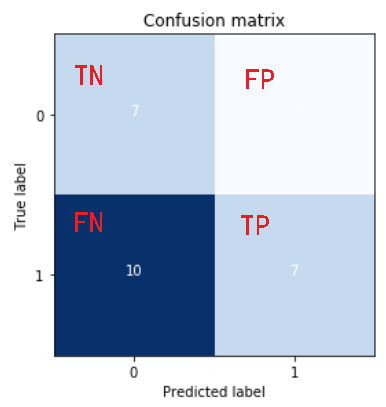
计算混淆矩阵

#计算混淆矩阵
cm = np.arange(4).reshape(2,2)
cm[0,0] = len(data.query('label==0 and probability<0.5')) #TN
cm[0,1] = len(data.query('label==0 and probability>=0.5')) #FP
cm[1,0] = len(data.query('label==1 and probability<0.5')) #FN
cm[1,1] = len(data.query('label==1 and probability>=0.5')) #TP
cm

 画出混淆矩阵

import itertools
classes = [0,1]
plt.figure()
plt.imshow(cm,interpolation='nearest',cmap=plt.cm.Blues)
plt.title('Confusion matrix')
tick_marks=np.arange(len(classes))
plt.xticks(tick_marks,classes,rotation=0)
plt.yticks(tick_marks,classes)
thresh = cm.max()/2
for i,j in itertools.product(range(cm.shape[0]),range(cm.shape[1])):
    plt.text(j,i,cm[i,j],horizontalalignment='center',color = 'white' if cm[i,j]>thresh else 'black')
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')

　

　　ROC曲线是一系列threshold下的（FPR，TPR）数值点的连线。此时的threshold的取值分别为测试数据集中各样本的预测概率。但，取各个概率的顺序是从大到小的。

#按预测概率从大到小的顺序排序
data.sort_values('probability',inplace=True,ascending=False)
data.head()

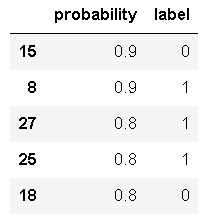
阈值分别取0.9,0.9,0.8,0.8,...比如,当threshold=0.9（第三个0.9）,两个“0”预测错误，一个“1”预测正确，

FPR=1/13,TPR=1/17

#计算全部概率值下的FPR，TPR
TFRandFPR = pd.DataFrame(index=range(len(data)),columns=('TP','FP'))

for j in range(len(data)):
    data1 = data.head(n=j+1)
    FP=len(data1[data1['label']==0] [data1['probability']>=data1.head(len(data1))['probability']])/float(len(data[data['label']==0]))
    TP=len(data1[data1['label']==1] [data1['probability']>=data1.head(len(data1))['probability']])/float(len(data[data['label']==1]))
    TFRandFPR.iloc[j] = [TP,FP]


from sklearn.metrics import auc
AUC = auc(TFRandFPR['FP'],TFRandFPR['TP'])

plt.scatter(x=TFRandFPR['FP'],y=TFRandFPR['TP'],label='(FPR,TPR)',color='k')
plt.plot(TFRandFPR['FP'],TFRandFPR['TP'],'k',label='AUC=%0.2f'%AUC)
plt.legend(loc='lower right')

plt.title('Receiver Operating Characteristic')
plt.plot([(0,0),(1,1)],'r--')
plt.xlim([-0.01,1.01])
plt.ylim([-0.01,01.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()

　

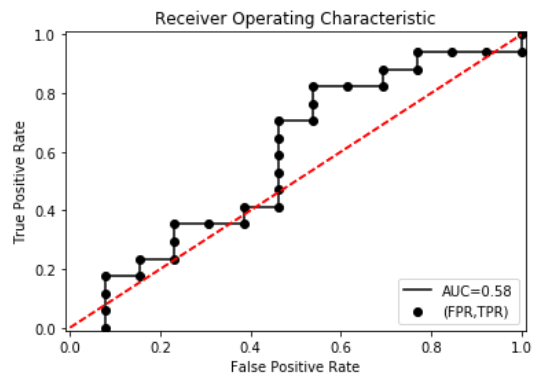
 　　在此例子中AUC=0.58，AUC越大，说明分类效果越好。

　

（2）直接计算直方图面积

def roc_auc(labels,preds,n_bins=1500):
    pos_len = sum(labels)
    neg_len = len(labels) - pos_len
    total_case = pos_len * neg_len
    pos_hist = [0 for i in range(n_bins)]
    neg_hist = [0 for i in range(n_bins)]
    bin_width = 1.0 / float(n_bins)
    for i in range(len(labels)):
        nth_bin = int(preds[i]/bin_width)
        if labels[i]==1:
            pos_hist[nth_bin] += 1
        else:
            neg_hist[nth_bin] += 1
    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(n_bins):
        satisfied_pair += (pos_hist[i]*accumulated_neg + pos_hist[i]*neg_hist[i]*0.5)
        accumulated_neg += neg_hist[i]
    return round(satisfied_pair/float(total_case),2)
N = int(input())
# labels,probs = [],[]
labels , preds = [1,0,1,1,0,1,0,0,1,0] , [0.90,0.70,0.60,0.55,0.52,0.40,0.38,0.35,0.31,0.10]
# for i in range(N):
#     label,pred = map(float,input().split())
#     labels.append(label)
#     preds.append(pred)

res = roc_auc(labels, preds)
print(res)

6. 总结

  • ROC曲线反映了分类器的分类能力，结合考虑了分类器输出概率的准确性
  • AUC量化了ROC曲线的分类能力，越大分类效果越好，输出概率越合理
  • AUC常用作CTR的离线评价，AUC越大，CTR的排序能力越强

7. 大牛的见解

　　［1］From 机器学习和统计里面的auc怎么理解？

　　［2］From 机器学习和统计里面的auc怎么理解？

　　［3］From 精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么？

　　［4］From 多高的AUC才算高？

 参考文献：

【1】如何理解机器学习和统计中的AUC？

 【2】AUC的概率解释

 【3】ROC曲线和AUC面积理解

 【4】ROC曲线-阈值评价标准

 【5】模型评价(一) AUC大法

 【6】ROC曲线与AUC值

posted @ 2019-03-24 00:45  nxf_rabbit75  阅读(3855)  评论(1)  编辑  收藏  举报