22(4).模型融合---Xgboost

一、简介

全称：eXtreme Gradient Boosting

作者：陈天奇

基础：GBDT

所属：boosting迭代型、树类算法

适用范围：回归，分类，排序

xgboost工具包：sklearn xgboost链接 | xgboost工具包(中文)链接 | xgboost工具包(英文)链接

论文链接 | 项目地址 | ppt

优点：

• 显示的把树模型复杂度作为正则项加到优化目标中。
• 公式推导中用到了二阶导数，用了二阶泰勒展开。
• 实现了分裂点寻找近似算法。
• 利用了特征的稀疏性。
• 数据事先排序并且以block形式存储，有利于并行计算。
• 基于分布式通信框架rabit，可以运行在MPI和yarn上。
• 实现做了面向体系结构的优化，针对cache和内存做了性能优化。

缺点：（与LightGBM相比）

• XGBoost采用预排序，在迭代之前，对结点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，LightGBM方法采用histogram算法，占用的内存低，数据分割的复杂度更低；
• XGBoost采用level-wise生成决策树，同时分裂同一层的叶子，从而进行多线程优化，不容易过拟合，但很多叶子节点的分裂增益较低，没必要进行跟进一步的分裂，这就带来了不必要的开销；LightGBM采用深度优化，leaf-wise生长策略，每次从当前叶子中选择增益最大的结点进行分裂，循环迭代，但会生长出更深的决策树，产生过拟合，因此引入了一个阈值进行限制，防止过拟合；

二、Xgboost

1.损失函数

xgboost 也是使用与提升树相同的前向分步算法。其区别在于：xgboost 通过结构风险极小化来确定下一个决策树的参数 ：

最初损失函数：

$L_t=\sum\limits_{i=1}^mL(y_i, f_{t-1}(x_i)+ h_t(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$ 

在GBDT损失函数$L(y, f_{t-1}(x)+ h_t(x))$的基础上，加入正则项$\Omega(h_t) = \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$其中，J是叶子节点的个数，$w_{tj}$是第j个叶子节点的最优值，这里的$w_{tj}$和GBDT中的$c_{tj}$是一个意思，Xgboost论文中用的是w表示叶子的值，这里和论文保持一致。

损失函数的二阶展开：

$\begin{align} L_t & = \sum\limits_{i=1}^mL(y_i, f_{t-1}(x_i)+ h_t(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \\ & \approx \sum\limits_{i=1}^m( L(y_i, f_{t-1}(x_i)) + \frac{\partial L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}(x_i)}h_t(x_i) + \frac{1}{2}\frac{\partial^2 L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}^2(x_i)} h_t^2(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \end{align}$

为了方便，记第i个样本在第t个弱学习器的一阶和二阶导数分别为：

$g_{ti} = \frac{\partial L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}(x_i)}, \; h_{ti} = \frac{\partial^2 L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}^2(x_i)}$

则损失函数可以表达为：

$L_t \approx \sum\limits_{i=1}^m( L(y_i, f_{t-1}(x_i)) + g_{ti}h_t(x_i) + \frac{1}{2} h_{ti} h_t^2(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$

第一项是常数，对最小化loss无影响，可以去掉，同时由于每个决策树的第j个叶子节点的取值最终是同一个值$w_{tj}$，因此损失函数简化为：

$\begin{align} L_t & \approx \sum\limits_{i=1}^m g_{ti}h_t(x_i) + \frac{1}{2} h_{ti} h_t^2(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \\ & = \sum\limits_{j=1}^J (\sum\limits_{x_i \in R_{tj}}g_{ti}w_{tj} + \frac{1}{2} \sum\limits_{x_i \in R_{tj}}h_{ti} w_{tj}^2) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \\ & = \sum\limits_{j=1}^J [(\sum\limits_{x_i \in R_{tj}}g_{ti})w_{tj} + \frac{1}{2}( \sum\limits_{x_i \in R_{tj}}h_{ti}+ \lambda) w_{tj}^2] + \gamma J \end{align}$

把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下：

$G_{tj} = \sum\limits_{x_i \in R_{tj}}g_{ti},\; H_{tj} = \sum\limits_{x_i \in R_{tj}}h_{ti}$

最终损失函数的形式可以表示为：

$L_t = \sum\limits_{j=1}^J [G_{tj}w_{tj} + \frac{1}{2}(H_{tj}+\lambda)w_{tj}^2] + \gamma J$

 

问题1：xgboost如何使用MAE或MAPE作为目标函数？参考链接

xgboost需要目标函数的二阶导数信息（或者hess矩阵），在回归问题中经常将MAE或MAPE作为目标函数，然而，这两个目标函数二阶导数不存在。

$MAE=\frac{1}{n}\sum_1^n|y_i-\hat y_i|$，$MAPE=\frac{1}{n}\sum _i^n \frac{|y_i-\hat y_i|}{y_i}$

其中，$y_i$是真实值，$\hat y_i$是预测值

方法（1）：利用可导的函数逼近MAE或MAPE---MSE、Huber loss、Pseudo-Huber loss

　　利用MSE逼近是可以的，但是MSE在训练初误差较大的时候，loss是其平方，会使得训练偏离MAE的目标函数，一般难以达到高精度的要求。

　　利用Huber loss进行逼近也可以，但是Huber loss是分段函数，不方便计算，其中$\delta$是可调节参数。

　　

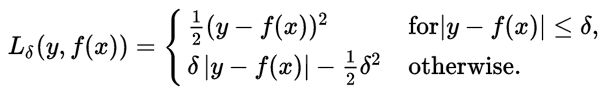
　　实际采用Huber loss的可导逼近形式：Pseudo-Huber loss function

　　

　　一阶导数：

   

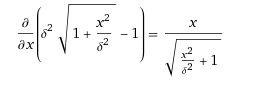
　　二阶导数：

　

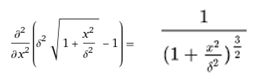
方法（2）：自定义二阶导数的值：$ln(cosh(x))$

 用$ln(cosh(x))$以及$log(exp(-x) + exp(x))$进行逼近

 

$ln(cosh(x))$的一阶导数：$tanh(x)$

$ln(cosh(x))$的二阶导数：$1-tanh(x)*tanh(x)$

2.结构分

当$w_{tj}$取最优解的时候，原损失函数对应的表达式为：$L_t = -\frac{1}{2}\sum\limits_{j=1}^J\frac{G_{tj}^2}{H_{tj} + \lambda} +\gamma J$

在推导过程中假设$w_{tj}$与$T,G_j,H_j$无关，这其实假设已知树的结构。事实上$L_t$是与$T$相关的，甚至与树的结构相关，因此定义$L_t$为结构分。结构分刻画了：当已知树的结构时目标函数的最小值。

3.寻找分裂节点的候选集

Xgboost框架用tree_method[默认为’auto’] 指定了构建树的算法，可以为下列的值(分布式，以及外存版本的算法只支持 ‘approx’,’hist’,’gpu_hist’ 等近似算法)：

+ View Code?

1 2 3 4 5 6 7 8 9

‘auto’： 使用启发式算法来选择一个更快的tree_method： 　　　　　　对于小的和中等的训练集，使用exact greedy 算法分裂节点 　　　　　　对于非常大的训练集，使用近似算法分裂节点 　　　　　　旧版本在单机上总是使用exact greedy 分裂节点 ‘exact’： 使用exact greedy 算法分裂节点 ‘approx’： 使用近似算法分裂节点 ‘hist’： 使用histogram 优化的近似算法分裂节点（比如使用了bin cacheing 优化） ‘gpu_exact’： 基于GPU 的exact greedy 算法分裂节点 ‘gpu_hist’： 基于GPU 的histogram 算法分裂节点

3.1 暴力枚举（exact greedy）

（1）第一种方法是对现有的叶节点加入一个分裂，然后考虑分裂之后目标函数降低多少。

• 如果目标函数下降，则说明可以分裂；
• 如果目标函数不下降，则说明该叶节点不宜分裂。

（2）对于一个叶节点，加入给定其分裂点，定义划分到左子样本节点的集合为：$\mathbb{I_R}$，则有：

（3）定义叶节点的分裂增益为：

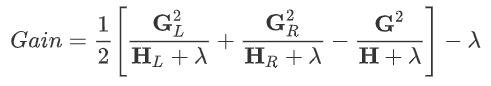
其中，

• $\frac{G^2_L}{H_L+\lambda}$表示：该叶节点的左子树的结构分
• $\frac{G^2_R}{H_R+\lambda}$表示：该叶节点的右子树的结构分
• $\frac{G^2}{H+\lambda}$表示：如果不分裂，则该叶节点自身的结构分
• $-\lambda$表示：因为分裂导致叶节点数量增大1，从而导致增益的下降。

每次只有一个叶节点分裂，因此其他叶节点不会发生变化，因此：

• 若$Gain>0$，则该叶节点应该分裂；
• 若$Gain<0$，则该叶节点不宜分裂。

（4）现在的问题是：不知道分裂点，对于每个叶节点，存在多个分裂点，且可能很多分裂点都能带来增益。

解决办法：对于叶节点中的所有可能的分裂点进行一次扫描。然后计算每个分裂点的增益，选取增益最大的分裂点作为本叶节点的最优分裂点。

（5）最优分裂点贪心算法

输入：$D={(X_1,y_1),(X_2,y_2), ...(X_m,y_m)}$，属于当前叶节点的样本集的下标集合$\mathbb{I}$

输出：当前叶节点最佳分裂点

算法：

　　step1：初始化 $score \leftarrow 0$，$G \leftarrow_{i\in \mathbb{I}}g_i$，$H \leftarrow_{i\in \mathbb{I}}h_i$

　　step2：遍历各维度 $k=1,2,...,m$：

　　　　a)初始化：$G_L \leftarrow 0,H_L \leftarrow 0$

　　　　b)如果第$k$维特征为连续值，则将当前叶节点中的样本从小到大排序。然后用$j$顺序遍历排序后的样本下标。

　　　　

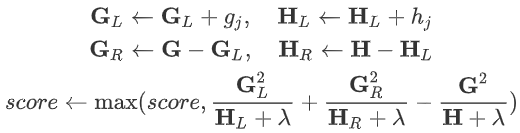
 　　　　c)如果第$k$维特征为离散值${a_1,a_2,...,a_{n_k}}，设当前叶节点中第$k$维取值$a_j$样本的下标集合为$\mathbb{I_j}$，则遍历$j=1,2,...,n_k$：

　　　　

　　step3：选取最大的$score$对应的维度和拆分点作为最优拆分点。

分裂点贪心算法尝试所有特征和所有分裂位置，从而求得最优分裂点。当样本太大且特征为连续值时，这种暴力做法的计算量太大。

3.2 近似算法（approx）

（1）近似算法寻找最优分裂点时不会枚举所有的特征值，而是对特征值进行聚合统计，然后形成若干个桶。然后仅仅将桶边界上的特征的值作为分裂点的候选，从而获取计算性能的提升。

（2）对第k个特征进行分桶，分桶的数量l就是所有样本在第k个特征上的取值的数量。

　　如果第k个特征为连续特征，则执行百分位分桶，得到分桶的区间为：$S_k={s_{k,1},s_{k,2},...,s_{k,l}}$，其中$s_{k,1}<s_{k,2}<...<s_{k,l}$，分桶的数量、分桶的区间都是超参数，需要仔细挑选

　　如果第k个特征为离散特征，则执行按离散值分桶，得到的分桶为：$S_k={s_{k,1},s_{k_2},...,s_{k,l}}$，其中，$s_{k,1}<s_{k,2}<...<s_{k,l}$ 为第k个特征的所有可能的离散值。

（3）最优分裂点近似算法

算法流程：

输入：数据集$D={(X_1,y_1),(X_2,y_2),...,(X_N,y_N)}$，属于当前叶结点的样本集的下标集合$\mathbb{I}$

输出：当前叶节点最佳分裂点

step1：对每个特征进行分桶。假设对第k个特征上的值进行分桶为：$S_k={s_{k,1},s_{k,2},...,s_{k,l}}$，如果第k个特征为连续特征，则要求满足$s_{k,1}<s_{k,2}<...<s_{k,l}$

step2：初始化：$score \leftarrow 0，G\leftarrow \sum_{i\in \mathbb{I}} g_i ,H\leftarrow \sum_{i\in \mathbb{I}} h_i$

step3：遍历各维度：$k=1,...,n$

　　　　初始化：$G_L \leftarrow 0，H_L \leftarrow 0$

　　　　遍历各拆分点，即遍历$j=1,2,...,l$：

　　　　　　如果是连续特征，即设叶节点的样本中，第k个特征取值在区间$(s_{k,j},s_{k,j+1}]$的样本的下标集合为$\mathbb{I}_j$，则：

　　　       　

　　　　　　如果是离散特征，则设叶结点的样本中，第k个特征取值等于$s_{k,j}$的样本的下标集合为$\mathbb{I}$ ，则：

　　         　

　　　　选取最大的score对应的维度和拆分点作为最优拆分点。

（4）分桶有两种模式：

全局模式：在算法开始时，对每个维度分桶一次，后续的分裂都依赖于该分桶并不再更新；

　　优点：只需要计算一次，不需要重复计算；

　　缺点：在经过多次分裂之后，叶节点的样本有可能在很多全局桶中是空的。 

局部模式：每次拆分之后再重新分桶；

　　优点：每次分桶都能保证各桶中的样本数量都是均匀的；

　　缺点：计算量较大。

全局模式会构造更多的候选拆分点，而局部模式会更适合构造构造更深的树。

（5）分桶时的桶区间间隔大小是个重要的参数。区间间隔越小，则桶越多，划分的越精细，候选的拆分点就越多。

3.2.1 Quantile

（1）$\phi$-quantile

Quantile就是ranking。如果有$N$个元素，那么$\phi$-quantile就是指rank在$⌊\phi × N⌋$的元素。例如$S=[11,21,24,61,81,39,89,56,12,51]$，首先排序为$[11,12,21,24,39,51,56,61,81,89]$，则$0.1-quantile=11, 0.5-quantile=39$. 上面的是exact quantile寻找方法，如果数据集非常大，难以排序，则需要引入$\epsilon-approximate \phi-quantiles$

该方法为离线算法（所有的数必须要排序，再找分位点），是不适用于数据流的。

（2）$\epsilon$-approximate $\phi$-quantiles

$\phi$-quantile是在区间$[⌊(\phi−\epsilon)×N⌋,⌊(\phi+\epsilon)×N⌋]$

　　当$N$增加时，$φ$-quantile的“正确”答案（$\epsilon$-近似）的集合增加。因此，您可以从输入流中删除一些元素，并仍保留ε近似分位数查询的正确答案（=询问$\epsilon$近似分位数的查询）

　　回到XGBoost的建树过程，在建立第i棵树的时候已经知道数据集在前面i−1棵树的误差，因此采样的时候是需要考虑误差，对于误差大的特征值采样粒度要加大，误差小的特征值采样粒度可以减小，也就是说采样的样本是需要权重的。

重新审视目标函数：

$$\begin{equation} \sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) \end{equation}$$

通过配方可以得到

$$\begin{equation} \sum_{1}^n \left[ \frac {1}{2} h_i \left( f_t(x_i) - (-g_i/h_i)\right)^2 \right] + \Omega (f_t) + constant \end{equation}$$

因此可以将该目标看做是第$m$棵决策树，关于真实标签为$-\frac{g_i}{h_i}$和权重为$h_i$的、损失函数为平方损失的形式。

3.2.2 Weighted Quantile Sketch

（1）二阶导数$h$为权重的解释

如果损失函数是Square loss，即$Loss(y, \widehat y) = (y - \widehat y)^2$，则$h=2$，那么实际上是不带权；如果损失函数是Log Loss，则$h=pred * (1-pred)$。这是个开口朝下的一元二次函数，所以最大值在0.5。当$pred$在0.5附近，这个值是非常不稳定的，很容易误判，h作为权重则因此变大，那么直方图划分，这部分就会被切分的更细。

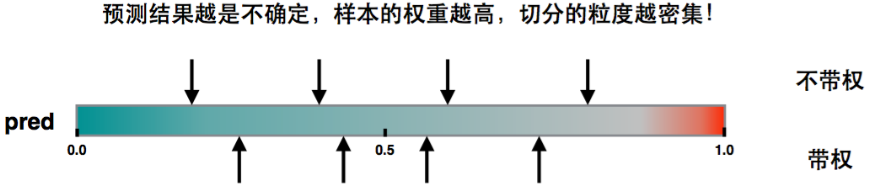
（2）问题转换

　　假设候选样本的第k维特征，及候选样本的损失函数的二阶偏导数为：$\begin{equation} D_k = \{(x_{1k}, h_1), (x_{2k}, h_2), \cdots (x_{nk}, h_n)\} \end{equation}$

　　定义排序函数：$x_{i,k}$表示样本$x_i$的第$k$个特征

　　

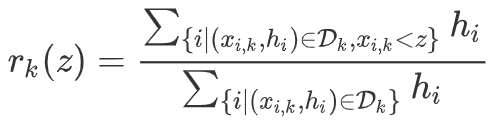
　　它刻画的是：第$k$维特征小于$z$的样本的$h$之和，占总的$h$之和的比例，其中二阶导数$h$可以视为权重，在这个排序函数下，找到一组点$\{ s_{k1}, s_{k2}, ... ,s_{kl} \}$，满足：$\begin{equation} | r_k (s_{k,j}) - r_k (s_{k, j+1}) | < \varepsilon \end{equation}$。

　　其中，${s_{k1}} = \mathop {\min }\limits_i {x_{ik}},{s_{kl}} = \mathop {\max }\limits_i {x_{ik}}$，$\epsilon$为采样率，直观上理解，最后会得到$1/{\epsilon}$个分界点。其中$x_{i,k}$表示样本$x_i$的第$k$个特征，即：

　　最小的拆分点：所有样本第$k$维的最小值；

　　最大的拆分点：所有样本第$k$维的最大值；

　　中间的拆分点：选取拆分点，使得相邻拆分点的排序函数值小于$\epsilon$（分桶的桶宽）。其意义为：第$k$维大于等于$s_{k,j}$，小于$s_{k,j+1}$的样本的$h$之和，占总的$h$之和的比例小于$\epsilon$；这种拆分点使得每个桶内的以$h$为权重的样本数量比较均匀，而不是样本个数比较均匀。

举例：

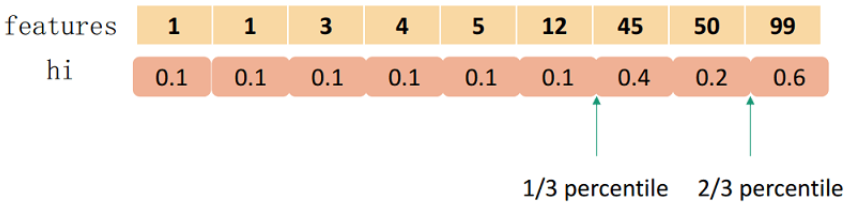
 要切分为3个，总和为1.8，因此第1个在0.6处，第2个在1.2处。

　　对于每个样本都有相同权重的问题，有quantile sketch算法解决该问题，作者提出Weighted Quantile Sketch算法解决这种weighted datasets的情况

（3）Weighted Quantile Sketch算法

问题：To design an algorithm, you must first design an adequate data structure to maintain the information used by the algorithm

a) [$v_i，min_i，max_i$]

 

 

 

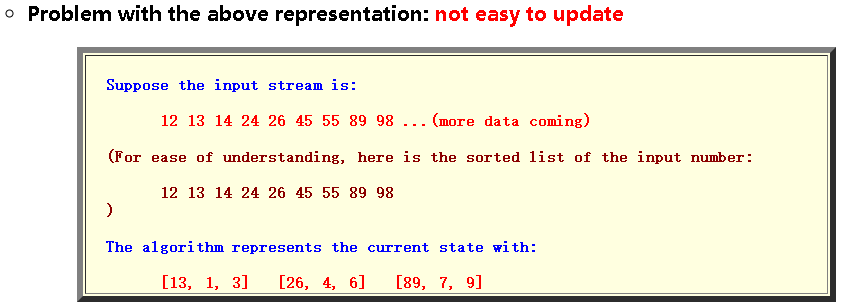
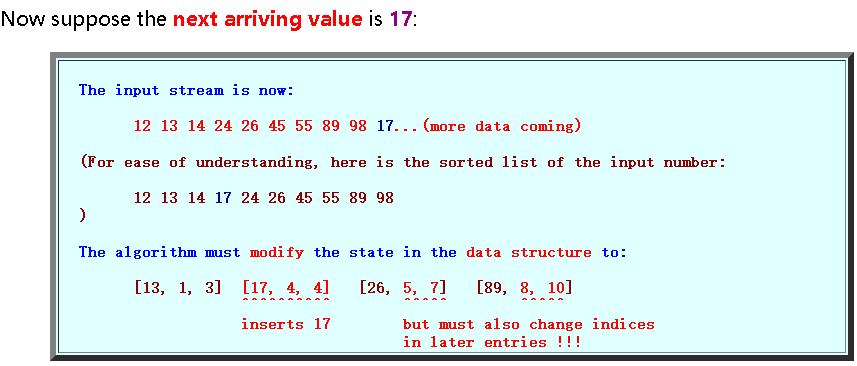
该数据结构需要每插入值进行大量操作。 虽然它很有用，但效率不高

b) [$v_i，g_i$]

 

 这个数据结构存在问题：它不包含足够的信息来删除不必要的条目 

c) Greenwald & Khanna's 算法：[$v_i,g_i,\triangle_i$]

 定义：

 

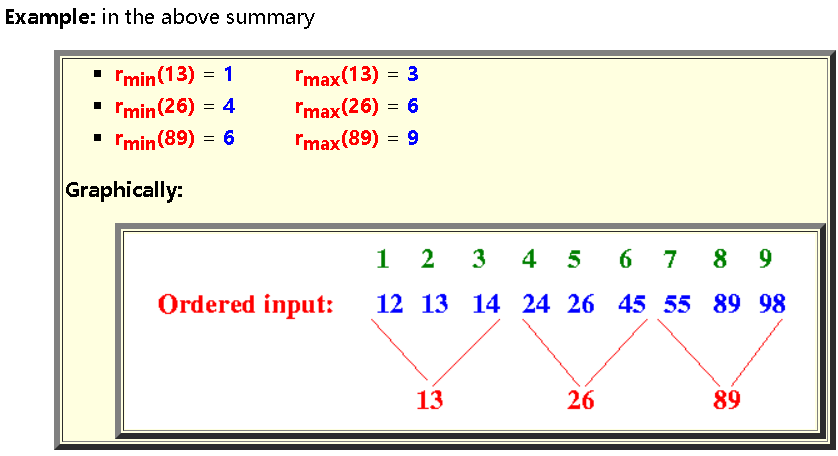
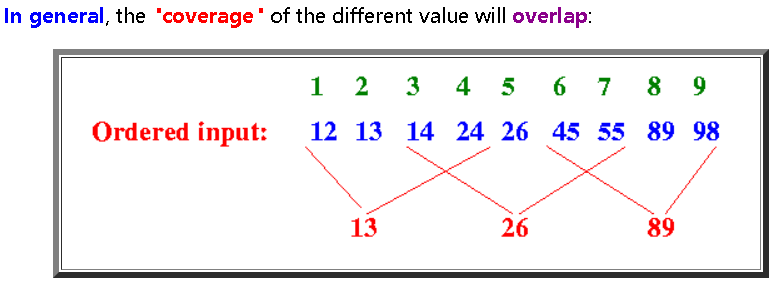
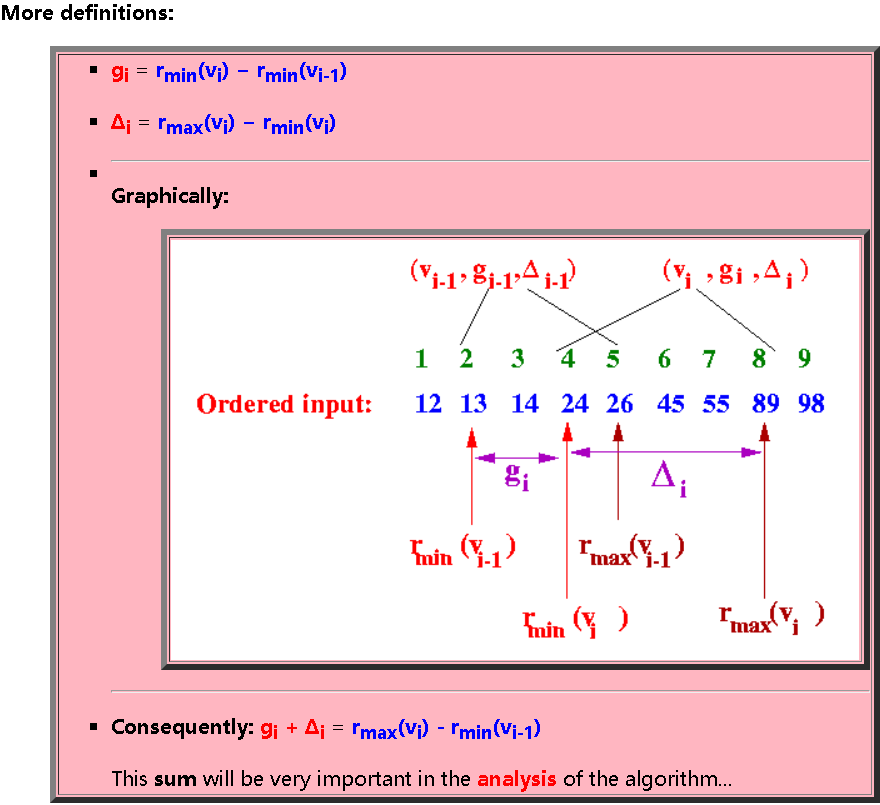
$v_0$=目前为止遇到的最小的数

$v_{s-1}$=目前为止遇到的最大的数

三个性质：

• 性质1：$r_{min}(v_i) = \sum_{j=0}^{i}g_j$

• 性质2：$r_{max}(v_i) = \sum_{j=0}^{i}g_j+\triangle_i$

• 性质3：$g_0+g_1+...+g_{s-1}=N$

举例：

命题1：summary达到的准确度，误差$e=max_{all i}(g_i+\triangle_i)/2$

推论1：Greenwald和Khanna算法的不变性

GK算法框架：先判断是否要合并，再插入

 插入算法：

• Inserting an arriving value must maintain the consistency of the information in the summary

证明

删除算法：

 how to use the quantile summary？

• The quantile summary is used to answer quantile queries 
• Given a ε-approximate quantile summary, how do we use it to answer a quantile queries ?

 

3.3 直方图算法（hist）

直方图聚合是树木生长中的主要计算瓶颈。我们引入了一种新的树生长方法hist，其中只考虑了可能的分裂值的子集。与FastBDT和LightGBM一样，连续特征被分成不连续的区域。由于较少的索引操作，直方图累积变得更快

新方法与tree_method = approx有何不同？

• xgboost中现有的近似分裂方法还将连续特征存储到离散区间以加速训练。 approx方法为每次迭代生成一组新的bin，而hist方法在多次迭代中重用bin。

hist方法可以实现approx方法无法实现的额外优化，如下所示：

• 箱的缓存：用bin ID替换训练数据中的连续特征值并缓存数据结构
• 直方图减法技巧：为了计算一个节点的直方图，我们简单地取其父和兄弟的直方图之间的差异。

除了上述改进之外，还有一些亮点

• 自然支持稀疏矩阵的有效表示，如xgboost，稀疏矩阵，混合稀疏+密集矩阵的有效加速
• 可扩展到xgboost中的其他现有功能，例如单调约束，语言绑定。

如何使用？

• 只需将tree_method设置为hist即可。您可能还需要设置max_bin，它表示存储连续特征的（最大）离散区间数。默认情况下，max_bin设置为256.增加此数字可以提高分割的最佳性，但代价是计算时间较长。

 

 

4.缺失值

（1）真实场景中，有很多可能导致产生稀疏。如：数据缺失、某个特征上出现很多 0 项、人工进行 one-hot 编码导致的大量的 0。

• 理论上，数据缺失和数值0的含义是不同的，数值 0 是有效的。
• 实际上，数值0的处理方式类似缺失值的处理方式，都视为稀疏特征。
• 在xgboost 中，数值0的处理方式和缺失值的处理方式是统一的。这只是一个计算上的优化，用于加速对稀疏特征的处理速度。
• 对于稀疏特征，只需要对有效值进行处理，无效值则采用默认的分裂方向。

　　注意：每个结点的默认分裂方向可能不同。

（2）在xgboost 算法的实现中，允许对数值0进行不同的处理。可以将数值0视作缺失值，也可以将其视作有效值。 如果数值0是有真实意义的，则建议将其视作有效值。

（3）缺失值处理算法

输入：数据集$D={(X_1,y_1),(X_2,y_2),...,(X_N,y_N)}$

　　　属于当前叶结点的样本集的下标集合$\mathbb{I}$

　　　属于当前叶节点，且第$k$维特征有效的样本的下标集合$\mathbb{I}_k = \{{i\in \mathbb{I}| x_{k,i}\neq missing}\}$

输出：当前叶节点最佳分裂点

step1：初始化：$score \leftarrow 0，G\leftarrow \sum_{i\in \mathbb{I}} g_i ,H\leftarrow \sum_{i\in \mathbb{I}} h_i$

step3：遍历各维度：$k=1,...,n$

　　　   先从左边开始遍历：

　　　　　　初始化：$G_L \leftarrow 0，H_L \leftarrow 0$

　　　　　　遍历各拆分点：沿着第$k$维，将当前有效的叶节点的样本从小到大排序。这相当于所有无效特征值的样本放在最右侧，因此可以保证无效的特征值都在右子树。然后用$j$顺序遍历排序后的样本下标：

　　　　　　

 

 　　　　再从右边开始遍历：

　　　　　　初始化：$G_R \leftarrow 0，H_R \leftarrow 0$

　　　　　　遍历各拆分点：沿着第$k$维，将当前有效的叶节点的样本从大到小排序。这相当于所有无效特征值的样本放在最左侧，因此可以保证无效的特征值都在左子树。然后用$j$逆序遍历排序后的样本下标：

　　　　　　

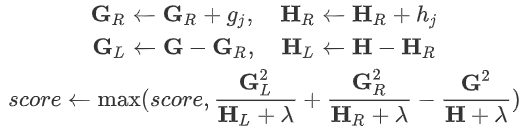
　　　　选取最大的score对应的维度和拆分点作为最优拆分点。

缺失值处理算法中，通过两轮遍历可以确保稀疏值位于左子树和右子树的情形。

5. 其他优化

5.1 正则化

xgboost在学习过程中使用了如下的正则化策略来缓解过拟合：

• 通过学习率$v$来更新模型：$f_m(x)=f_{m-1}(x)+vh_m(x;\theta_m)$，$0<v<=1$，也叫shrinkage
• 类似于随机森林，采取随机属性选择，也叫col_sample

5.2 计算速度提升

xgboost在以下方面提出改进来提升计算速度：

• 预排序pre-sorted；
• cache-aware预取；
• Out-of-Core大数据集

5.2.1 预排序

（1）xgboost提出column block数据结构来降低排序时间。

• 每一个block代表一个特征的值，样本在该block中按照它在该特征的值排好序。这些block只需要在程序开始的时候计算一次，后续排序只需要线性扫描这些block即可。
• Block中的数据以稀疏格式CSC进行存储。
• 由于属性之间是独立的，因此在每个维度寻找划分点可以并行计算。

时间复杂度减少：

• 在Exact greedy算法中，将整个数据集存放在一个Block中。这样，复杂度从原来的$O(Hd||x||_0logn)$降为$O(Hd||x||_0+||x||_0logn)$，其中$||x||_0$为训练集中非缺失值的个数。这样，Exact greedy算法就省去了每一步中的排序开销。 在近似算法中，使用多个Block，每个Block对应原来数据的子集。不同的Block可以在不同的机器上计算。该方法对Local策略尤其有效，因为Local策略每次分支都重新生成候选切分点。

（2）block可以仅存放样本的索引，而不是样本本身，这样节省了大量的存储空间。

如：block_1代表所有样本在feature_1上的从小到大排序：sample_no1,sample_no2,...

其中样本编号出现的位置代表了该样本的排序。

可以看出，只需在建树前排序依次，后面节点分裂时可以直接根据索引得到梯度信息。

5.2.2 预取

（1）由于在column block中，样本的顺序会被打乱，这会使得从导数数组中获取$g_i$时的缓存命中率较低。

因此，xgboost提出了cache-aware预取算法，对每个线程分配一个连续的buffer，读取梯度信息并存入Buffer中（这样就实现了非连续到连续的转化），然后再统计梯度信息。该方式在训练样本数大的时候特别有用，用于提升缓存命中率。

（2）xgboost会以minibatch的方式累加数据，然后在后台开启一个线程来加载需要用到的导数$g_i$。

这里有个折中：minibatch太大，会引起cache miss；太小，则并行程度较低。

5.2.3 Out-of-Core

（1）xgboost利用硬盘来处理超过内存容量的大数据量，其中使用了下列技术：

• 使用block压缩技术来缓解内存和硬盘的数据交换IO：数据按列压缩，并且在硬盘到内存的传输过程中被自动解压缩；
• 数据随机分片到多个硬盘，每个硬盘对应一个预取线程，从而加大“内存-硬盘”交换数据的吞吐量。

 

 

 

参考文献：

【1】XGBoost算法原理小结

【2】xgboost如何使用MAE或MAPE作为目标函数?

【3】XGBoost解读(2)--近似分割算法

【4】ε-approximate quantiles

【5】『我爱机器学习』集成学习（三）XGBoost - 细语呢喃

【6】gbdt.pdf

【7】Xgboost系统设计：分块并行、缓存优化和Blocks for Out-of-core Computation - anshuai_aw1的博客 - CSDN博客