22(3).模型融合---Adaboost
一、简介
Boosting 是一类算法的总称,这类算法的特点是通过训练若干弱分类器,然后将弱分类器组合成强分类器进行分类。为什么要这样做呢?因为弱分类器训练起来很容易,将弱分类器集成起来,往往可以得到很好的效果。俗话说,"三个臭皮匠,顶个诸葛亮",就是这个道理。这类 boosting 算法的特点是各个弱分类器之间是串行训练的,当前弱分类器的训练依赖于上一轮弱分类器的训练结果。各个弱分类器的权重是不同的,效果好的弱分类器的权重大,效果差的弱分类器的权重小。值得注意的是,AdaBoost 不止适用于分类模型,也可以用来训练回归模型。这需要将弱分类器替换成回归模型,并改动损失函数。
进入正题之前,先来看Adaboost的两个核心问题:
- 在每一轮学习之前,如何改变训练数据的权值分布?
- 如何将一组弱分类器组合成一个强分类器?
针对第一个问题,Adaboost算法的做法是:
提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。如此,那些没有得到正确分类的样本,由于其权值加大而受到后一轮的弱分类器的更大关注。
第二个问题,弱分类器的组合,AdaBoost采取加权多数表决的方法。具体地:
加大 分类误差率小 的弱分类器的权值,使其在表决中起较大的作用;减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
AdaBoost算法的巧妙之处就在于它将这些学习思路自然并且有效地在一个算法里面实现。
几个误区:
- Adaboost算法基本原理就是将多个弱分类器(弱分类器一般选用单层决策树)进行合理的结合,使其成为一个强分类器。
- 弱学习器:在二分情况下弱分类器的错误率会低于50%。其实任意的分类器都可以做为弱分类器,比如之前介绍的KNN、决策树、Naive Bayes、logiostic回归和SVM都可以。
1. Adaboost 的算法的流程?
重点关注以下4个问题
- 如何计算学习误差率e?
- 如何得到弱学习器权重系数α?
- 如何更新样本权重D?
- 使用何种结合策略?
本节主要介绍Adaptive Boosting。首先通过讲一个老师教小学生识别苹果的例子,来引入Boosting的思想,即把许多“弱弱”的hypotheses合并起来,变成很强的预测模型。然后重点介绍这种算法如何实现,关键在于每次迭代时,给予样本不同的系数u,宗旨是放大错误样本,缩小正确样本,得到不同的小矩g。并且在每次迭代时根据错误ϵ值的大小,给予不同gt不同的权重。最终由不同的gt进行组合得到整体的预测模型G。实际证明,Adaptive Boosting能够得到有效的预测模型。
(1)引入
我们先来看一个简单的识别苹果的例子,老师展示20张图片,让6岁孩子们通过观察,判断其中哪些图片的内容是苹果。从判断的过程中推导如何解决二元分类问题的方法。
显然这是一个监督式学习,20张图片包括它的标签都是已知的。首先,学生Michael回答说:所有的苹果应该是圆形的。根据Michael的判断,对应到20张图片中去,大部分苹果能被识别出来,但也有错误。其中错误包括有的苹果不是圆形,而且圆形的水果也不一定是苹果。如下图所示:

上图中蓝色区域的图片代表分类错误。显然,只用“苹果是圆形的”这一个条件不能保证分类效果很好。我们把蓝色区域(分类错误的图片)放大,分类正确的图片缩小,这样在接下来的分类中就会更加注重这些错误样本。
然后,学生Tina观察被放大的错误样本和上一轮被缩小的正确样本,回答说:苹果应该是红色的。根据Tina的判断,得到的结果如下图所示:

上图中蓝色区域的图片一样代表分类错误,即根据这个苹果是红色的条件,使得青苹果和草莓、西红柿都出现了判断错误。那么结果就是把这些分类错误的样本放大化,其它正确的样本缩小化。同样,这样在接下来的分类中就会更加注重这些错误样本。
接着,学生Joey经过观察又说:苹果也可能是绿色的。根据Joey的判断,得到的结果如下图所示:
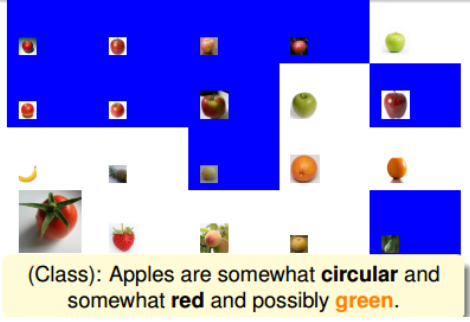
上图中蓝色区域的图片一样代表分类错误,根据苹果是绿色的条件,使得图中蓝色区域都出现了判断错误。同样把这些分类错误的样本放大化,其它正确的样本缩小化,在下一轮判断继续对其修正。
后来,学生Jessica又发现:上面有梗的才是苹果。得到如下结果:


(2)Diversity by Re-weighting



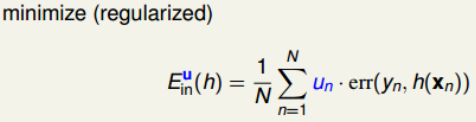 其实,这种weightd base algorithm我们之前就见过类似的算法形式。例如在soft-margin SVM中,我们引入允许犯错的项,同样可以将每个点的error乘以权重因子un 。加上该项前的参数C,经过QP,最终得到0≤αn≤Cun,有别于之前介绍的0≤α≤C。这里的un 相当于每个犯错的样本的惩罚因子,并会反映到αn 的范围限定上。
其实,这种weightd base algorithm我们之前就见过类似的算法形式。例如在soft-margin SVM中,我们引入允许犯错的项,同样可以将每个点的error乘以权重因子un 。加上该项前的参数C,经过QP,最终得到0≤αn≤Cun,有别于之前介绍的0≤α≤C。这里的un 相当于每个犯错的样本的惩罚因子,并会反映到αn 的范围限定上。


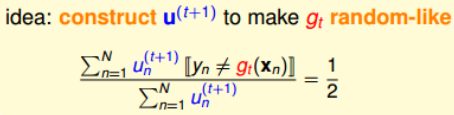
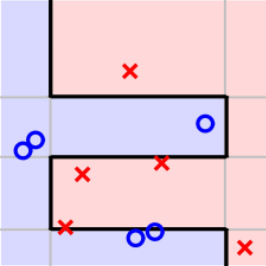
乍看上面这个式子,似乎不好求解。但是,我们对它做一些等价处理,其中分式中分子可以看成gt作用下犯错误的点,而分母可以看成犯错的点和没有犯错误的点的集合,即所有样本点。其中犯错误的点和没有犯错误的点分别用橘色方块和绿色圆圈表示:



(3)Adaptive Boosting Algorithm






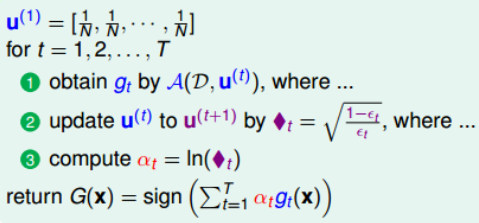


综上所述,完整的adaptive boosting(AdaBoost)Algorithm流程如下:

从我们之前介绍过的VC bound角度来看,AdaBoost算法理论上满足:



(4)举例:
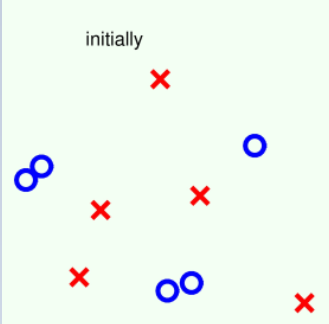
【例1】
初始:
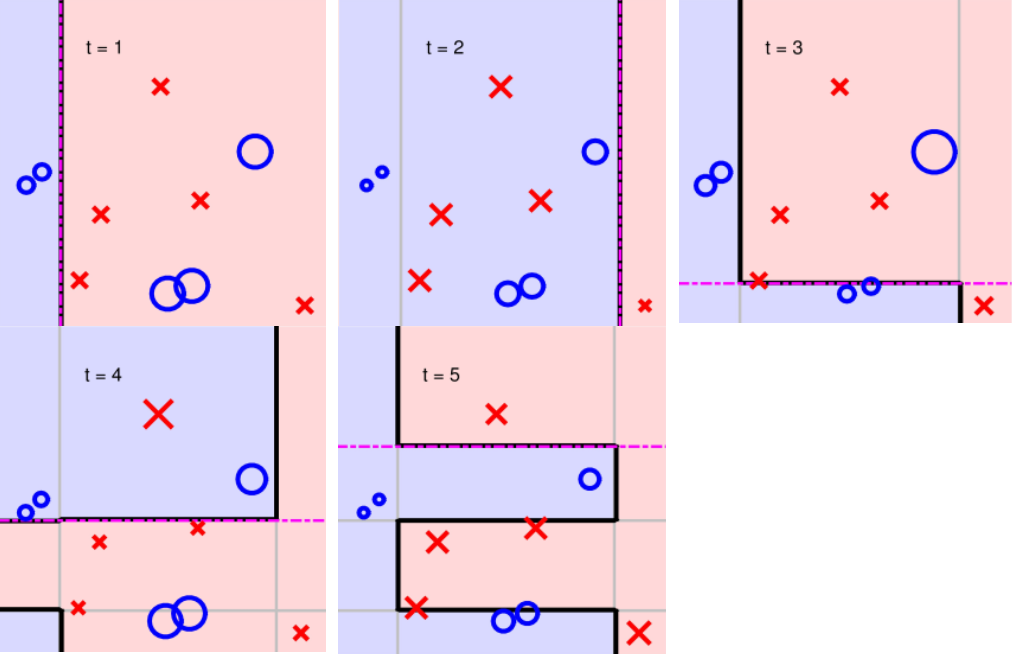
迭代五次:
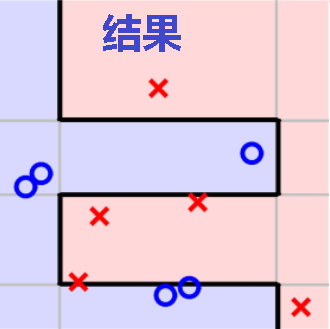


【例3】




2.Adaboost 如何用于分类?


3.Adaboost 如何用于回归?


【拓展】为什么每个样本最终的结果取分类器得到所有值排序之后的中位数作为最终的结果?
答:因为中位数的值能够使得误差最小,具体证明见下图

4.Adaboost 的参数有哪些,如何调参 ?
(1)框架参数
base_estimator:A理论上可以选择任何一个分类或者回归学习器,不过需要支持样本权重。我们常用的一般是CART决策树或者神经网络MLP。默认是决策树.另外有一个要注意的点是,如果我们选择的AdaBoostClassifier算法是SAMME.R,则我们的弱分类学习器还需要支持概率预测,也就是在scikit-learn中弱分类学习器对应的预测方法除了predict还需要有predict_proba。
algorithm:这个参数只有AdaBoostClassifier有。主要原因是scikit-learn实现了两种Adaboost分类算法,SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量,SAMME使用了和我们的原理篇里二元分类Adaboost算法的扩展,即用对样本集分类效果作为弱学习器权重,而SAMME.R使用了对样本集分类的预测概率大小来作为弱学习器权重。由于SAMME.R使用了概率度量的连续值,迭代一般比SAMME快,因此AdaBoostClassifier的默认算法algorithm的值也是SAMME.R。我们一般使用默认的SAMME.R就够了,但是要注意的是使用了SAMME.R, 则弱分类学习器参数base_estimator必须限制使用支持概率预测的分类器。SAMME算法则没有这个限制。
loss:这个参数只有AdaBoostRegressor有,Adaboost.R2算法需要用到。有线性‘linear’, 平方‘square’和指数 ‘exponential’三种选择, 默认是线性,一般使用线性就足够了,除非你怀疑这个参数导致拟合程度不好。
n_estimators:太小容易欠拟合,太大容易过拟合,默认50
learning_rate:fk(x)=fk−1(x)+ναkGk(x),v就是学习率,较小的v意味着需要更多的弱学习器的迭代次数。通常我们用步长和迭代次数一起来决定算法的拟合效果,可以从一个小一点的v开始调参,默认是1.
(2)弱学习器参数
max_features:划分时考虑的最大特征数。默认是“None”,可以使用很多种类型的值,默认是"None",意味着划分时考虑所有的特征数;如果是"log2"意味着划分时最多考虑log2N个特征;如果是"sqrt"或者"auto"意味着划分时最多考虑N−−√个特征。如果是整数,代表考虑的特征绝对数。如果是浮点数,代表考虑特征百分比,即考虑(百分比xN)取整后的特征数。其中N为样本总特征数。一般来说,如果样本特征数不多,比如小于50,我们用默认的"None"就可以了,如果特征数非常多,我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数,以控制决策树的生成时间。
max_depth:默认可以不输入,如果不输入的话,决策树在建立子树的时候不会限制子树的深度。一般来说,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间。
min_samples_split:内部节点再划分所需最小样本数。这个值限制了子树继续划分的条件,如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
min_samples_leaf:叶子节点最少样本数。 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数,或者最少样本数占样本总数的百分比。如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
min_weight_fraction_leaf:叶子节点最小的样本权重和。这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝。 默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。
max_leaf_nodes:通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制,具体的值可以通过交叉验证得到。
5.Adaboost 的优缺点 ?
- Adaboost作为分类器时,分类精度很高
- 在Adaboost的框架下,可以使用各种回归分类模型来构建弱学习器,非常灵活。
- 作为简单的二元分类器时,构造简单,结果可理解。
- 不容易发生过拟合
- 在Adaboost训练过程中,Adaboost会使得难于分类样本的权值呈指数增长,训练将会过于偏向这类困难的样本,导致Adaboost算法易受噪声干扰。此外,Adaboost依赖于弱分类器,而弱分类器的训练时间往往很长。
参考文献:
【2】AdaBoost原理详解



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现