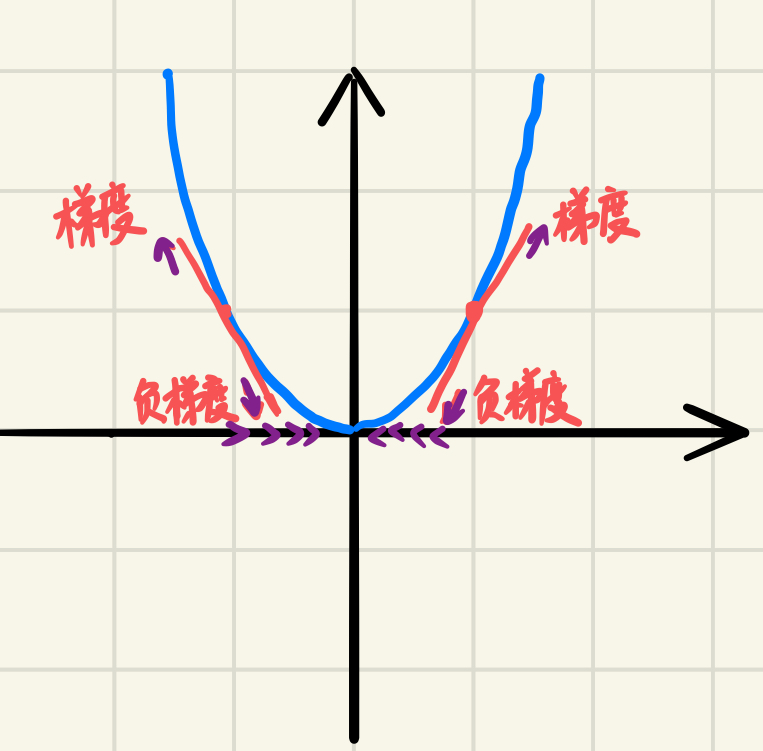
梯度的方向
梯度:如果函数是一维的变量,则梯度就是导数的方向;如果是大于一维的,梯度就是在这个点的法向量,并指向数值更高的等值线。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)
梯度上升:如果我们需要求解损失函数的最大值,用梯度上升法来迭代求解。
梯度下降:在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解,但当目标函数是凸函数时,梯度下降法的解是全局解。θi=θi−α∂∂θiJ(θ0,θ1...,θn)
- 假设函数(hypothesis function):例如线性回归的拟合函数为hθ(x)=θ0+θ1x
- 损失函数:J(θ0,θ1...,θn)=12mm∑j=0(hθ(x(j)0,x(j)1,...x(j)n)−yj)2
- 算法调优:
- 步长(learning rate):步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度
- 参数的初始值选择:由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
- 连续特征归一化
梯度下降法公式的推导:
一阶泰勒:f(x+Δx)=f(x)+f′(x)∗Δx
目的是使得左边的值最小,那应该使得f′(x)Δx为负数,
令Δx=−f′(x),这样上式就变为f(x+Δx)=f(x)−f′(x)∗f′(x)
但是上式只在局部成立,加上修正因子,就变为Δx=−λ∗f′(x),
最终得到:xn+1=xn−λ∗f′(xn)
最速下降法过程:
输入:目标函数f(x),梯度函数g(x)=Δf(x),计算精度ϵ
输出:f(x)的极小点x∗
- step 1:取初始值x(0)属于Rn,置k=0
- step 2:计算f(x(k))
- step 3:计算梯度gk=g(x(k)),当||gk||<ϵ时,停止迭代,令x∗=x(k);否则,令pk=−g(x(k)),求λk,使f(x(k)+λkpk)=minf(x(k)+λpk),λ≥0
- step 4:置x(k+1)=x(k)+λkpk,计算f(x(k+1)),当||f(x(k+1))−f(x(k))||<ϵ或||x(k+1)−x(k)||<ϵ,停止迭代,令x∗=x(k+1)
- step 5:否则,置k=k+1,转step 3
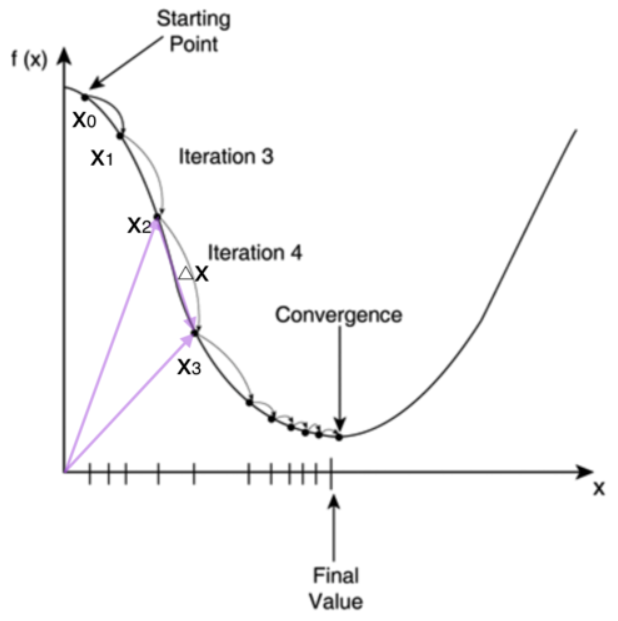
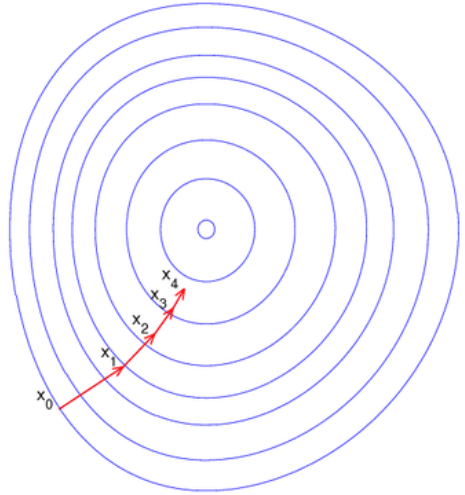
梯度下降 梯度下降方向俯视图
沿着梯度的方向为什么是函数值增加最快的方向?
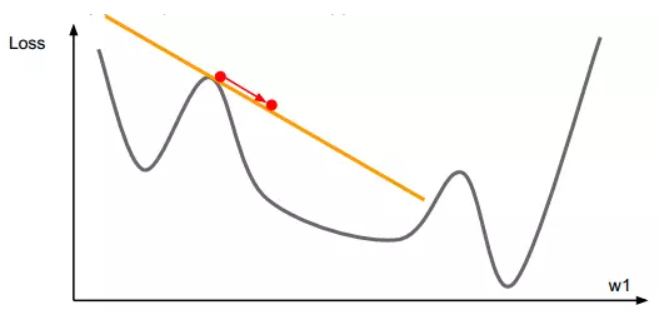
梯度下降一阶优化
一、梯度下降家族
1.1 批量梯度下降法(Batch Gradient Descent,BGD)
θi=θi−αm∑j=0(hθ(x(j)0,x(j)1,...x(j)n)−yj)x(j)i
m个样本都用来更新参数
时间复杂度:O(mnT)
1.2 随机梯度下降法(Stochastic Gradient Descent,SGD)
θi=θi−α(hθ(x(j)0,x(j)1,...x(j)n)−yj)x(j)i
SGD每次更新参数时,仅使用一个样本j。
时间复杂度:O(nT)
1.3 小批量梯度下降法(Mini-batch Gradient Descent,MBGD)
θi=θi−αt+x−1∑j=t(hθ(x(j)0,x(j)1,...x(j)n)−yj)x(j)i
BGD和SGD的折中,对于m个样本,采用x个子样本来更新参数,1<x<m
时间复杂度:O(xnT)
特点:
- 速度快
- 收敛慢
- 容易跳出鞍点:因为每次迭代使用一个样本,使用的梯度不是很准确,就降低了陷入局部极小与鞍点的几率。
二、牛顿家族
2.1 牛顿法
(1)用牛顿法求f(x)=0的根
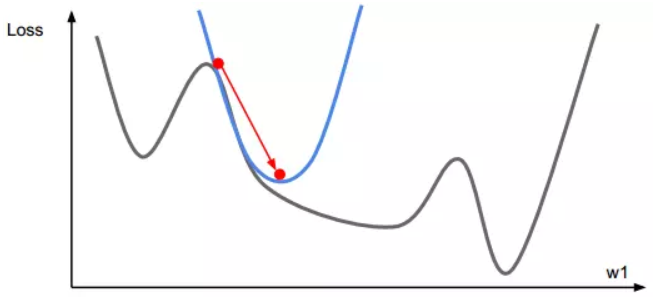
牛顿法二阶优化
先随机选个初始点x0,然后开始迭代,
xn+1=xn−f(xn)f′(xn)
当|xn+1−xn|<ϵ,迭代结束,xn+1就是f(x)=0的近似值解。此处牛顿法是一阶算法。
举例:用牛顿法近似求解根号2
def func(x):
return x ** 2 - 2
def f_func(x):
return 2 * x
x = 1.5
err = f_func(x)
while abs(func(x)) > 0.000001:
x = x - func(x) / f_func(x)
print(x)
|
(2)用牛顿法用作优化算法时候,它是二阶的
假设有一个凸优化问题minxf(x),问题是找一个x来最小化f(x)
牛顿法公式的推导:
二阶泰勒:f(x+Δx)=f(x)+f′(x)Δx+1/2∗f′′(x)∗Δx2
希望左式最小,将左式看作Δx的函数,当取合适的Δx值时,左边式子达到极小值,此时导数为0,得到0=f′(x)+f′′(x)∗Δx
利用牛顿法求解,选取初始点x0,然后进行如下迭代:
xn+1=xn−f′(xn)f′′(xn)
直到|xn+1−xn|<ϵ
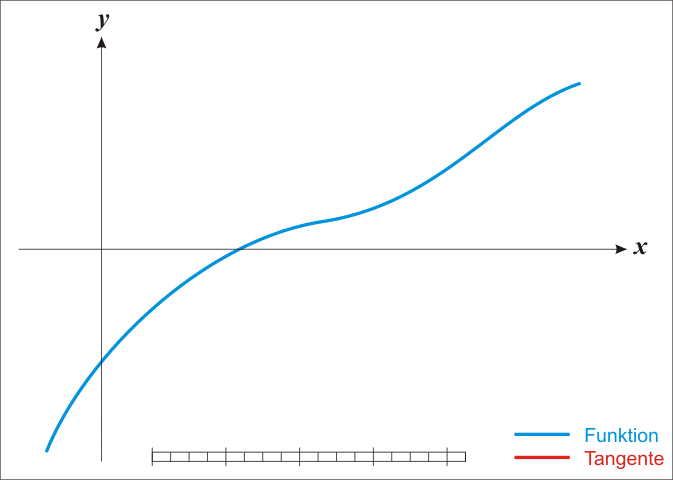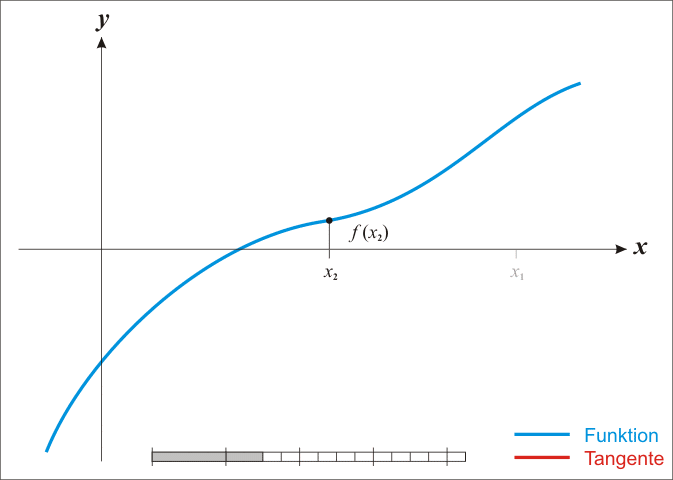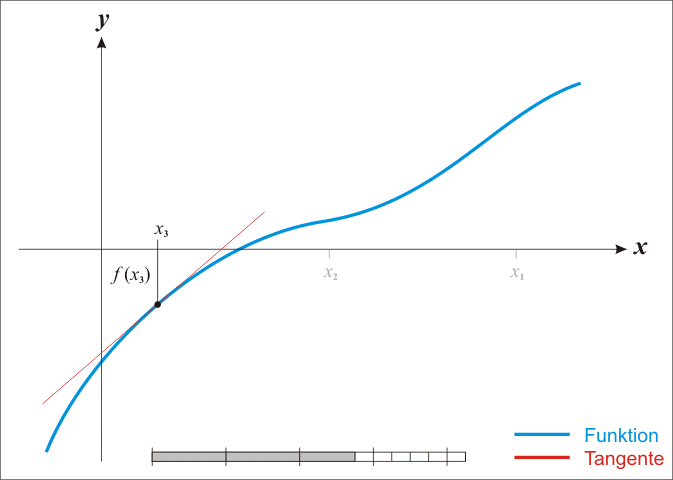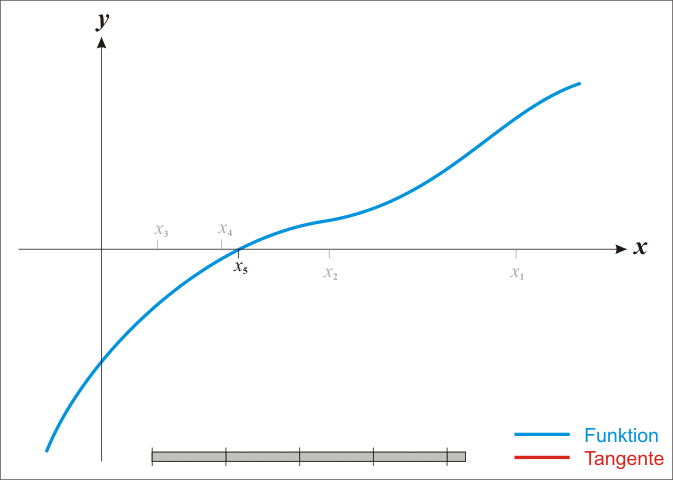
牛顿法过程:
输入:目标函数f(x),梯度g(x)=Δf(x),海瑟矩阵H(x),精度要求ϵ
输出:f(x)的极小点
- step 1:取初始点x(0),置k=0
- step 2:计算gk=g(x(k))
- step 3:若||gk||≤ϵ,则停止计算,得近似解x∗=x(k)
- step 4:计算Hk=H(x(k)),并求pk,Hkpk=−gk(pk=−H−1kgk计算海瑟矩阵比较复杂)
- step 5:置x(k+1)=x(k)+pk
- step 6:置k=k+1,转step 2
优点:
- 二阶收敛,收敛速度快;
- 如果G∗正定,且初始点合适,算法二阶收敛、对正定二次函数,迭代一次就可以得到极小点
缺点:
- 牛顿法是一种迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
- 牛顿法需要Hessian矩阵正定,如果非正定,会陷入鞍点
- 当初始点远离极小点时,牛顿法可能不受理,原因可能是因为牛顿方向不一定是下降方向,经迭代,目标函数值可能上式,此外,即使目标函数值下降,得到的点x(k+1)也不一定是沿牛顿方向的最好点或极小点。
2.2 阻尼牛顿法
牛顿法最突出的优点是收敛速度快,具有局部二阶收敛性,但是,基本牛顿法初始点需要足够“靠近”极小点,否则,有可能导致算法不收敛。这样就引入了阻尼牛顿法,阻尼牛顿法最核心的一点在于可以修改每次迭代的步长,通过沿着牛顿法确定的方向一维搜索最优的步长,最终选择使得函数值最小的步长。
阻尼牛顿法与牛顿法区别在于增加了沿牛顿方向的一维搜索,迭代公式为x(k+1)=x(k)+λkd(k),其中,d(k)=−Δ2f(x(k))−1Δ2f(x(k))为牛顿方向,λk是一维搜索得到的步长,满足f(x(k)+λkd(k))=minλf(x(k)+λd(k))
计算过程:
- step 1:取初始点x(1),允许误差ϵ>0,置k=1
- step 2:计算Δf(x(k)),Δ2f(x(k))−1
- step 3:若||Δf(x(k))||<ϵ,则停止计算,否则,令d(k)=−Δ2f(x(k))−1Δf(x(k))
- step 4:从x(k)出发,沿方向d(k)作一维搜索,f(x(k)+λkd(k))=minf(x(k)+λd(k)),令x(k+1)=x(k)+λkd(k)
- step 5:置k=k+1,转step 2
三、拟牛顿家族
前面介绍了牛顿法,它的突出优点是收敛很快,但是运用牛顿法需要计算二阶偏导数,而且目标函数的Hesse矩阵可能非正定。为了克服牛顿法的缺点,人们提出了拟牛顿法,它的基本思想是用不包含二阶导数的矩阵近似牛顿法中的Hesse矩阵的逆矩阵。 由于构造近似矩阵的方法不同,因而出现不同的拟牛顿法。
拟牛顿法公式推导:
设在第k次迭代后,得到点x(k+1),将目标函数f(x)在点x(k+1)展开成二阶泰勒级数f(x)≈f(x(k+1))+Δf(x(k+1))T(x−x(k+1))+12(x−x(k+1))TΔ2f(x(k+1)))(x−x(k+1))
令x=x(k),则f(x(k))≈f(x(k+1))+Δf(x(k+1))T(x−x(k+1))+12(x−x(k+1))TΔ2f(x(k+1)))(x(k)−x(k+1))
记p(k)=x(k+1)−x(k),q(k)=Δf(x(k+1))−Δf(x(k))则q(k)≈Δ2f(x(k+1))p(k)
又设Hesse矩阵Δ2f(x(k+1))可逆,则p(k)≈Δ2f(x(k+1))−1q(k)
计算出p(k)和q(k)后,可以根据上式估计在x(k+1)处的Hesse矩阵的逆,所以拟牛顿的条件就是p(k)=Hk+1q(k)
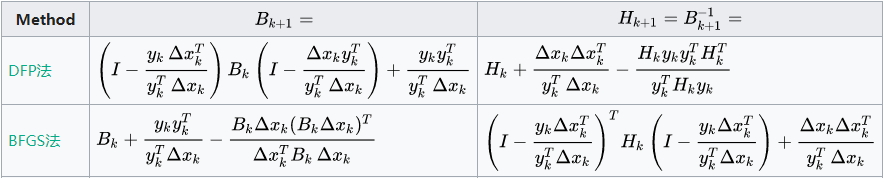
wiki关于拟牛顿法的公式
| Method |
Bk+1 |
Hk+1 |
| DFP |
|
Hk+1=Hk+p(k)p(k)Tp(k)Tq(k)−Hkq(k)q(k)THkq(k)THkq(k) |
| BFGS |
Bk+1=Bk+q(k)q(k)Tq(k)Tp(k)−Bkp(k)p(k)TBkp(k)TBkp(k) |
|
3.1 DFP
用不包含二阶导数的矩阵Hk近似代替牛顿法中的Hesse矩阵的逆矩阵G−1k。
秩1校正推导过程:当G为n阶对称正定矩阵时,满足拟牛顿条件的矩阵Hk也应该是n阶对称正定矩阵,构造策略为,H1取为任意一个n阶对称正定矩阵,通常选择为n阶单位矩阵I,然后通过修正Hk给出Hk+1,
令Hk+1=Hk+ΔHk,(1)
其中,ΔHk称为校正矩阵。
令ΔHk=αkz(k)(z(k)T),(2)
αk是一个常数,z(k)是n维列向量,这样定义的ΔHk是秩为1的对称矩阵,
令p(k)=Hkq(k)+αkz(k)z(k)Tq(k),(3)
由此得到z(k)=p(k)−Hkq(k)αkz(k)Tq(k),(4)
另一方面,(3)式等号两端左乘以q(k)T,整理得到
q(k)T(p(k)−Hkq(k))=αk(z(k)Tq(k))2,(5)
利用 (2)(4)(5),把(1)式写成:
Hk+1=Hk+p(k)−Hkq(k)p(k)−Hkq(k)Tq(k)T(p(k)−Hkq(k))
后来,Davidon首先提出DFP,又被Fletcher和Powell改进,定义校正矩阵为 p(k)p(k)Tp(k)Tq(k)−Hkq(k)q(k)THkq(k)THkq(k)
这样得到的矩阵为Hk+1=Hk+p(k)p(k)Tp(k)Tq(k)−Hkq(k)q(k)THkq(k)THkq(k)
输入:目标函数f(x),梯度g(x)=Δf(x),精度要求ϵ
输出:f(x)的极小点x∗
- step 1:取初始点x(0),取H0为正定对称矩阵,置k=0
- step 2:计算gk=g(x(k)),若||gk||≤ϵ,则停止计算,得近似解x∗=x(k);否则转step 3
- step 3:置pk=−Hkgk
- step 4:一维搜索:求λk使得f(x(k)+λkpk)=minf(x(k)+λpk),λ≥0
- step 5:置x(k+1)=x(k)+λkpk
- step 6:计算gk+1=g(x(k+1)),若||gk+1||<ϵ,则停止计算,得近似解x∗=x(k+1),否则,则计算出Hk+1
- step 7:置k=k+1,转step 3
疑问:怎么确定H0? https://www.zhihu.com/question/269123324/answer/345679876
3.2 BFGS
用不包含二阶导数的矩阵Bk近似代替牛顿法中的Hesse矩阵Gk。
Hk+1=B−1k+1
关于矩阵B的BFGS公式:
Bk+1=Bk+q(k)q(k)Tq(k)Tp(k)−Bkp(k)p(k)TBkp(k)TBkp(k)
输入:目标函数f(x),梯度g(x)=Δf(x),精度要求ϵ
输出:f(x)的极小点x∗
- step 1:取初始点x(0),取B0为正定对称矩阵,置k=0
- step 2:计算gk=g(x(k)),若||gk||≤ϵ,则停止计算,得近似解x∗=x(k);否则转step 3
- step 3:由Bkpk=−gk求出pk
- step 4:一维搜索:求λk使得f(x(k)+λkpk)=minf(x(k)+λpk),λ≥0
- step 5:置x(k+1)=x(k)+λkpk
- step 6:计算gk+1=g(x(k+1)),若||gk+1||<ϵ,则停止计算,得近似解x∗=x(k+1),否则,则计算出Bk+1
- step 7:置k=k+1,转step 3
关于矩阵H的BFGS公式:
HBFGSk+1=Hk+(1+q(k)THkq(k)p(k)Tq(k))p(k)p(k)Tp(k)Tq(k)−p(k)q(k)THk+Hkq(k)p(k)Tp(k)Tq(k)
这个重要公式是由Broyden,Fletcher,Goldfard和Shanno于1970年提出的,所以简称为BFGS
疑问:为什么BFGS会比DFP流行?https://www.zhihu.com/question/269123324/answer/345679876
BFGS有自动纠错功能
3.3 L-BFGS
在BFGS算法中,仍然有缺陷,比如当优化问题规模很大时,矩阵的存储和计算将变得不可行。为了解决这个问题,就有了L-BFGS算法。L-BFGS即Limited-memory BFGS。 L-BFGS的基本思想是只保存最近的m次迭代信息,从而大大减少数据的存储空间。对照BFGS,重新整理一下公式:
具体步骤参考:https://zhuanlan.zhihu.com/p/29672873
L-BFGS算法为什么快?https://www.zhihu.com/question/49418974/answer/155668749
四、共轭梯度法(Conjugate Gradient)
共轭:设A是对称正定矩阵,若Rn中的两个方向d(1)和d(2)满足d(1)TAd(2)=0,则称这两个方向关于A共轭,或称它们关于A正交
定理:对于二次凸函数,若沿一组共轭方向(非零向量)搜索,经有限步迭代必达到极小点。
共轭梯度法基本思想:把共轭性与最速下降法结合,利用已知点处的梯度构成一组共轭方向,并沿这组方向进行搜索,求出目标函数的极小点,根据共轭方向的基本性质,这种方法具有二次终止性。
4.1 FR
βj=||gi+1||2||gi||2
二次函数计算步骤:
step 1:给定初始点x(1),置k=1
step 2:计算gk=Δf(x(k)),若||gk||=0,则停止计算,得点¯x=x(k);否则,进行下一步
step 3:构造搜索方向,令d(k)=−gk+βk−1d(k−1),其中,当k=1时,βk−1=0时,计算因子βk−1
step 4:令x(k+1)=x(k)+λkd(d),计算步长λk=−gTkd(k)d(k)TAd(k)
step 5:若k=n,则停止计算,得点¯x=x(k+1);否则,置k:=k+1,返回step 2
任意凸函数计算步骤:
step 1:给定初始点x(1),允许误差epsilon>0,置y(1)=x(1),d(1)=Δf(y(1)),k=j=1
step 2:若||Δf(y(j))||<ϵ,则停止计算;否则,作一维搜索,求λj,求满足f(y(j)+λjd(j))=minλ>=0(y)
step 3:如果j<n,则进行step 4;否则,进行step 5
step 4:令d(j+1)=−Δf(y(j+1))+βjd(j),其中,βj=||Δf(y(j+1))||2||Δf(y(j))||2,置j:=j+1,转step 2
step 5:令x(k+1)=y(n+1),y(1)=x(k+1),d(1)=−Δf(y(1)),置j=1,k:=k+1,转step 2
4.2 PRP
βj=gTj+1(gj+1−gj)gTjgj
任意凸函数计算步骤:
step 1:给定初始点x(1),允许误差epsilon>0,置y(1)=x(1),d(1)=Δf(y(1)),k=j=1
step 2:若||Δf(y(j))||<ϵ,则停止计算;否则,作一维搜索,求λj,求满足f(y(j)+λjd(j))=minλ>=0(y)
step 3:如果j<n,则进行step 4;否则,进行step 5
step 4:令d(j+1)=−Δf(y(j+1))+βjd(j),其中,βj=gTj+1(gj+1−gj)gTjgj,置j:=j+1,转step 2
step 5:令x(k+1)=y(n+1),y(1)=x(k+1),d(1)=−Δf(y(1)),置j=1,k:=k+1,转step 2
共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
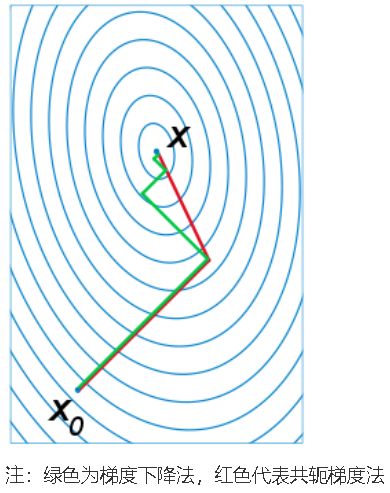
五、比较
梯度下降法和牛顿法的比较:
从本质来说,梯度下降法是一阶收敛,牛顿法是二阶收敛,所以牛顿法的收敛速度更快。梯度下降法每次考虑的是当前位置的负梯度下降,而牛顿法不但考虑当前位置下降的是否够快,还会考虑下一步下降的是否够大,也就是说牛顿法目标更长远一点。牛顿法是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法使用一个平面去拟合当前的局部曲面,通常情况二次曲面拟合会比平面更好,所以牛顿法的下降路径会更符合真实的最优下降路径。
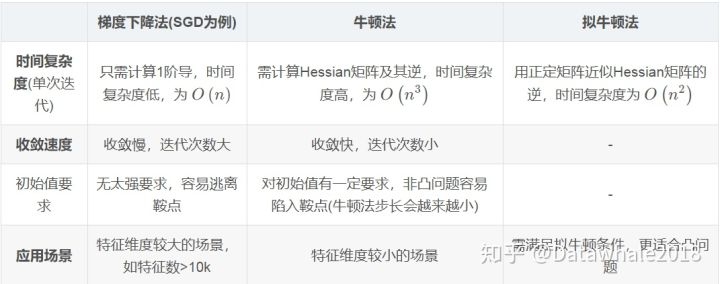 来源
来源
参考文献:
【1】常见的几种最优化方法(梯度下降法、牛顿法、拟牛顿法、共轭梯度法等)
【2】深度学习实战教程(二):线性单元和梯度下降
【3】梯度下降(Gradient Descent)小结
【4】https://www.jianshu.com/p/e8b5a384a970
【5】https://blog.csdn.net/philosophyatmath/article/details/70153705
【6】梯度下降法、牛顿法、拟牛顿法 三类迭代法应用场景有何差别?






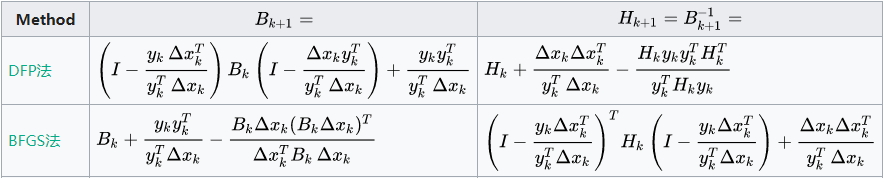





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现