模型融合---Adaboost总结简洁版
一、简介
这个方法主要涉及到2个权重集合：
样本的权重集合
每个样本都对应一个权重。 在构建第一个弱模型之前，所有的训练样本的权重是一样的。第一个模型完成后，要加大那些被这个模型错误分类(分类问题)、或者说预测真实差值较大(回归问题)的样本的权重。依次迭代，最终构建多个弱模型。每个弱模型所对应的训练数据集样本是一样的，只是数据集中的样本权重是不一样的。
弱模型的权重集合
得到的每个弱模型都对应一个权重。精度越高(分类问题的错分率越低，回归问题的错误率越低)的模型，其权重也就越大，在最终集成结果时，其话语权也就越大。
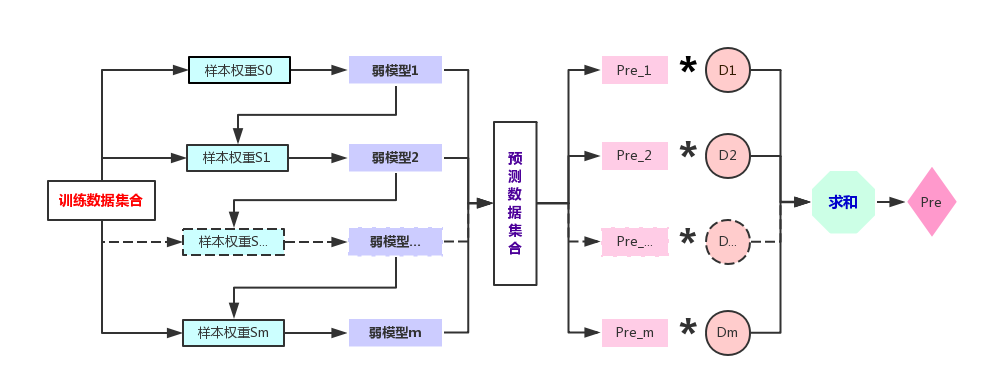
二、步骤
1.分类问题
- 训练数据集
令Yi = 1 or -1，这种定义便于后面的结果集成。集合Y0表示数据集样本的真实类别序列。
- 初始的样本权重集合S1，弱模型的权重集合为D
n为数据集样本个数，m为要建立的弱模型的个数
- 针对数据集构建弱模型M1，得到这个弱模型的错分率为
假设弱模型M1的训练数据集的预测类别序列为P1，预测数据集的预测类别序列为Pre_1。
，
其中Cerror表示被弱模型M1错分的样本个数，CData为全部的样本个数，也就是n。
- 计算弱模型M1的权重
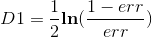
- 更改样本的权重
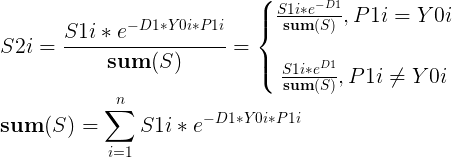
D1为非负数，因此预测正确的样本的权重会比上一次的降低，预测错误的会比上一次的增高。
其中除以sum(S)，相当于将样本权重规范化。
- 迭代
当达到设定的迭代次数时停止，或者错分率小于某个小的正数时停止迭代。
此时得到m个弱模型，以及预测数据集对应的预测结果序列Pre_1，Pre_2， ……Pre_m，
以及模型的权重集合D。
- 结果集成
针对第i个预测样本的集成结果为JI_i,
，sign为符号函数。
回归问题和分类问题的最大不同在于，回归问题错误率的计算不同于分类问题的错分率，下面给出回归问题的步骤，因为回归算法有很多的变种，这里以Adaboost R2算法为例说明：
2.回归问题
- 训练数据集
，输出值的序列为Y0。
- 初始的样本权重集合S1，弱模型的权重集合为D
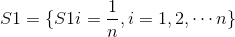
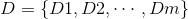
n为数据集样本个数，m为要建立的弱模型的个数
-
针对数据集构建弱模型M1，得到这个弱模型的错误率为
假设弱模型M1的训练数据集的预测类别序列为P1，预测数据集的预测类别序列为Pre_1。
-
误差损失为线性
-
误差损失为平方
-
误差损失为指数
错误率的计算公式为：
-
-
计算弱模型M1的权重
-
更改样本的权重
。 其中除以sum(S)，相当于将样本权重归一化。
-
迭代
当达到设定的迭代次数时停止，或者错误率小于某个小的正数时停止迭代。
此时得到m个弱模型，以及预测数据集对应的预测结果序列Pre_1，Pre_2， ……Pre_m，
以及模型的权重集合D。
-
结果集成
针对第i个预测样本的集成结果为JI_i,
3.正则化
现在将回归问题和分类问题的最终的集成形式写为如下更为一般的形式
也就是有：
现在将其正则化：
其中a为学习率，也就是步长。在调参时，和弱模型的最大个数一起调参。
三、疑点
- 增加的样本权重如何在下一个模型训练时体现出作用？
答：以决策树为例，计算最佳分割点基尼系数时，或者MSE时，要乘以样本权重。总之，对于样本的计算量，要乘以相应的样本的权重。如果没在这个AdaBoost的框架下，则相当于原来的样本的权重都是一样的，所以乘或者不乘是一样的，现在在这个AdaBoost的框架下，因为样本权重发生了改变，所以需要乘。这样就把样本权重的改变体现了出来。
- 这个弱模型可以是什么？
答：经常用的就是单层的决策树，也称为决策树桩(Decision Stump)，例如单层的CART。其实这个层数也是参数，需要交叉验证得到最好的。当然这个弱模型也可以是SVM、逻辑回归、神经网络等。
参考文献：
【1】Machine-Learning-for-Beginner-by-Python3/Boosting/AdaBoost/
