Oriented Response Networks 阅读笔记(一)
最近在arxiv上读到一篇很有意思的文章,题目叫“Oriented Response Networks ”,准备翻译一下。参考文献太多,就不一一粘过来了,
ORN文章阅读笔记
一、 摘要
深度卷积神经网络能够从图像中习得有效的表示,但是其处理局部和全局图像旋转的能力仍然有限。本文提出主动旋转滤波器(ARFs),能够主动旋转,并产生位置和方向明确编码的特征图。一个ARF作为一个虚拟滤波器组,包含了滤波器自己和滤波器不同版本的旋转。在反向传播期间,一个ARF从全部的旋转过的滤波器中收集误差并更新。使用ARF的DCNN,称为定向响应网络(Oriented Response Network,ORN),可以产生类内旋转不变深度特征,同时保持分类任务的类间区分度。由ORNs产生的定向响应(oriented response)同时可以被用于图像和目标的方向估计。在多种先进的DCNN架构,例如VGG,ResNet和STN,我们观察到,使用本文提出的ARFs替换原有的卷积滤波器,网络参数的数量显著减少,分类性能明显提升。本文在常用的几个基准测试中获得了最佳结果。
二、 引言
方向信息编码问题已经在手工设计的特征中广泛研究,例如Gabor 特征[15, 17],HOG[9]和SIFT[31]. 在深度卷积神经网络(DCNN)中,卷积与池化层的固有性质减轻了局部变化和扭曲的影响,然而,缺乏处理大图像旋转的能力限制了DCNN在许多视觉任务中的性能,如目标边界检测[16, 32],多方向目标检测[6],图像分类[20, 23]。
由于缺乏充分理解旋转的能力,对于DCNN,最直接提升性能的方法是“基于旋转学习”。[11, 47]卷积滤波器的可视化显示了对于同一张图像的不同旋转能够在底层、中层和较高层的滤波器中学习到多余的特征。比如,在VGG16模型中的第11层[10]。当目标中的部分是否旋转与目标本身有关联时,比如鸟的头与鸟的身体,这要求使用更多的滤波器学习目标每一个部分的不同取向的多种组合。在这种情况下,网络会放弃理解目标整体概念,转而学习其有识别力的部分以作最终决策[48]。“基于旋转学习”的策略需要大量网络参数以生成旋转冗余的滤波器,显著增加了训练时间与网络过拟合风险。此外,由于有限的实例被隐含地分割为不同子集,训练数据未被充分利用,增加了欠拟合的风险。为了解决这一问题,通常使用旋转训练样本等方法扩充数据。扩充训练集虽然提升了学习效果,但是通常造成网络参数与训练开销的同步增加。
在本文中,我们提出主动旋转滤波器(ARFs),利用定向响应卷积(ORConv)生成特征图,其定向通道明确编码判别模式的位置和方向信息。与常规滤波器相比,ARFs具有定义定向结构的额外维度。在卷积的过程中,每个ARF旋转并产生特征图,以从多个取向捕获感受野的响应,如图1所示。
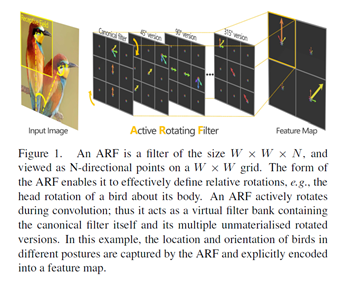
具有定向通道的特征图与分层网络一起进行定向响应以生成高级特征表示,赋予DCNNs捕获全局/局部旋转的能力以及对于之前从未见过的旋转样本的泛化能力。
不需要引入额外的功能模块或新的网络拓扑,我们的方法使用DCNNs中最基本的元素(即,卷积运算符)实现旋转的先验知识。因此,它可以自然地与现代DCNN架构融合,将其升级为更具表达性和紧凑的定向响应网络(ORN)。对于ORNs处理方向信息的过程,我们可以应用SIFT般的特征对齐以实现旋转不变性或执行图像/对象取向估计。本文的贡献总结如下:
- 本文提出主动旋转滤波器与定向响应卷积,改进了DCNN的最基本模块,并赋予DCNN显式编码分层定向信息的能力。我们进一步将这种取向信息应用于旋转不变图像分类和对象取向估计。
- 本文将成功的DCNN(包括VGG,ResNet,TI-Pooling和STN)升级到ORN,以实现最先进的性能,并在常用基准上显著减少网络参数。
三、 相关工作
3.1 手工特征
定向信息已经在传统手工制作特征中明确编码,包括韦伯定律描述符[5],Gabor特征[15,17],SIFT [31]和LBP [33,1]。 SIFT描述符[31]及其变种利用局部区域仿射[25]找到特征点的主方向,根据该特征点累积图像强度的局部梯度方向的统计以给出局部图像结构的概括描述。利用基于主方向的特征对齐,SIFT实现了对旋转的不变性和适度透视变换的鲁棒性[2,12]。从局部邻域中的圆形对称相邻像素集合的灰度值开始,LBP导出对于任何单调变换定义不变的算子的灰度[33,1]。通过使用比特循环移位来最小化LBP码值来实现旋转不变性。其他代表性描述符包括使用取向对齐的CF-HOG [39]和利用径向梯度变换的旋转不变的RI-HOG [30]。
3.2 深度卷积神经网络
深度卷积神经网络能够处理图像的形变、尺度变化、小的旋转。这种能力来自于卷积操作符、冗余的卷积核,层次空间池化(hierarchical spatial pooling)[35, 20]的固有属性。更多通用的赤化操作[26]允许考虑局部变形的不变性,但是不对应于特定的先验知识。
3.2.1 数据扩充
给定足够的、冗余的卷积核,数据扩充能够达到局部/全局的不变性[43]。尽管数据扩充很有效,主要问题是学习扩充后的数据的全部变换通常需要更多的网络参数,会显著增加训练开销与过拟合风险。最近的TI-Pooling[23]通过使用并行网络结构,在这些网络的输出端使用具有变换不变性的池化操作,改善了这个不足。
TI-Pooling的本质是包含多模板的学习与权值共享,能够帮助寻找输入图像最简洁的模板用于训练,降低网络学习的冗余。然而,由于TI-Pooling网络内部的数据扩充,比起DCNN,网络训练和测试开销显著提升。
3.2.2 Scatting Wavelet Network.
小波散射网络是一个变化不变的特征编码器,定义了2层网络,通过小波系数模的均值池化[3, 37],第一个网络输出类似于SIFT的特征描述符,第二个网络提供了补足的不变性信息用于分类。通过计算具有相同的小波卷积与平均模量池化的下一层的不变系数,平均信息损失能够从中得以恢复。
3.2.3 空间变换网络(Spatial Transform Network)
代表性地,空间变换器网络(STN)[20]引入了可以根据利用定位子CNN估计的变换矩阵来处理特征图的附加网络模块。 STN提供了空间变换的一般框架,但是关于如何通过CNN精确地估计复变换参数的问题仍然没有被很好地解决[14,34]。[21, 36]中,卷积限制玻尔兹曼机(C-RBM)引入transformation-aware滤波器,比如,它产生具有使用其特定图像变换的概念的滤波器。 从群论的角度来看,Cohen et al. [8]证明图像的空间变换可以反映在特征图和滤波器中,提供了本文工作的理论基础。 一些最近的工作[44,13]尝试旋转常规过滤器以实现纹理的旋转不变性和图像分类,然而,没有将常规过滤器升级到具有定向通道的多向过滤器,它们关于捕获分层和细微定向信息的能力仍然有限。



