聚类算法评价指标学习笔记
聚类算法评价指标学习笔记
本文列举常用聚类性能度量指标,并列出相应代码与参考资料
聚类性能度量大致分两类,一类将聚类结果与某个“参考模型”(reference model)进行比较,称为“外部指标”(external index);另一类是直接考察聚类结果而不利用任何参考模型,称为“内部指标”(internal index)。(机器学习,周志华)。本文主要针对聚类算法的外部指标做总结。
与分类不同,聚类算法获取的类别标签具有不确定性,不能直接基于ground truth获得类似于分类算法的错误率、召回率、精度等评价指标。聚类算法通常将样本两两配对,再做进一步计算与评价。通过聚类给出的簇划分为C,参考模型(ground truth)给出的簇划分为K,通常K与C给出的簇类别数量不相同。定义a, b, c, d如下:
a: 在C中属于同一类别且在K中属于同一类别的样本对数量
b: 在C中属于同一类别且在K中属于不同类别的样本对数量
c: 在C中属于不同类别且在K中属于同一类别的样本对数量
d: 在C中属于不同类别且在K中属于不同类别的样本对数量
记总样本数量为m,显而易见
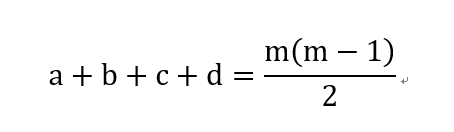
由上文可导出常用聚类性能度量外部指标:
- Jaccard 系数(Jaccard Coefficient,简称JC)
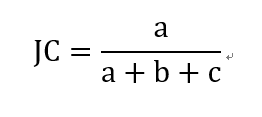
- FM指数(Fowlkes and Mallows Index,简称FMI)

- Rand指数(Rand Index,简称RI)
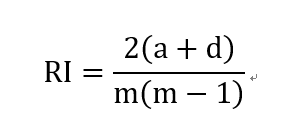
显然,上述性能度量的结果值均在 [0,1] 区间,值越大越好。
V-measure
V-measure 是同质性(homogeneity)和完整性(completeness)的调和平均数,
- 这个测度独立于label的绝对值,调整类别标签或聚类标签的值不会改变测度结果。
- 这个测度关于类别标签与聚类标签对称,交换类别标签与聚类标签不会使得测度结果发生变化。
- 当类别标签未知时,这种测度方法还可以用来比较两种标记策略的相似程度。
- V-measure取值在[0,1]区间内,值越大相似程度越高。
Mutual information
已知聚类标签与真实标签,互信息(mutual information)能够测度两种标签排列之间的相关性,同时忽略标签中的排列。有两种不同版本的互信息以供选择,一种是Normalized Mutual Information(NMI),一种是Adjusted Mutual Information(AMI)。比起最近才提出的AMI,更早提出的NMI更频繁地应用于文献中。
MI、NMI、AMI都是对称函数,交换变量不改变函数值,因此可以用做一致性检验。对于AMI与NMI,最佳的标签配对对应的函数值都是0,但是MI不是,这使得MI有时难以作为判断依据。
对于随机标签,通常会获得接近于0的AMI值。AMI的输出范围在[0,1]区间内,值越大表示相似程度越高。
基于MI的测度需要ground truth,在真实环境中ground truth需要大量手工标记,通常难以获得。但这并不意味着MI在无监督学习中一无是处。在纯的无监督学习中,基于MI的测度可以作为一致性指标的构建模块,用于聚类模型选择,用于纯无监督学习。
NMI与MI没有针对机会做调整(这个“机会”令我费解,要调研一下)。
基于MI的评价指标的数学公式
假设对于N个样本,存在两种标签分配策略,分别记做U,V。信息熵是一种信息不确定性的测度,定义如下:

其中 ![]() 表示从U中随机选取一个样本属于类别 U_i 的概率。同理有:
表示从U中随机选取一个样本属于类别 U_i 的概率。同理有:

其中 ![]() 。U和V的互信息计算公式如下:
。U和V的互信息计算公式如下:
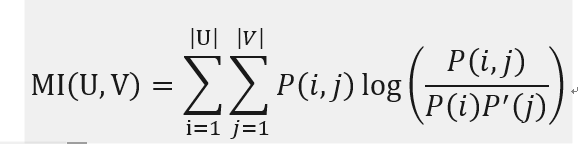
其中,![]() 是随机选取的样本同时属于U_i与V_j的概率。
是随机选取的样本同时属于U_i与V_j的概率。
NMI定义如下:

这个互信息的值经过了标准化,没有针对机会做调整(这个“机会”令我感到很费解,还需要学习),并且会随着聚类类别数量增加而增加,没有考虑不同的label分配方式之间的“互信息”的实际数量。
互信息的期望可以基于以下公式计算获得。(略)
AMI,调整后的互信息,定义如下:
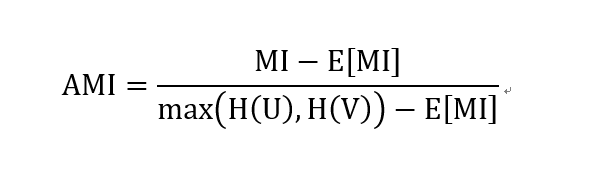
参考资料
scikit-learn模块中的MI指标说明(包括定义、公式、代码、例程等)
http://scikit-learn.org/stable/modules/clustering.html#mutual-information-based-scores




