二分类神经网络公式推导过程
简介:本文主要介绍了简单二分神经网络的公式推导过程。
欢迎探讨,如有错误敬请指正
如需转载,请注明出处 http://www.cnblogs.com/nullzx/
1. 数据表示说明
定义一个名为n的列表
n[i]表示第i层的节点数 i从0开始
L = len(n)-1表示神经网络的层数,网络的层数从第0层开始
W[i]的维度为(n[i], n[i-1]) i从1开始
b[i]的维度为(n[i], 1) i从1开始
2. 正向传播
X表示训练样本矩阵,每个训练样本有d个特征,有m个训练样本,所以X的维度是(d, m) 即n[0] = d
3. 交叉熵损失函数的推导过程
“*”表示对应元素相乘,![]() 表示第i个样本的真实值,
表示第i个样本的真实值,![]() 表示第i个样本的预测值,也就是神经网络最后一层的输出。
表示第i个样本的预测值,也就是神经网络最后一层的输出。
对于二分类的神经网络来说,最后一层的激活函数一般都是sigmoid函数
sigmoid函数由下列公式定义
从图中可知,最后一层的输出为0~1之间,可以看做概率。我们可以把二分神经网络看成一个概率模型,输入为一些特征,输出为概率,而且满足二项分布
![]() 表示真实值为0时,神经网络预测准确的概率,我们可以将上面的分段函数写成一个表达式
表示真实值为0时,神经网络预测准确的概率,我们可以将上面的分段函数写成一个表达式
所以上式表示了神经网络预测准确的概率。
当前有m个样本,那么like表示了这m个样本同时预测准确的概率
我们的目的就是让like取最大值,由于对数函数ln(x)是一个单调函数,所以当like函数取最大值时,ln(like)一定取得最大值
ln(like)取得最大值等价于下面的值取得最小。
而这个就是损失函数,初始化时w和b随机,我们通过随机梯度下降法,得到w和b使得损失函数最小。
另一方面,我们还可以通过信息论的角度推导交叉熵
4. 反向传播(随机梯度下降法)
L表示最后一层,从最后一层开始,由损失函数逐步向后求导
一般情况下
sigmoid的导数可以用自身表示:
![]() 一定是维度 (1, m)一个样本对应一列(也就是一个数值),
一定是维度 (1, m)一个样本对应一列(也就是一个数值),
假设已经知道了![]() ,它的维度是(n[i], m),则可以推出三点:
,它的维度是(n[i], m),则可以推出三点:
1)![]() ,它的维度是(n[i], m) 乘以(n[i-1], m)T
,它的维度是(n[i], m) 乘以(n[i-1], m)T
它的维度是(n[i+1], n[i]).T乘以(n[i+1], m)
同理还可以继续推出
*表示对应元素相乘,而![]() 就是激活函数的求导,这样就可以继续向下求导了
就是激活函数的求导,这样就可以继续向下求导了
5. 参数更新
k表示学习速度
6. 通过具体的例子解释反向传播的公式
对于上图神经网络的而言的一个训练样本而言,在求导的过程中我们应该把![]() 看成一个有关
看成一个有关![clip_image006[11] clip_image006[11]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095553239-1025670347.png) 的超多元函数
的超多元函数
我们从最后一层开始反向传播
注意最后推导出来的结果是两个矩阵的乘法
继续向前一层进行反向传播
维度(3,1)
因为
展开可得
现在将成本函数![]() 看成由
看成由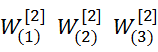 这12个自变量的函数(为啥是12个,因为每一个
这12个自变量的函数(为啥是12个,因为每一个![]() 都是一个1行4列的向量)
都是一个1行4列的向量)
这矩阵正好可以表示成
维度(3,1)乘 维度(4,1)T 形成一个(3,4)的矩阵
现在将成本函数![]() 看成由
看成由![]() 这4个自变量的函数(为啥是4个,因为
这4个自变量的函数(为啥是4个,因为![]() 是一个4行1列的向量)
是一个4行1列的向量)
这个矩阵恰好可以表示成
通用形式:
对于m个样本而言,我们求得的某个参数的导数是m样本分别对这个参数求导的平均值。至此反向传播过程推导推导完毕。
7. 参考内容
[1]. 浅谈神经网络算法


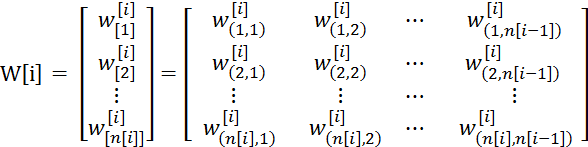
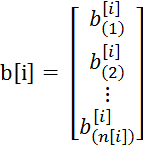
![clip_image002[6] clip_image002[6]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095458839-1499904374.png)
![clip_image002[8] clip_image002[8]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095505168-1120641895.png)
![clip_image008[5] clip_image008[5]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095509948-1220140923.png)
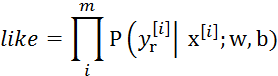
![clip_image002[14] clip_image002[14]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095515072-2127237803.png)
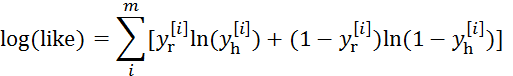
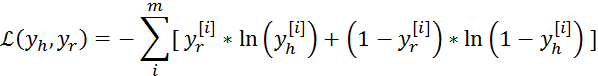
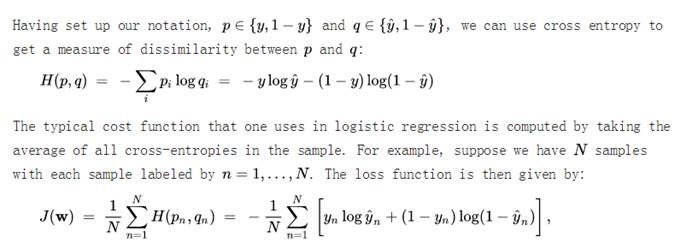
![clip_image002[10] clip_image002[10]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095520552-1506850794.png)
![clip_image004[9] clip_image004[9]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095522256-2114540507.png)
![clip_image002[12] clip_image002[12]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095537772-345494241.png)
![clip_image004[11] clip_image004[11]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095538958-31323872.png)
![clip_image002[16] clip_image002[16]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095549916-1174649450.png)
![clip_image014[7] clip_image014[7]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095558373-2144515746.png)
![clip_image016[6] clip_image016[6]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095559965-188813843.png)
![clip_image018[6] clip_image018[6]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095601892-1571189941.png)
![clip_image020[7] clip_image020[7]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095611003-939809823.png)
![clip_image022[6] clip_image022[6]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095612912-1666207567.png)
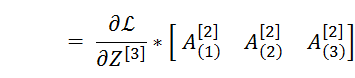
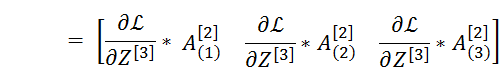
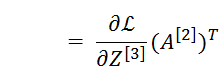
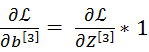
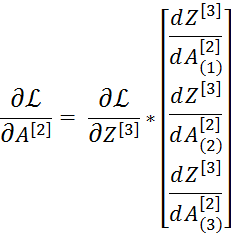
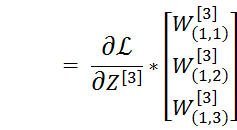
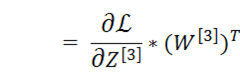
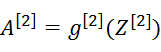
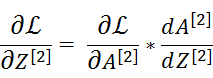

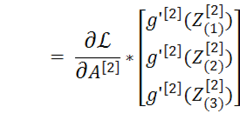
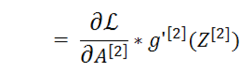
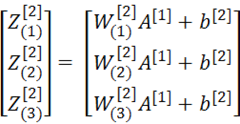
![clip_image002[18] clip_image002[18]](https://images2018.cnblogs.com/blog/834468/201806/834468-20180627095639057-1838392499.png)
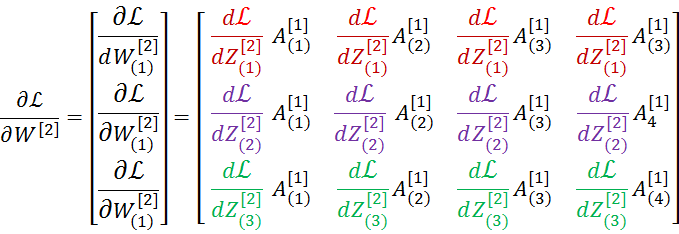
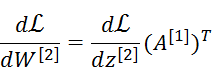
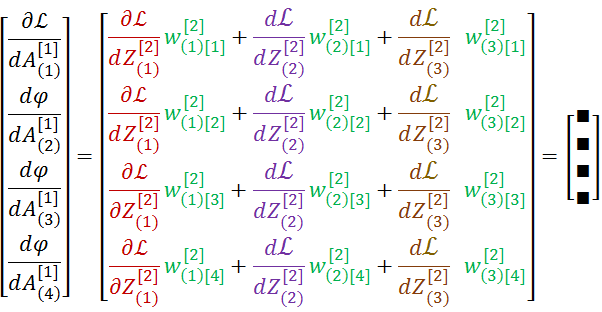
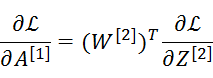
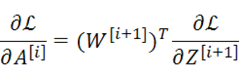

 浙公网安备 33010602011771号
浙公网安备 33010602011771号