Kosaraju算法解析: 求解图的强连通分量
欢迎探讨,如有错误敬请指正
如需转载,请注明出处 http://www.cnblogs.com/nullzx/
1. 定义
连通分量:在无向图中,即为连通子图。
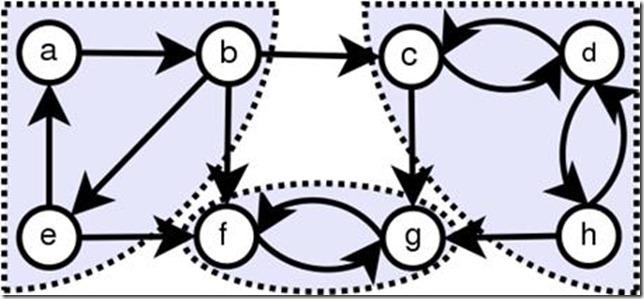
上图中,总共有四个连通分量。顶点A、B、C、D构成了一个连通分量,顶点E构成了一个连通分量,顶点F,G和H,I分别构成了两个连通分量。
强连通分量:有向图中,尽可能多的若干顶点组成的子图中,这些顶点都是相互可到达的,则这些顶点成为一个强连通分量。
上图中有三个强连通分量,分别是a、b、e以及f、g和c、d、h。
2. 连通分量的求解方法
对于一个无向图的连通分量,从连通分量的任意一个顶点开始,进行一次DFS,一定能遍历这个连通分量的所有顶点。所以,整个图的连通分量数应该等价于遍历整个图进行了几次(最外层的)DFS。一次DFS中遍历的所有顶点属于同一个连通分量。
下面我们将介绍有向图的强连通分量的求解方法。
3. Kosaraju算法的基本原理
我们用一个最简单的例子讲解Kosaraju算法
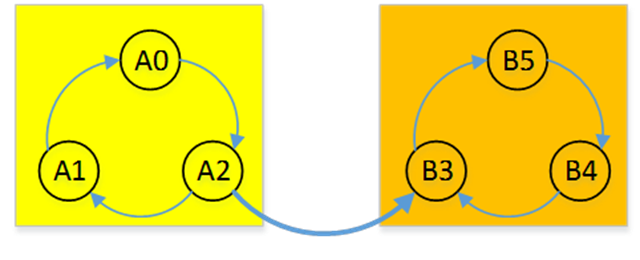
显然上图中有两个强连通分量,即强连通分量A和强连通分量B,分别由顶点A0-A1-A2和顶点B3-B4-B5构成。每个连通分量中有若干个可以相互访问的顶点(这里都是3个),强连通分量与强连通分量之间不会形成环,否则应该将这些连通分量看成一个整体,即看成同一个强连通分量。
我们现在试想能否按照无向图中求连通分量的思路求解有向图的强连通分量。我们假设,DFS从强连通分量B的任意一个顶点开始,那么恰好遍历整个图需要2次DFS,和连通分量的数量相等,而且每次DFS遍历的顶点恰好属于同一个连通分量。但是,我们若从连通分量A中任意一个顶点开始DFS,就不能得到正确的结果,因为此时我们只需要一次DFS就访问了所有的顶点。所以,我们不应该按照顶点编号的自然顺序(0,1,2,……)或者任意其它顺序进行DFS,而是应该按照被指向的强连通分量的顶点排在前面的顺序进行DFS。上图中由强连通分量A指向了强连通分量B。所以,我们按照
B3, B4, B5, A0, A1, A2
的顺序进行DFS,这样就可以达到我们的目的。但事实上这样的顺序太过严格,我们只需要保证被指向的强连通分量的至少一个顶点排在指向这个连通分量的所有顶点前面即可,比如
B3, A0, A1, A2, B4, B5
B3排在了强连通分量A所有顶点的前面。
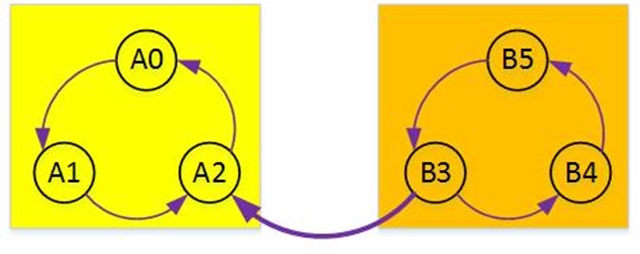
现在我们的关键问题就是如何得到这样一个满足要求的顶点顺序,Kosaraju给出了这解决办法:对原图取反,然后从反向图的任意节点开始进行DFS的逆后序遍历,逆后序得到的顺序一定满足我们的要求。
DFS的逆后序遍历是指:如果当前顶点未访问,先遍历完与当前顶点相连的且未被访问的所有其它顶点,然后将当前顶点加入栈中,最后栈中从栈顶到栈底的顺序就是我们需要的顶点顺序。
上图表示原图的反向。
我们现在进行第一种假设:假设DFS从位于强连通分量A中的任意一个节点开始。那么第一次DFS完成后,栈中全部都是强连通分量A的顶点,第二次DFS完成后,栈顶一定是强连通分量B的顶点。保证了从栈顶到栈底的排序强连通分量B的顶点全部都在强连通分量A顶点之前。
我们现在进行第二种假设:假设DFS从位于强连通分量B中的任意一个顶点开始。显然我们只需要进行一次DFS就可以遍历整个图,由于是逆后续遍历,那么起始顶点一定最后完成,所以栈顶的顶点一定是强连通分量B中的顶点,这显然是我们希望得到的顶点排序的结果。
上面使用了最简单的例子说明Kosaraju算法的原理,对于有多个强连通分量,连接复杂的情况,仍然适用。大家可以自行举例验证。
综上可得,不论从哪个顶点开始,图中有多少个强连通分量,逆后续遍历的栈中顶点的顺序一定会保证:被指向的强连通分量的至少一个顶点排在指向这个连通分量的所有顶点前面。所以,我们求解强连通分量的步骤可以分为两步:
(1)对原图取反,从任意一个顶点开始对反向图进行逆后续DFS遍历
(2)按照逆后续遍历中栈中的顶点出栈顺序,对原图进行DFS遍历,一次DFS遍历中访问的所有顶点都属于同一强连通分量。
4. 求解连通分量和强连通分量的代码实现
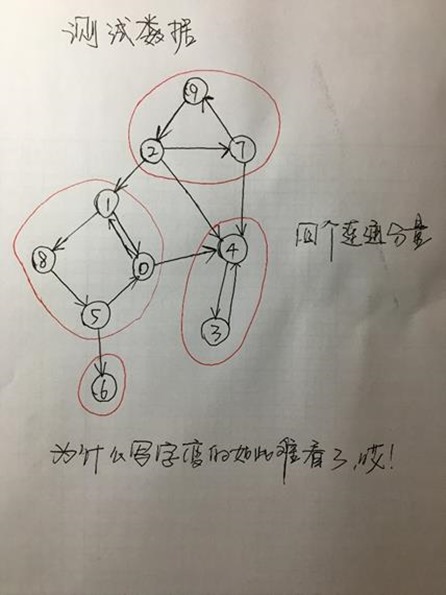
测试数据
|
10 15 0 1 0 4 1 0 1 8 2 1 2 4 2 7 3 4 4 3 5 0 5 6 7 9 7 4 8 5 9 2 |
运行结果
|
图的表示 0 : 1 4 1 : 0 8 2 : 1 4 7 3 : 4 4 : 3 5 : 0 6 6 : 7 : 9 4 8 : 5 9 : 2 连通分量数: 4 和顶点 0 共属于同一个连通分量的顶点 0 1 5 8 和顶点 3 共属于同一个连通分量的顶点 3 4 和顶点 9 共属于同一个连通分量的顶点 2 7 9 和顶点 6 共属于同一个连通分量的顶点 6 |
ConnectedComponents 包含了无向图求连通分量以及Kosaraju算法的实现
package datastruct;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.LinkedList;
import java.util.List;
import datastruct.Graph.Edge;
public class ConnectedComponents {
private boolean[] marked;
/*用于标记每个顶点属于哪一个(强)连通分量
同一(强)连通分量顶点的(强)连通分量编号值相同*/
private int[] id;
private int count;//(强)连通分量的编号,也表示(强)连通分量的个数
private Graph g;
public ConnectedComponents(Graph g){
this.g = g;
marked = new boolean[g.V()];
id = new int[g.V()];
if(g.isDirect()){//有向图求强连通分量的方法
//反向图DFS的逆后序,从0号顶点开始,可以从任意顶点开始
LinkedList<Integer> stack = g.reverse().reversePostOrder(0);
marked = new boolean[g.V()];
while(!stack.isEmpty()){
int v = stack.pop();
if(!marked[v]){
dfs(v);
count++;
}
}
}else{//无向图的连通分量
for(int i = 0; i < g.V(); i++){
if(!marked[i]){
dfs(i);
count++;
}
}
}
}
private void dfs(int v){
if(!marked[v]){
marked[v] = true;
id[v] = count;
for(Edge e : g.adjEdge(v)){
int w = e.other(v);
dfs(w);
}
}
}
public int count(){
return count;
}
//与顶点v属于同一连通分量的所有顶点
public List<Integer> allConnected(int v){
LinkedList<Integer> list = new LinkedList<Integer>();
int k = id[v];
for(int i = 0; i < g.V(); i++){
if(id[i] == k){
list.add(i);
}
}
return list;
}
public static void main(String[] args) throws FileNotFoundException{
File path = new File(System.getProperty("user.dir")).getParentFile();
File f = new File(path,"algs4-data/tinyDG2.txt");
FileReader fr = new FileReader(f);
Graph graph = new Graph(fr, true, false);
System.out.println("图的表示");
System.out.println(graph);
ConnectedComponents cc = new ConnectedComponents(graph);
System.out.println("连通分量数: " + cc.count());
System.out.println("\n");
System.out.println("和顶点 0 共属于同一个连通分量的顶点");
for(int i : cc.allConnected(0)){
System.out.printf("%-3d", i);
}
System.out.println("\n");
System.out.println("和顶点 3 共属于同一个连通分量的顶点");
for(int i : cc.allConnected(3)){
System.out.printf("%-3d", i);
}
System.out.println("\n");
System.out.println("和顶点 9 共属于同一个连通分量的顶点");
for(int i : cc.allConnected(9)){
System.out.printf("%-3d", i);
}
System.out.println("\n");
System.out.println("和顶点 6 共属于同一个连通分量的顶点");
for(int i : cc.allConnected(6)){
System.out.printf("%-3d", i);
}
System.out.println();
}
}
图的临接表示,包含了很多实用的方法,但是此处主要使用通过原图构造它的反方向图和逆后序
package datastruct;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.io.PrintWriter;
import java.io.Reader;
import java.io.StringWriter;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;
public class Graph{
private int v;//顶点数量
private int e;//边数量
private boolean isWeight; //时候是带权重的图
private boolean isDirect; //是否是有向图
private boolean hasCycle; //图中时候含有环
private LinkedList<Edge>[] adj;//临接表
//图中边的表示
public static class Edge implements Comparable<Edge>{
private final int from;//边起始顶点
private final int to;//边终结顶点
private final double w; //权值
public Edge(int from, int to, double w){
this.from = from;
this.to = to;
this.w = w;
}
//返回任意一个顶点
public int either(){
return from;
}
//返回另一个顶点
public int other(int v){
return v == this.from ? to : from;
}
//用于有向图
public int from(){
return from;
}
//用于有向图
public int to(){
return to;
}
public double weight(){
return w;
}
//边比较器,已权重为依据
@Override
public int compareTo(Edge that) {
if(this.w > that.w){
return 1;
}else
if(this.w < that.w){
return -1;
}else{
return 0;
}
}
//边的显示方法
@Override
public String toString(){
return new String(String.format("%-2d", from) + " "
+ String.format("%-2d", to) + " "
+ String.format("%-4.2f", w));
}
}
// public static class Cmp implements Comparator<Edge>{
// @Override
// public int compare(Edge e1, Edge e2) {
// return e1.compareTo(e2);
// }
// }
//从文件流中读入图的txt文件来构造图
@SuppressWarnings("unchecked")
public Graph(Reader r, boolean isDirect, boolean isWeight){
BufferedReader br = new BufferedReader(r);
Scanner scn = new Scanner(br);
v = scn.nextInt();
e = scn.nextInt();
this.isWeight = isWeight;
this.isDirect = isDirect;
adj = (LinkedList<Edge>[])new LinkedList[v];
for(int i = 0; i < v; i++){
adj[i] = new LinkedList<Edge>();
}
for(int i = 0; i < e; i++){
int from = scn.nextInt();
int to = scn.nextInt();
double w;
if(isWeight){
w = scn.nextDouble();
}else{//如果不是带权重的图,默认权重是1
w = 1;
}
Edge e = new Edge(from, to, w);
adj[from].add(e);
if(!isDirect){
adj[to].add(e);
}
}
scn.close();
}
//当前图的反向图构造函数
@SuppressWarnings("unchecked")
private Graph(Graph g){
v = g.V();
e = g.E();
this.isWeight = g.isWeight;
this.isDirect = g.isDirect;
hasCycle = g.hasCycle;
adj = (LinkedList<Edge>[]) new LinkedList[v];
for(int i = 0; i < v; i++){
adj[i] = new LinkedList<Edge>();
}
for(int from = 0; from < v; from++){
for(Edge e : g.adj[from]){
int to = e.other(from);
double w = e.weight();
adj[to].add(new Edge(to, from, w));
}
}
}
//返回当前图的反向图
public Graph reverse(){
if(this.isDirect){
return new Graph(this);
}else{
throw new IllegalArgumentException("Graph is not Directed");
}
}
//通过添加边来构造图的构造函数
@SuppressWarnings("unchecked")
public Graph(int v, boolean isDirect, boolean isWeight){
adj = (LinkedList<Edge>[])new LinkedList[v];
for(int i = 0; i < v; i++){
adj[i] = new LinkedList<Edge>();
}
this.isDirect = isDirect;
this.isWeight = isWeight;
this.v = v;
}
//添加一条边
public void addEdge(Edge e){
adj[e.from].add(e);
this.e++;
if(!isDirect){
this.e++;
adj[e.to()].add(e);
}
}
//返回图中顶点个数
public int V(){
return v;
}
//返回图中边的数量
public int E(){
return e;
}
//邻接顶点,返回与顶点v相邻的所有顶点的编号
public List<Integer> adjVertex(int v){
ArrayList<Integer> list = new ArrayList<Integer>(adj[v].size());
for(Edge e : adj[v]){
list.add(e.other(v));
}
return list;
}
//返回与顶点v相邻的边,对于位于同一包中的类,这个方法效率更高
public List<Edge> adjEdge(int v){
return adj[v];
}
//返回一条边
public Edge getEdge(int from, int to){
for(Edge e : adj[from]){
if(e.other(from) == to){
return e;
}
}
return null;
}
//是否是有向图
public boolean isDirect(){
return isDirect;
}
//是否是带权重的图
public boolean isWeight(){
return isWeight;
}
//是否是有向无有环图
public boolean isDAG(){
if(!isDirect){
return false;
}
boolean[] marked = new boolean[v];
boolean[] onStack = new boolean[v];
for(int i = 0; i < v; i++){
if(!marked[i]){
dfs(i, marked, onStack);
}
}
return !hasCycle;
}
//用于判断DAG的深度优先遍历
private void dfs(int v, boolean[] marked, boolean[] onStack){
if(hasCycle){
return;
}
marked[v] = true;
onStack[v] = true;
for(Edge e : adj[v]){
int w = e.other(v);
if(!marked[w]){
dfs(w, marked, onStack);
}else
if(onStack[w]){
hasCycle = true;
return;
}
}
onStack[v] = false;
}
//图的显示方法
public String toString(){
StringWriter sw = new StringWriter(5*v + 10*e);//长度不是一个准确值,是尽量往大估计的
PrintWriter pw = new PrintWriter(sw);
for(int i = 0; i < v; i++){
pw.printf("%-3d: ", i);
for(Edge e : adj[i]){
if(isWeight){
pw.printf("[%-3d, %-4.2f] ", e.other(i), e.w);
}else{
pw.printf("%-3d ", e.other(i));
}
}
pw.println();
}
return sw.getBuffer().toString();
}
//是否存在从from到to的边
// public boolean hasEdge(int from, int to){
// boolean[] marked = new boolean[v];
// hasEdge0(from, to, marked);
// return marked[to];
// }
//
// private void hasEdge0(int from, int to, boolean[] marked){
// if(!marked[from]){
// marked[from] = true;
// for(Edge e : adj[from]){
// if(!marked[to]){
// hasEdge0(e.other(from), to, marked);
// }else{
// return;
// }
// }
// }
// }
//从from节点开始逆后序遍历,返回逆后序的栈
public LinkedList<Integer> reversePostOrder(int from){
LinkedList<Integer> stack = new LinkedList<Integer>();
boolean[] marked = new boolean[v];
for(int i = 0; i < v; i++){
reversePostOrderTar(i, stack, marked);
}
return stack;
}
//用于逆后序的深度优先遍历
private void reversePostOrderTar(int from, LinkedList<Integer> stack, boolean[] marked){
if(!marked[from]){
marked[from] = true;
for(Edge e : adj[from]){
reversePostOrderTar(e.other(from), stack, marked);
}
stack.push(from);
}
}
public static void main(String[] args) throws FileNotFoundException{
File path = new File(System.getProperty("user.dir")).getParentFile();
File f = new File(path, "algs4-data/tinyDG.txt");
FileReader fr = new FileReader(f);
Graph g = new Graph(fr, true, false);
System.out.println(g.toString());
System.out.println(g.reverse().toString());
// System.out.println(g.hasEdge(0, 7));
}
}
5. 参考内容
[1]. 算法(第4版)Robert Sedgewick 人民邮电出版社




 浙公网安备 33010602011771号
浙公网安备 33010602011771号