310. Minimum Height Trees
原题链接
题目描述
树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
示例 1:

输入:n = 4, edges = [[1,0],[1,2],[1,3]]
输出:[1]
解释:如图所示,当根是标签为 1 的节点时,树的高度是 1 ,这是唯一的最小高度树。
示例 2:
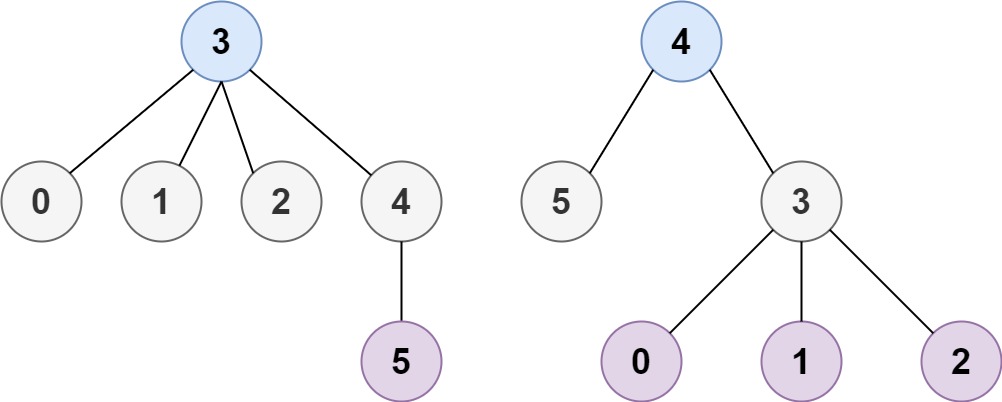
输入:n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出:[3,4]
示例 3:
输入:n = 1, edges = []
输出:[0]
示例 4:
输入:n = 2, edges = [[0,1]]
输出:[0,1]
问题分析
使用BFS
简单分析过程:
首先,我们看了样例,发现这个树并不是二叉树,是多叉树。
然后,我们可能想到的解法是:根据题目的意思,就挨个节点遍历bfs,统计下每个节点的高度,然后用map存储起来,后面查询这个高度的集合里最小的就可以了。
但是这样会超时的。
于是我们看图(题目介绍里面的图)分析一下,发现,越是靠里面的节点越有可能是最小高度树。
所以,我们可以这样想,我们可以倒着来。
我们从边缘开始,先找到所有出度为1的节点,然后把所有出度为1的节点进队列,然后不断地bfs,最后找到的就是两边同时向中间靠近的节点,那么这个中间节点就相当于把整个距离二分了,那么它当然就是到
两边距离最小的点啦,也就是到其他叶子节点最近的节点了。
class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
if(n == 1) return {0};
vector<int> degree(n, 0); //每个结点的度
map<int, vector<int>> m; //邻接表
vector<int> res; //结果
queue<int> q;
//初始化degree和m
for(auto e : edges){
degree[e[0]]++;
degree[e[1]]++;
m[e[0]].push_back(e[1]);
m[e[1]].push_back(e[0]);
}
//叶子结点入队
for(int i = 0; i < n; i++){
if(degree[i] == 1){//度为1,说明是叶子结点
q.push(i);
}
}
//从外向内一层一层剥,每次加入的都是一层
while(!q.empty()){
res.clear();
int level_size = q.size();
for(int i = 0; i < level_size; i++){
int t = q.front(); q.pop();
res.push_back(t);
degree[t]--;
for(auto neighbor : m[t]){
degree[neighbor]--;
if(degree[neighbor] == 1){//变成了叶子结点
q.push(neighbor);
}
}
}
}
return res;
}
};


