算法篇5：排序算法 （三种非比较排序算法）

一：前言

　　与前几种比较算法不同，今天要写的这几种算法都是非比较排序算法，分别是：桶排序，计数排序，基数排序。什么叫非比较排序呢？前面的几种算法都是通过 > 或者< 来进行排序，而非比较排序则是不通过两个数的大小比较来排序。非比较排序有其局限性，所以不常用，但是也有些情况他们是比比较排序快的。

二：具体实现

九：计数排序

 基本思路：

计数排序及对应每个数我们统计每个数字出现的次数，然后用一个直接定址的哈希表来存放数据，在通过遍历这个哈希表，进而就可以排好序了。

举例说明：

　　初始需排序数组 int[] arr = {6,3,8,6,3,1,3};

1：初始数组在0—8之间，最大为8，于是我们再定义一个长度为8+1=9的数组 count[] 初始化全为0；

2：遍历数组arr[]

3：第一个数为 6 ,则  count[ 6] +1=1；

4：第二个数为 3 ,则  count[ 3] +1=1；

5：第三个数为 8 ,则  count[ 8] +1=1；

6：第四个数为 6 ,则  count[ 6] +1=2；

7：第五个数为 3 ,则  count[ 3] +1=2；

8：第六个数为 1 ,则  count[ 1] +1=1；

9：第七个数为 3 ,则  count[ 3] +1=3；

10：遍历数组count 还原排序 { 1，3，3，3，6，6，8}

代码实现：

package com.xqc.sort;

import java.util.Arrays;

public class CountSort {
    
    public static void main(String[] args)
    {
        //初始化数组
        int[] A=new int[]{6,3,8,6,3,1,3};
        //打印
        System.out.println("排序前数组为："+Arrays.toString(A));
        //计数排序
        int[] B=countSort(A, 8);
        //打印
        System.out.println("排序后数组为："+Arrays.toString(B));
    }

    private static int[] countSort(int[] array,int k)
    {
        int[] count=new int[k+1];//构造count数组
        int length=array.length,sum=0;//获取A数组大小用于构造B数组  
        int[] B=new int[length];//构造B数组
        for(int i=0;i<length;i++)
        {
            count[array[i]]+=1;// 统计A中各元素个数，存入C数组
        }
        for(int i=0;i<k+1;i++)//修改C数组
        {
            sum+=count[i];
            count[i]=sum;    
        }
        for(int i=length-1;i>=0;i--)//遍历A数组，构造B数组
        {
            
            B[count[array[i]]-1]=array[i];//将A中该元素放到排序后数组B中指定的位置
            count[array[i]]--;//将C中该元素-1，方便存放下一个同样大小的元素
            
        }
        return B;//将排序好的数组返回，完成排序
        
    }
}

 

十：基数排序

基本思路：

　　举例说明：

1：初始化数组 int arr [] = { 73, 22, 93, 43, 55, 14, 28, 65, 39, 81}

2：首先根据个位，我们分了10个桶0—9，遍历数组分配如下（有顺序的填入）

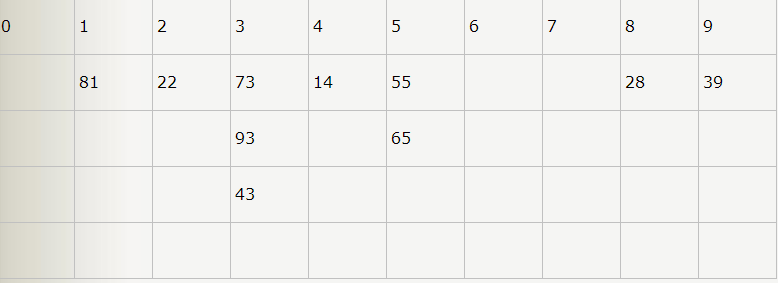
　　3：复原（有顺序的取出）数组为{ 81,22,73,93,43,14,55,65,28,39 } 

4：然后根据十位，我们又分了0—9共10个桶，遍历数组以此填入如下

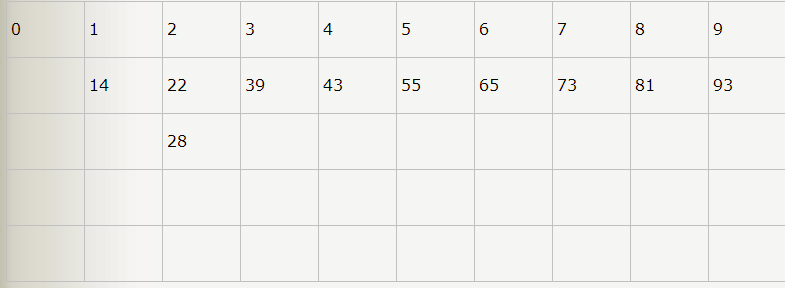
5：复原数组为  { 14,22,28,39,43,55,65,73,81,93 } 

6：这时就已经排好序了。

代码实现：

package com.xqc.sort;

import java.util.Arrays;

public class RadixSort {
    
    public static void main(String[] args)
    {
        int[] A=new int[]{73,22, 93, 43, 55, 14, 28, 65, 39, 81};
        //打印
        System.out.println("排序前数组为："+Arrays.toString(A));
        //基数排序
        radixSort(A, 100);
        //打印
        System.out.println("排序后数组为："+Arrays.toString(A));

    }
    
    private static void radixSort(int[] array,int d)
    {
        int n=1;//代表位数对应的数：1,10,100...
        int k=0;//保存每一位排序后的结果用于下一位的排序输入
        int length=array.length;
        int[][] bucket=new int[10][length];//排序桶用于保存每次排序后的结果，这一位上排序结果相同的数字放在同一个桶里
        int[] order=new int[length];//用于保存每个桶里有多少个数字
        while(n<d)
        {
            for(int num:array) //将数组array里的每个数字放在相应的桶里
            {
                int digit=(num/n)%10;
                bucket[digit][order[digit]]=num;
                order[digit]++;
            }
            for(int i=0;i<length;i++)//将前一个循环生成的桶里的数据覆盖到原数组中用于保存这一位的排序结果
            {
                if(order[i]!=0)//这个桶里有数据，从上到下遍历这个桶并将数据保存到原数组中
                {
                    for(int j=0;j<order[i];j++)
                    {
                        array[k]=bucket[i][j];
                        k++;
                    }
                }
                order[i]=0;//将桶里计数器置0，用于下一次位排序
            }
            n*=10;
            k=0;//将k置0，用于下一轮保存位排序结果
        }
        
    }

}

三：利用桶排序思想解决问题

问题：

 给定一个数组，求如果排序之后，相邻两数的最大差值。

思路分析：

 设计桶多一个，排除最大差值来自同一个桶，则最大差值肯定来自于相邻两个非空桶的最大值与最小值之差，然后我们将所有这些桶的差值计算出来，找到最大值即可。

 

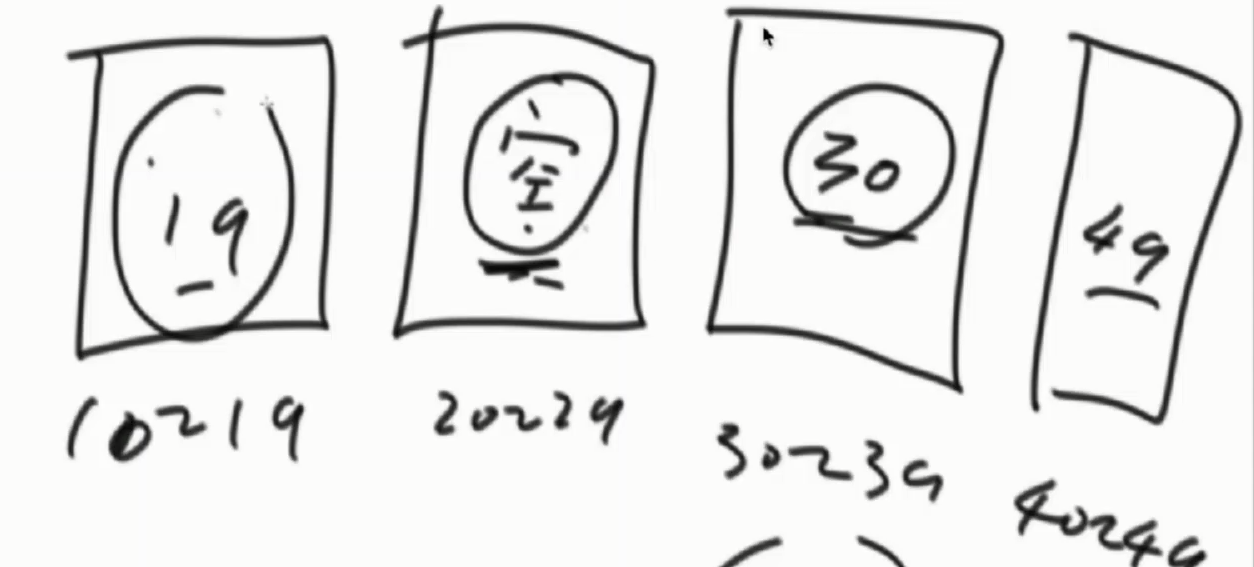
代码实现：

 

    public static int maxGap(int[] nums) {
        //如果数组为空或者为一没有最大差值
        if (nums == null || nums.length < 2) {
            return 0;
        }
        
        int len = nums.length;
        int min = Integer.MAX_VALUE;
        int max = Integer.MIN_VALUE;
        //遍历整个数组，找到最小值和最大值
        for (int i = 0; i < len; i++) {
            min = Math.min(min, nums[i]);
            max = Math.max(max, nums[i]);
        }
        //最小等于最大，则数组全是一种数
        if (min == max) {
            return 0;
        }
        //各个桶是否有数进入
        boolean[] hasNum = new boolean[len + 1];
        //各个桶的最大值
        int[] maxs = new int[len + 1];
        //各个桶的最小值
        int[] mins = new int[len + 1];
        
        int bid = 0;
        for (int i = 0; i < len; i++) {
            //进桶，更新桶信息
            bid = bucket(nums[i], len, min, max);
            mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i];
            maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i];
            hasNum[bid] = true;
        }
        int res = 0;
        int lastMax = maxs[0];
        int i = 1;
        //找个非空桶与左边的非空桶，用当前最小减去左边最大即为差值
        for (; i <= len; i++) {
            if (hasNum[i]) {
                res = Math.max(res, mins[i] - lastMax);
                lastMax = maxs[i];
            }
        }
        return res;
    }

    public static int bucket(long num, long len, long min, long max) {
        return (int) ((num - min) * len / (max - min));
    }