算法篇2：排序算法（中篇）

六：归并排序

基本思路：

将每条记录看成一个有序的子表，然后将有序表进行合并排序，直至完全有序

举例说明：

初始需排序数组：int[] arr = {6,3,8,2,9,1}

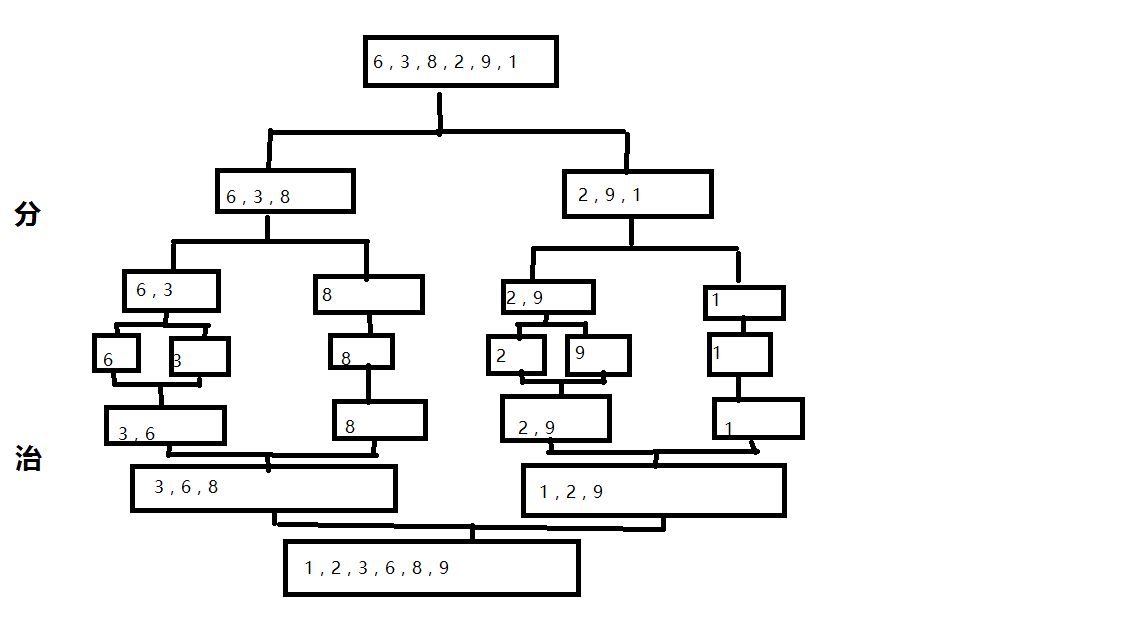
代码实现：

package com.xqc.sort;

import java.util.Arrays;

public class MergeSort {
    public static void main(String []args){
        //步骤1：初始化数组
        int[] arr={6,3,8,2,9,1};
        System.out.println("排序前数组为："+Arrays.toString(arr));
        //步骤二：归并排序
        int []temp = new int[arr.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        mergesort(arr,0,arr.length-1,temp);
        //步骤三：输出排序后数组
        System.out.println("排序后数组为："+Arrays.toString(arr));
    }
    private static void mergesort(int[] arr,int left,int right,int []temp){
        if(left<right){
            int mid = (left+right)/2;
            mergesort(arr,left,mid,temp);//左边归并排序，使得左子序列有序
            mergesort(arr,mid+1,right,temp);//右边归并排序，使得右子序列有序
            merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
        }
    }
    private static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i = left;//左序列指针
        int j = mid+1;//右序列指针
        int t = 0;//临时数组指针
        while (i<=mid && j<=right){
            if(arr[i]<=arr[j]){
                temp[t++] = arr[i++];
            }else {
                temp[t++] = arr[j++];
            }
        }
        while(i<=mid){//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while(left <= right){
            arr[left++] = temp[t++];
        }
    }
}

注：将有序表合并的简单图解（前两天刚看到别人画的，很好，盗图  https://www.cnblogs.com/chengxiao/p/6194356.html），即上述代码中的   merge（）方法

 

 

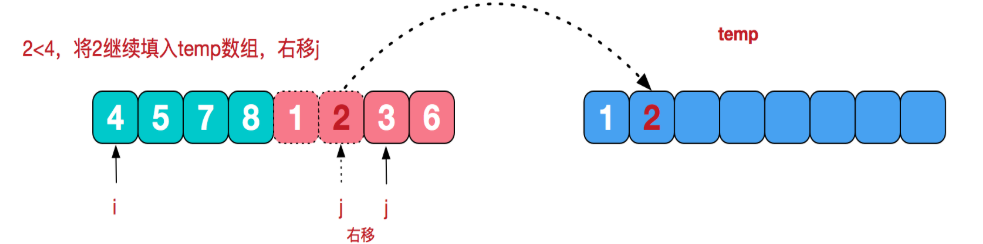
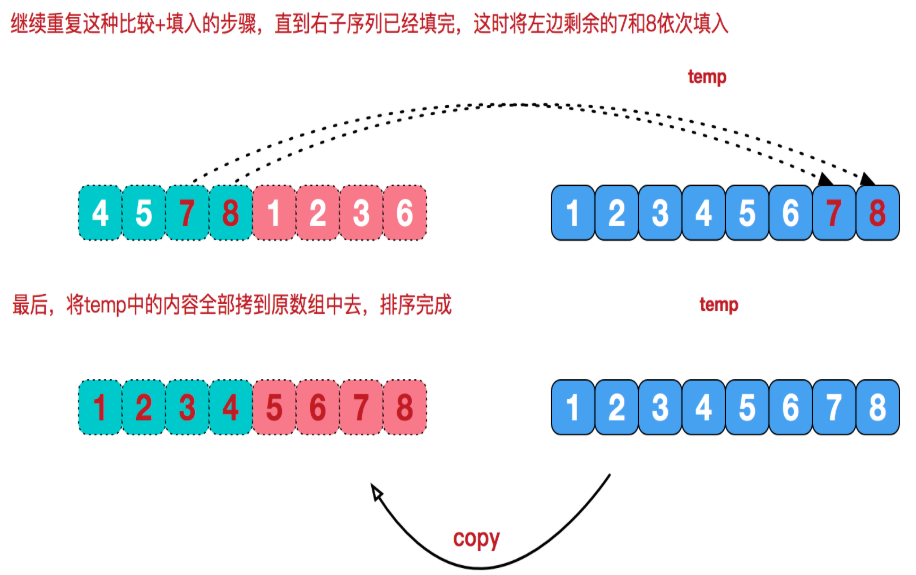
七：堆排序

 　　堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，堆分为两种，大根堆和小根堆，大根堆的要求是每个节点的值都不大于其父节点的值，小根堆则相反

 基本思路：

先构造出来大根堆（假设从小到大排序），然后取出堆顶元素（也就是最大的元素），放到数组的最后面，然后再将剩余的元素构造大根堆，再取出堆顶元素放到数组倒数第二个位置，依次类 推，知道所有的元素都放到数组中，排序就完成了

注：升序排序建立大根堆，降序排列建立小根堆

举例说明：

（原图出处：https://blog.csdn.net/qq_21492635/article/details/73105580）

初始化堆：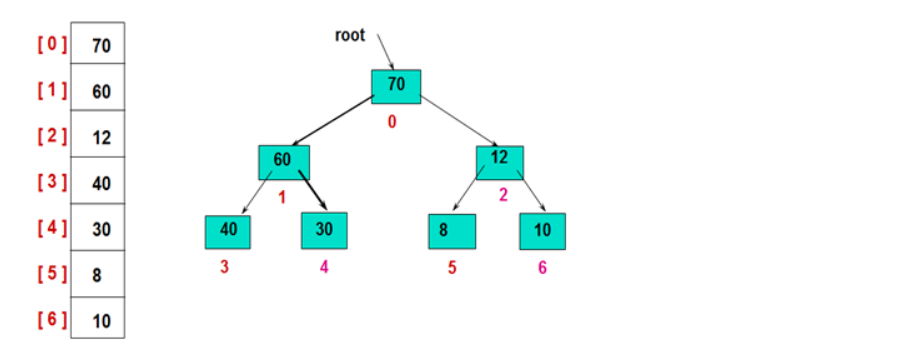

堆排序处理：

 

 

 

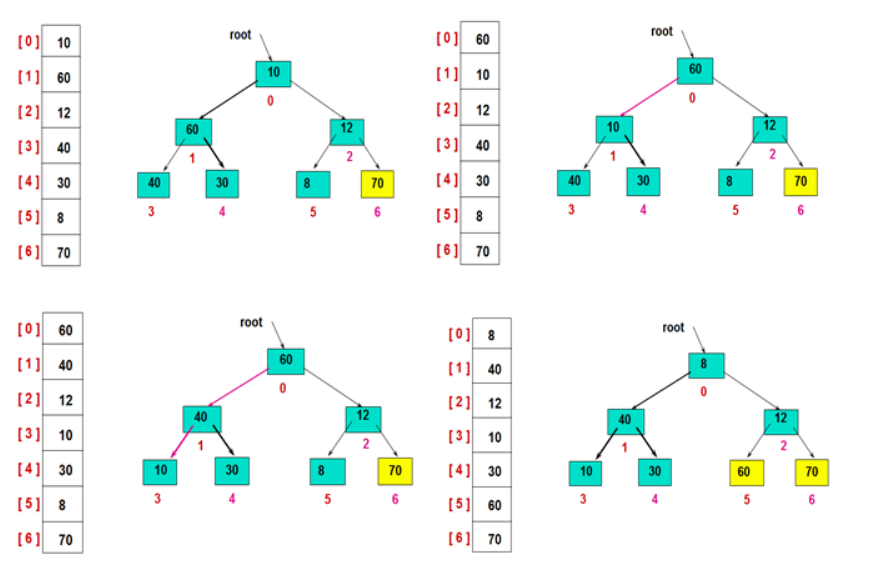
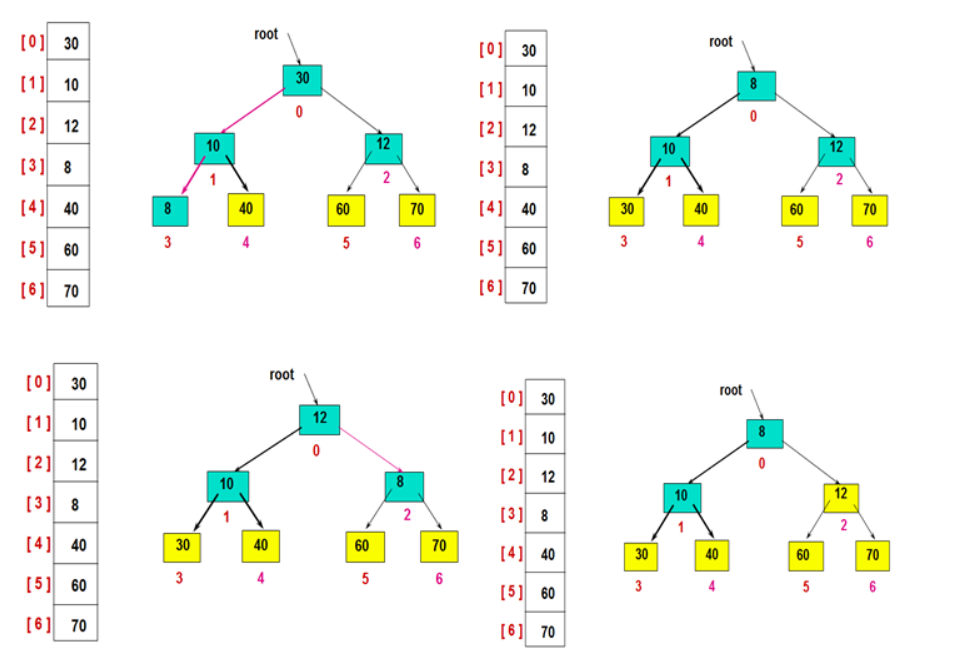
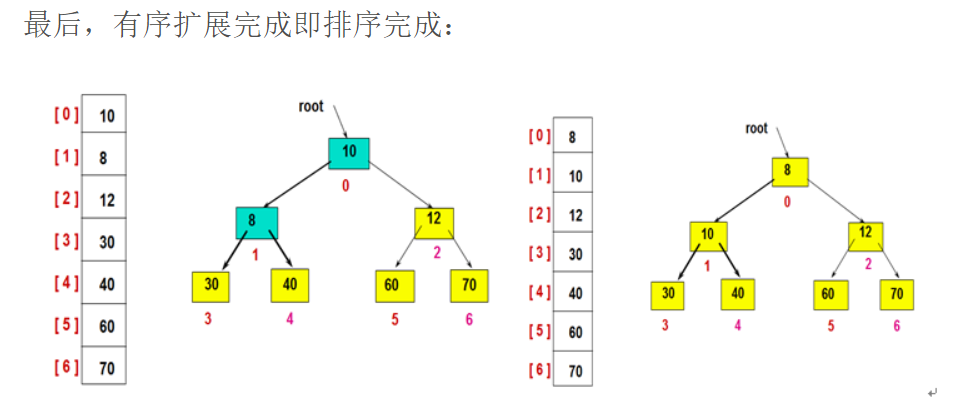
代码实现：

package com.xqc.sort;

import java.util.Arrays;

public class HeapSort
{
    public static void main(String[] args)
    {
        //步骤1：初始化数组
        int[] arr={6,3,8,2,9,1};
        System.out.println("排序前数组为："+Arrays.toString(arr));
        //步骤二：堆排序
        HeapSortFaction(arr);
        //步骤三：显示排序后数组
        System.out.println("排序后数组为："+Arrays.toString(arr));
    }
    //堆排序函数
    public static void HeapSortFaction(int[] arr)
    {
        int n = arr.length-1;
        for(int i=(n-1)/2;i>=0;i--)
        {
            //构造大顶堆，从下往上构造
            //i为最后一个根节点，n为数组最后一个元素的下标
            HeapAdjust(arr,i,n);
        }
        for(int i=n;i>0;i--)
        {
            //把最大的数，也就是顶放到最后
            //i每次减一，因为要放的位置每次都不是固定的
            swap(arr,i);
            //再构造大顶堆
            HeapAdjust(arr,0,i-1);
        }
    }

    //构造大顶堆函数，parent为父节点，length为数组最后一个元素的下标
    public static void HeapAdjust(int[] arr,int parent,int length)
    {
        //定义临时变量存储父节点中的数据，防止被覆盖
        int temp = arr[parent];
        //2*parent+1是其左孩子节点
        for(int i=parent*2+1;i<=length;i=i*2+1)
        {
            //如果左孩子大于右孩子，就让i指向右孩子
            if(i<length && arr[i]<arr[i+1])
            {
                i++;
            }
            //如果父节点大于或者等于较大的孩子，那就退出循环
            if(temp>=arr[i])
            {
                break;
            }
            //如果父节点小于孩子节点，那就把孩子节点放到父节点上
            arr[parent] = arr[i];
            //把孩子节点的下标赋值给parent
            //让其继续循环以保证大根堆构造正确
            parent = i;
        }
        //将刚刚的父节点中的数据赋值给新位置
        arr[parent] = temp;
    }

    //定义swap函数
    //功能：将跟元素与最后位置的元素交换
    //注意这里的最后是相对最后，是在变化的
    public static void swap(int[] arr,int i)
    {
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;
    }
}