数据结构基础认知（上）

这里只写一些基本概念，对数据结构中的一些名词做基本解释，以后所有的代码实现和算法实现都会再出新篇

一：绪论

1：常用的数据结构

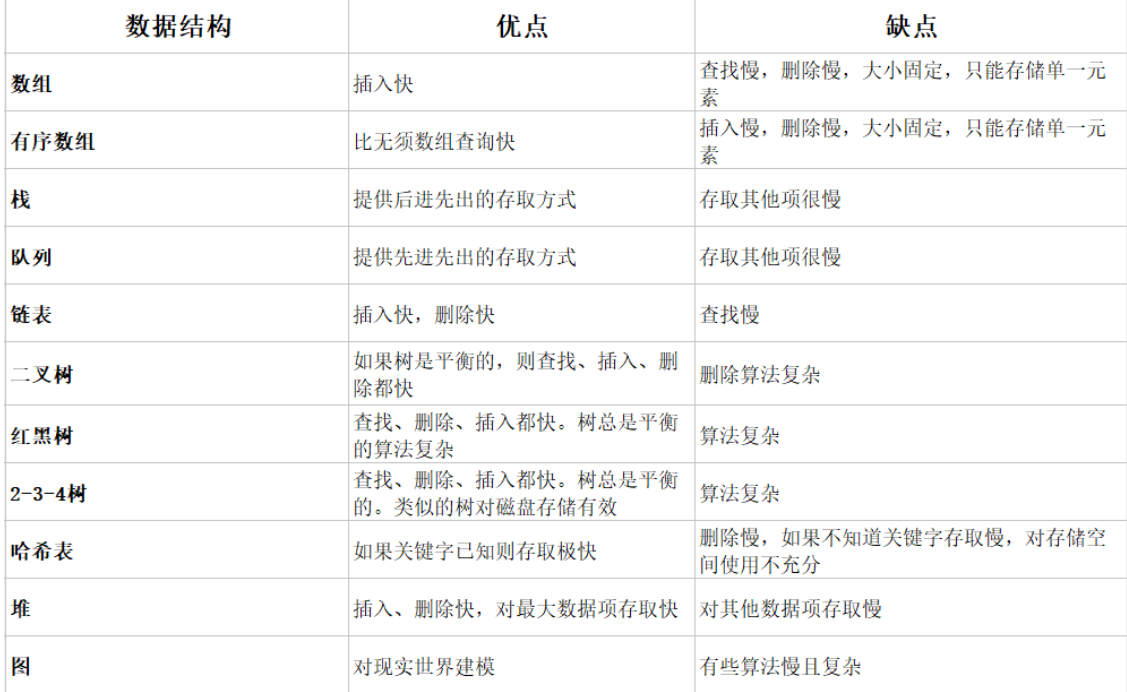
　　数组（Array），栈（Stack），队列（Queue），链表（Linked List） 树（Tree） 哈希（Hash），堆（Heap），图（Graph）

2：算法

1：数据的逻辑结构：集合，线性，树形，图

2：数据的存储（物理）结构：顺序存储，链式存储

3：算法的五大特性：有穷性，确定性，可行性，输入，输出

　　评价算法优劣的基本标准：正确性，可读性，健壮性，高效性

4：时间复杂度：

O(1) < O(log2n) < O(n) < O(n²）<O(n³) ····<O(n!)

递归复杂度的计算：

 

5：空间复杂度

6：抽象数据类型的表示：Status（函数返回值类型），ElemType（数据元素类型）

二：线性表

1：顺序表：

是指将线性表中的各个元素依次存放在一组地址连续的存储单元中，通常将这种方法存储的线性表称为顺序表。

顺序表逻辑上相邻的元素在物理上也是相邻的。:

2：链表：

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

2.1单链表：

结构：节点中含有一个指针指向下个节点

2.2 循环链表：

结构：单链表中将最后一个节点的指针指向第一个元素的数据域，将其构成循环状态

判断单链表为空的条件是head->next==NULL，而判断循环单链表为空的条件是head->next==head。访问第一个结点即rear->next->next。

 

2.3 双向循环链表：

结构：节点中含有两个指针，分别指向下一个节点和前一个节点

 判断带头结点的双向循环链表为空的条件是：head->prior ==head  || head->next == head。

应用：

单向线性表的合并，其他的类式。

 1 void MergeOrderList_Sq(SqList LA,SqList LB,SqList &LC)
 2 {  //已知顺序有序表LA和LB的元素按值非递减排序
 3     //归并LA和LB得到新的顺序有序表Lc，LC的元素也按值非递减排序
 4     LC.length=LA.length+LB.length;//新表长度为带合并两表的长度之和
 5     LC.elem=new ElemType[LC.length];//为合并后的新表分配一个数组空间
 6     pc=LC.elem;                                    //指针pc指向新表的第一个元素
 7     pa=LA.elem; pb=LB.elem; //指针pa和pb的初值分别指向两个表的第一个元素
 8     pa_last=LA.elem+LA.length-1;//指针pa_last指向LA的最后一个元素
 9     pb_last=LB.elem+LB.length-1;//指针pb_last指向LB的最后一个元素
10     while((pa<pa_last)&&(pb<=pb_last))//LA和LB均为到达表尾
11     {
12           if(*pa<=*pb) *pc++=*pa++;//以此取两表中较小的节点插入到LC的最后
13           else *pc++=*pb++;
14      }
15      while(pa<=pa_last)  *pc++=*pa++;//LB已到达表尾，依次将LA的剩余元素插入LC的最后
16      while(pb<=pb_last)  *pc++=*pb++；//LB已到达表尾，依次将LA的剩余元素插入LC的最后
17 }
18 //链式存储结构
19 void MergeLineList L(LinkList &LA,LinkList &LB,LinkList &LC){
20 {//已知单链表LA和LB的元素按值非递减排序
21       pa=LA->next;pb=LB->next;//pa和pb分别指向两个表的第一个节点
22       LC=LA;//用LA的头节点作为LC的头节点，
23       pc=LC;//pc的初值指向LC的头节点
24       while(pa&&pb)
25       {//LA和LB均未到达表尾，依次取两表中值较小的节点插入到LC的最后
26             if(pa->data<=pb->data)//取pa所指节点
27             {
28                   pc->next=pa;//将pa所指节点链接到pc所指节点之后
29                   pc=pa;//pc指向pa
30                   pa=pa->next;//pa指向下一节点
31               }
32              else//取pb所指节点
33             {
34                  pc->next=pb;
35                  pc=pb;
36                  pb=pb->next;
37               }
38          }
39         pc->next=pa?pa:pb//将非空表剩余段插入到pc所指节点之后
40         delete   LB;//释放LB的头节点
41 }
42          
43   
44    

 

三：栈

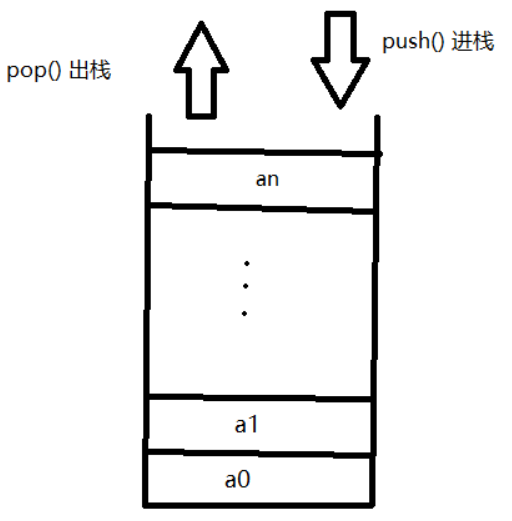
是限制在表一端进行插入和删除操作的线性表。“先进后出”，允许进行插入、删除操作的这一端称为栈顶（Top），另一个固定端称为栈底。

1：顺序栈

利用顺序存储方式实现的栈称为顺序栈。类似于顺序表的定义，栈中的数据元素用一个预设的足够长度的一维数组来实现

2：链栈

用链式存储结构实现的栈称为链栈。通过链栈用单链表表示，因此其结点结构与单链表的结点结构相同，在此用LinkStack表示

 

例1：若栈容量为3，以ABCDE入栈，以下不可能的出栈顺序为（）

例2：表达式的转换

前缀表达式：从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 op 次顶元素），并将结果入栈；重复上述过程 直到表达式最左端，最后运算得出的值即为表达式的结果。

中缀表达式：即为正常的表达式

后缀表达式：从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 op 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式

四：队列

队列也是一种运算受限的线性表，又叫先进先出表

2：循环队列

元素个数=（尾-头+表长）%表长 

入队：rear=（rear+1）%MAX    

队空：rear==front  

对满：（rear+1）%MAX==front

3：链对

五：串

1：顺序存储

串长

法一：

 

 这种存储方式可以直接得到串的长度：s.curlen+1 。

法二：C语言中处理定长串的方法就是这一点，它用“\0”来表示串的结束。这种存储方法不能直接得到串的长度，根据当前字符是否是“\0”来确定串是否结束，从而计算出串的长度。

 

2：堆分配存储

 

例1：KMP算法

六：数组 

1：对称矩阵

压缩存储：若n阶矩阵中的元满足Aij = Aji 则该矩阵可以用一维数组进行压缩存储，

可以以行序为主序存储矩阵下三角（包括对角线）中的元，假设一维数组sa[n(n+1)/2] 存储n阶矩阵，则sa[k]和矩阵元aij之间存在着一一对应的关系:k=大（大-1）/2+小-1；（大与小相对于 i 于 j 相对比而取值）

三角矩阵：

以主对角线划分，三角矩阵有上三角矩阵和下三角矩阵两种。上三角矩阵是指下三角（不含对角线）中的元均为常数 c 或 零 的 n 阶矩阵，下三角矩阵与之相反。对三角矩阵进行压缩存储时，除了和对称矩阵一样，只存储其上（下）三角中的元素之外，再加一个存储常数 c 的存储空间即可

上三角矩阵：

sa[k]和矩阵Aij间的对应关系为  当 i > =j 时，k = i*(i-1)*(2*n-i+2)/2+(j-1) 当 i < j 时，n*(n+1)/2

下三角矩阵：

 sa[k]和矩阵Aij间的对应关系为  当 i >=j 时，i*(i-1)/2 + j -1 当 i <j 时，n*(n+1)/2

三对角矩阵：

      

七：广义表

表头：非空广义表的的第一个元素      表尾：除了表头都叫表尾