几种常见的排序算法
几种常见的排序算法
冒泡排序(Bubble Sort):
冒泡排序是一种计算机科学领域的较简单的排序算法。以数字排序为例,冒泡排序让相连的两个数字进行比较,将比较大的数字放在右边。假设最大的数字N在最左边。第一趟排序的时候,N每次和右边的数字做对比,都将比右边的数字大,然后将N一直往右移动只到最右。情形犹如冒泡,因此称为冒泡排序。
以下为冒泡排序的一次范例:
| 原始数据 | 10 | 1 | 66 | 20 | 19 | 3 |
| 第1次排序 | 1 | 10 | 20 | 19 | 3 | 66 |
| 第2次排序 | 1 | 10 | 19 | 3 | 20 | 66 |
| 第3次排序 | 1 | 10 | 3 | 19 | 20 | 66 |
| 第4次排序 | 1 | 3 | 10 | 19 | 20 | 66 |
| 第5次排序 | 1 | 3 | 10 | 19 | 20 | 66 |
第一趟排序对数组的0、1位置进行排序,10>1,将1放在10之后;10<66,不动;66>20,对换20跟66的位置;66>19;对换66跟19的位置;66>3,对换66跟3的位置。从而获取到了最大值66。
第二趟排序进行跟上面一样的对比,只是66可以不参与比较。获取第二大的数字20
第三趟排序获取第三大的数字19。
。。。。。。
重复步骤,完成数字排序。
以java代码为例,进行编码:
public static void bubbleSorted(Integer[] list) { Integer temp; for (int i = 0; i < list.length; i++) { //如果没有进行数据调换,则说明排序完成 boolean didSwap = false; for (int j = 0; j < list.length - i - 1; j++) { if (list[j] > list[j + 1]) { temp = list[j]; list[j] = list[j + 1]; list[j + 1] = temp; didSwap = true; } } if (didSwap == false) { return; } } }
分析:冒泡排序每一次都进行了N次迭代,因此排序的时间复杂度为O(n²)。它过于简单了,以至于可以毫不费力地写出来。然而当数据量很小的时候它会有些应用的价值,数据量比较小的时候其实也有其他更优的选择,所以一般不会使用冒泡排序。
插入排序(insertion Sort):
插入排序是一种最简单的排序算法,假设待排序的数组长度为N,插入排序必须进行N-1趟排序。插入排序的第M趟排序,保证数组的0位置开始到M位置处于已排序状态。
以下为插入排序的一次范例:
| 原始数据 | 10 | 1 | 66 | 20 | 19 | 3 |
| 第1次排序 | 1 | 10 | 66 | 20 | 19 | 3 |
| 第2次排序 | 1 | 10 | 66 | 20 | 19 | 3 |
| 第3次排序 | 1 | 10 | 20 | 66 | 19 | 3 |
| 第4次排序 | 1 | 10 | 19 | 20 | 66 | 3 |
| 第5次排序 | 1 | 3 | 10 | 19 | 20 | 66 |
第一趟排序对数组的0、1位置进行排序,10>1,将1放在10之后。
第二趟排序对数组的0、1、2位置进行排序,1<10<66,不进行数据移动。
第三趟排序对数组的0、1、2、3位置进行排序,1<10<19<20。移动数据。
。。。。。。
重复上述步骤,直到数组中的所有元素排序完成。
以java代码为例,进行编码:
1 public static void insertionSorted(Integer[] list) { 2 for (int i = 1; i < list.length; i++) { 3 Integer temp = list[i]; 4 int j; 5 for (j = i; j > 0 && list[j - 1] > temp; j--) { 6 list[j] = list[j - 1]; 7 } 8 list[j] = temp; 9 } 10 }
分析:由于插入排序每一次都进行了N次迭代,因此插入排序的时间复杂度为O(n²)。而且在数组的数量比较小的情况下,插入排序的速度是很可观的。插入排序跟冒泡排序经常会拿起来做比较,看下方数据比较:
| 算法名称 | 最差时间复杂度 | 平均时间复杂度 | 最优时间复杂度 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(N²) | O(N²) | O(N) | O(1) | 稳定 |
| 插入排序 | O(N²) | O(N²) | O(N) | O(1) | 稳定 |
两者在数据上的表现非常一致。但是插入排序可能因为循环不成立而退出,从而减少了比较的次数。因此一般情况下,插入排序是相比冒泡排序更优秀的排序算法,小数据量的情况下一般优先选择插入排序。
希尔排序(Shellsort):
希尔排序的名称来自他的发明者DonaldShell,希尔排序是第一批冲破二次时间屏障的算法之一。它的算法思路是通过比较一定距离的元素,逐渐缩减,直到比较距离为1的元素。所以希尔排序也叫缩减增量排序。
以下为希尔排序的一次范例:
| 原始数据 | 10 | 1 | 66 | 20 | 19 | 3 |
| 第1次排序(间距为3) | 10 | 1 | 3 | 20 | 19 | 66 |
| 第2次排序(间距为2) | 3 | 1 | 10 | 20 | 19 | 66 |
| 第3次排序(间距为1) | 1 | 3 | 10 | 19 | 20 | 66 |
第一趟排序间距为3,将10与20比较;1跟19比较;66跟3比较,交换66跟3的位置。
第二趟排序间距为2,将10与3比较,交换10个3的位置;20跟1比较;10跟19比较;66跟20比较;
第三趟排序间距为1,将1跟3比较,交换1跟3的位置;3跟10比较;10跟20比较;20跟19比较,交换19跟20的位置。19再跟10比较;20跟66比较;
以java代码为例,进行编程:
1 public static void shellSorted(Integer[] list) { 2 for (int gap = 3; gap > 0; gap--) { 3 for (int i = gap; i < list.length; i++) { 4 Integer temp = list[i]; 5 int j; 6 for (j = i; j - gap >= 0 && list[j - gap] > temp; j -= gap) { 7 list[j] = list[j - gap]; 8 } 9 list[j] = temp; 10 } 11 } 12 }
分析:上述代码中,gap为3、2、1,称为增量序列。希尔排序的效率依赖于增量序列的选择。希尔排序的问题在于,增量未必是互素的。
Hibbard提出一个增量序列,称为Hibbard增量序列。Hibbard增量序列形如1、3、7、.....、2^k-1。因此增量之间没有公因子,所以Hibbard增量的最坏运行情形时间为O(N^3/2),平均运行时间为O(N^5/4)。
Sedgewick提出的几种增量序列,最坏运行时间为O(N^4/3),平均运行时间为O(N^7/6),其中最好的序列为{1,5,19,41,109....},该序列9*4^i-9*2^i+1,或者4^i-3*2^i+1的形式。
堆排序(Heapsort):
堆排序是一种使用堆为结构来进行排序的算法。利用二叉堆作为优先队列,进行排序,每次获取堆中最大值或者最小值,放入新序列中。实现了队列的排序。
堆排序例子:
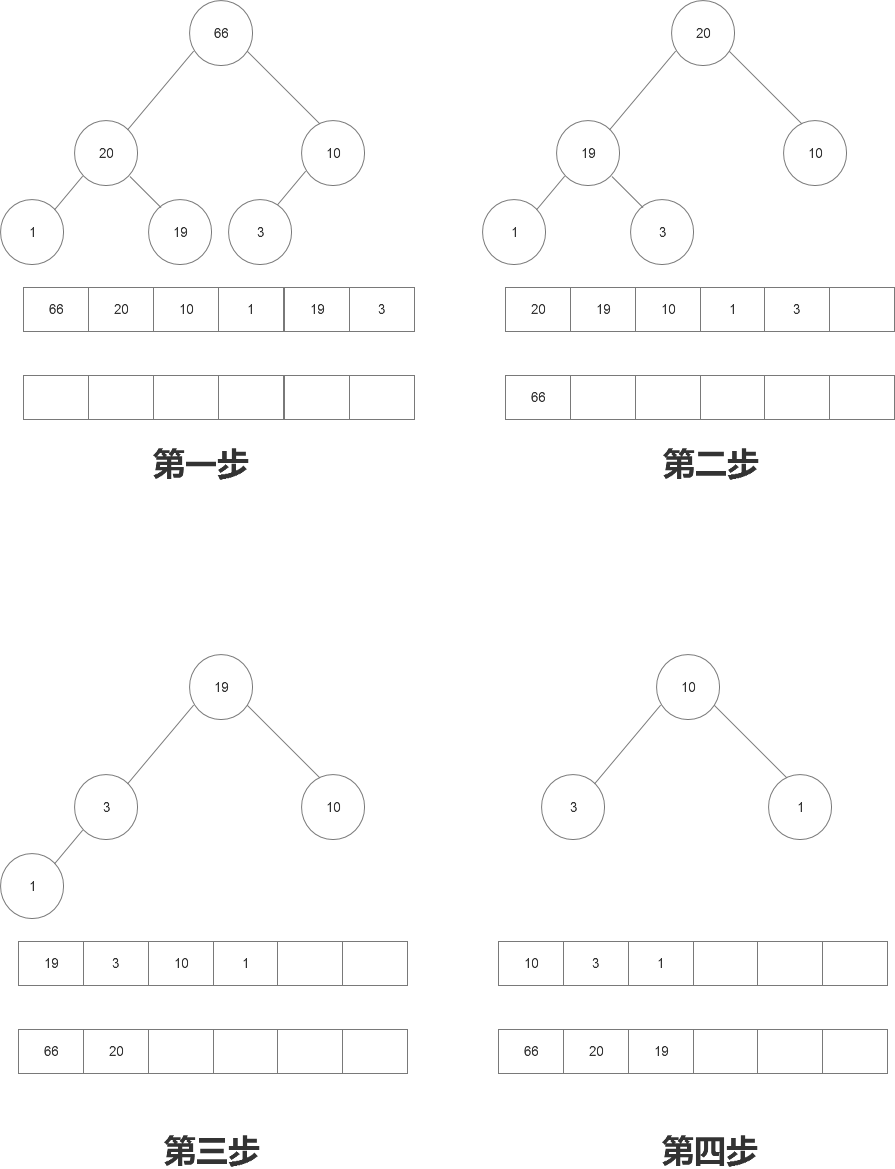
第一步获取最大值66;
第二步获取最大值20;
第三部获取最大值19;
。。。。。
以上述方式获取新的排序队列。
以java代码为例,进行编程:
1 private static int leftChild(int i) { 2 return 2 * i + 1; 3 } 4 5 private static void perDown(Integer[] list, int i, int n) { 6 int child; 7 Integer temp; 8 for (temp = list[i]; leftChild(i) < n; i = child) { 9 child = leftChild(i); 10 if (child != n - 1 && list[child] < list[child + 1]) { 11 child++; 12 } 13 if (temp < list[child]) { 14 list[i] = list[child]; 15 } else { 16 break; 17 } 18 } 19 list[i] = temp; 20 } 21 22 public static void heapSort(Integer[] list) { 23 Integer temp; 24 25 for (int i = list.length / 2 - 1; i >= 0; i--) { 26 perDown(list, i, list.length); 27 } 28 for (int i = list.length - 1; i > 0; i--) { 29 temp = list[0]; 30 list[0] = list[i]; 31 list[i] = temp; 32 perDown(list, 0, i); 33 } 34 }
分析:堆排序种,第一阶段构建堆最多用到2N次比较,第二阶段,第i次deleteMax最多用到2Logi次比较,总共最多2N*LogN-O(N)次比较。堆排序也是一个非常稳定的算法。他的比较平均只比最坏情况指出的情况略少。
归并排序(mergeSort):
归并排序的用法于上面几种排序不同,归并排序使用场景是存在已经排序完成的队列A和队列B,现要将已经排序完成A、B两个队列合并成队列C;归并排序以O(N*logN)的最坏情形时间运行,而使用的比较时间几乎是最优的。它是递归算法的一个好的事例应用。
归并排序例子:
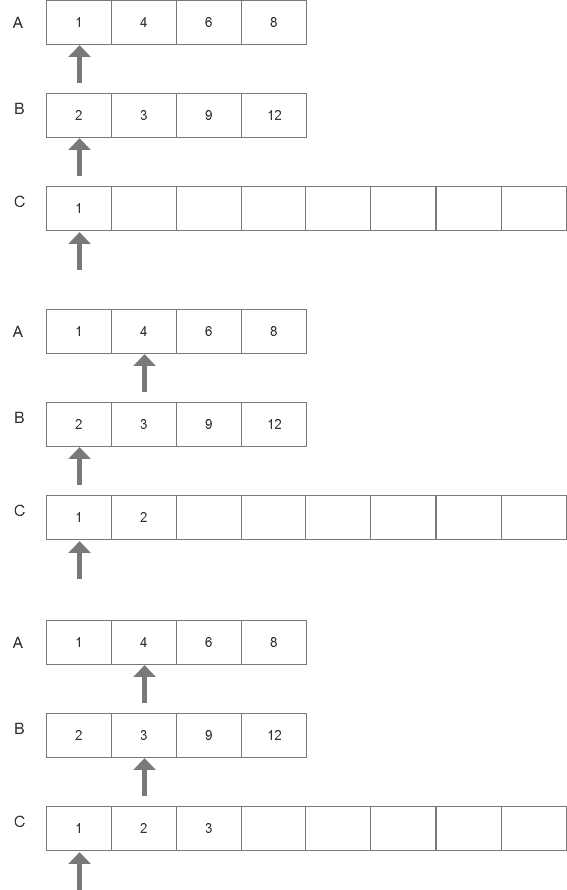
A、B为已经排序的数组,C为新建数组。A、B数组一开始有个指针指向第一个元素。
第一步,比较A、B第一个元素1<2。将1写入C中,A的指针往右移动。
第二部,比较2<4,将2写入C中,B的指针往右移动。
.....
同上,A或者B全部写入后,将另外的数组剩余的数字也写入C中。
在单个数组进行排序的时候使用归并排序,则是将单个数组拆分成两个数组,将这两个数组分别排序完成后,再进行归并。
以java代码为例,进行编程:
1 public static void mergeSort(Integer[] list) { 2 Integer[] tempArray = new Integer[list.length]; 3 mergeSort(list, tempArray, 0, list.length - 1); 4 } 5 6 private static void mergeSort(Integer[] list, Integer[] tempArray, int left, int right) { 7 if (left >= right) { 8 return; 9 } 10 int center = (left + right) / 2; 11 mergeSort(list, tempArray, left, center); 12 mergeSort(list, tempArray, center + 1, right); 13 merge(list, tempArray, left, center + 1, right); 14 } 15 16 private static void merge(Integer[] list, Integer[] tempArray, int leftPos, int rightPos, int rightEnd) { 17 int leftEnd = rightPos - 1; 18 int tempPos = leftPos; 19 int numberElements = rightEnd - leftPos + 1; 20 21 while (leftPos <= leftEnd && rightPos <= rightEnd) { 22 if (list[leftPos] <= list[rightPos]) { 23 tempArray[tempPos++] = list[leftPos++]; 24 } else { 25 tempArray[tempPos++] = list[rightPos++]; 26 } 27 } 28 29 while (leftPos <= leftEnd) { 30 tempArray[tempPos++] = list[leftPos++]; 31 } 32 33 while (rightPos <= rightEnd) { 34 tempArray[tempPos++] = list[rightPos++]; 35 } 36 37 for (int i = 0; i < numberElements; i++, rightEnd--) { 38 list[rightEnd] = tempArray[rightEnd]; 39 } 40 }
分析:归并排序的运行时间为O(N*logN),但是归并排序需要线性附加内存。整个算法在花费了数据拷贝再拷回来这些附加工作,减慢了排序速度。这种拷贝可以通过list和tempArray进行角色交换来避免。在java中归并排序的数据移动是很省时的,因为归并排序只是移动了对象的引用。在java类库中泛型排序使用的就是归并算法。
快速排序(mergeSort):
快速排序是实践中的一种快速排序算法,在Java中对基本类型的排序特别有用,也是面试时候最容易被问道的排序算法。快排的平均运行时间为O(N*logN),最坏情形为O(N^2),但是经过稍许努力就能让最坏情况很难出现。通过快排和堆排序进行结合,由于堆排序的最坏为O(N*logN),我们可以对几乎所有的输入都能达到快速排序的快速运行时间。
快排例子:
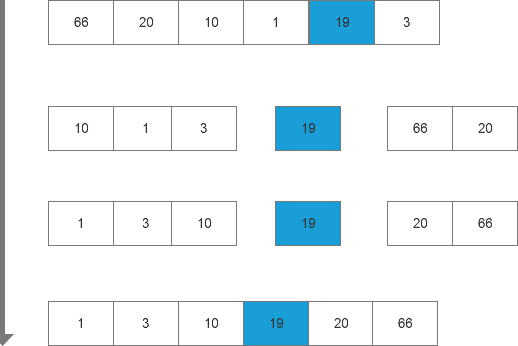
第一步,随机获取枢纽元,上例中为19。
第二步,将其他数字跟19做比较,一组比19小,一组等于19,一组大于19。
第三步,将大于19和小于19的两组进行排序。
第四步,按照顺序将他们写入数组中。
以java代码为例,进行编程:
1 public static void quickSort(Integer[] list) { 2 quickSort(list, 0, list.length - 1); 3 } 4 5 private static void quickSort(Integer[] list, int left, int right) { 6 if (left + CUTOFF <= right) { 7 Integer pivot = media3(list, left, right); 8 int i = left + 1, j = right - 2; 9 while (true) { 10 //=pivot,防止list[i]=list[j]=pivot,进入死循环 11 while (i<list.length-1&&list[i] <=pivot) { 12 i++; 13 } 14 while (j>0&&list[j] >= pivot) { 15 j--; 16 } 17 if (i < j) { 18 swapReferences(list, i, j); 19 }else { 20 break; 21 } 22 } 23 //分组完成再把中值拎回来放在中间 24 swapReferences(list, i, right - 1); 25 26 //防止数组中数字一样进入死循环 27 if(left<i-1&&i-1<right){ 28 quickSort(list, left, i - 1); 29 } 30 if(left<i+1&&i+1<right){ 31 quickSort(list, i + 1, right); 32 } 33 } else { 34 insertionSorted(list, left, right); 35 } 36 } 37 38 private static Integer media3(Integer[] list, int left, int right) { 39 int center = (left + right) / 2; 40 if (list[center] < list[left]) { 41 swapReferences(list, left, center); 42 } 43 if (list[right] < list[left]) { 44 swapReferences(list, left, right); 45 } 46 if (list[right] < list[center]) { 47 swapReferences(list, center, right); 48 } 49 //先把中值拎出去,方便交换操作 50 swapReferences(list, center, right - 1); 51 return list[right - 1]; 52 } 53 54 private static void swapReferences(Integer[] list, int i, int j) { 55 Integer temp = list[i]; 56 list[i] = list[j]; 57 list[j] = temp; 58 }
分析:枢纽元的选择对快排的效率有很大影响,随机选取枢纽元是很比较靠谱的做法。比较不好的选取方式选取第一个或者最后一个,上述代码的枢纽元用的三数中值分割法,取数组第一位,中间位,和最后一位,从三个数中去中间值作为枢纽元。因为快排是递归的分隔数组进行排序,当数组被切割得比较小的时候(N<=20),可以使用插入排序来完成,效率会更高。快速排序的最坏情况为O(N^2),最好情况为O(NlogN),平均情况也是O(NlogN)。
桶排序(bucketSorted):
当输入的数据由仅小于M的正整数来组成,可以使用桶排序来完成。假设有一个存在一个整数数组,数组中的元素不超过10。对这个数组进行排序,创建一个长度为11的数组count,count中的每个元素都为0,当读入数据为i的时候,count(i)加上1,等全部读取完毕之后根据count数将数组排列出来。
桶排序例子:

原数组进行迭代,读到的数据在在count数组中对应下标的地方进行+1操作。等原数组迭代完成后,将count数组读出就是排序完成的数组。
java代码如下:
1 public static void bucketSorted(Integer[] list) { 2 Integer[] count = new Integer[10]; 3 for (int i = 0; i < count.length; i++) { 4 count[i] = 0; 5 } 6 7 for (Integer value : list) { 8 count[value] += 1; 9 } 10 int i = 0; 11 for (int k = 0; k < count.length - 1; k++) { 12 for (int j = 1; j <= count[k]; j++) { 13 list[i++] = k; 14 } 15 } 16 }
分析:桶排序比较简单,然而在业务中很少有机会能使用到。当你的数字M上限比较高的时候,可以使用基数排序来实现。算法的用时为O(M+N),M为桶的个数。如果M为O(N),则总时间为O(N)。
基数排序(radix sort):
基数排序又叫做卡片排序,假设我们有大小在0~999之间数据进行排序,如果使用桶排序就不大合适。此时我们就可以使用基数排序,按照个位、十位、百位数进行三次排序。
基数排序例子:

第一步,根据个位数排序,排序完成依次读取。
第二部,根据十位数排序,排序完成依次读取。
第三部,根据百位数排序,排序完成依次读取。
由于每一次排序的过程都保留了上一次排序的顺序,所以最后数字能按照大小进行排序。
以java代码为例,进行编程:
1 public static void radixSort(Integer[] list, int numberLen) { 2 3 //初始化 4 final int BUCKETS = 10; 5 ArrayList<Integer>[] buckets = new ArrayList[BUCKETS]; 6 for (int i = 0; i < BUCKETS; i++) { 7 buckets[i] = new ArrayList<Integer>(); 8 } 9 10 //排序 11 for (int i = 0; i < numberLen; i++) { 12 13 for (Integer num : list) { 14 buckets[(int) ((num / Math.pow(10, i)) % 10)].add(num); 15 } 16 17 int j = 0; 18 for (ArrayList<Integer> bucket : buckets) { 19 for (Integer number : bucket) { 20 list[j++] = number; 21 } 22 bucket.clear(); 23 } 24 } 25 }
分析:基数排序的运行时间为O(p(N+b)),p是排序的趟数,对应上述代码的numberLen。b为桶的个数,对应上述代码中的BUCKETS。桶排序和基数排序实现了线性时间完成排序。但是桶排序和基数排序的条件相比其他排序苛刻。
计数基数排序(counting radix sort):
计数基数排序是基数排序的另外一个实现,他避免使用ArrayList,取而代之的是用一个计数器。当数组扫描的对应的数字的时候,计数器在对应的位置上+1。等所有排序完成之后,根据计算器的数据,将对应的数据翻出来。完成排序。

第一步,遍历原数组,读取到值之后,在对应的计数器上+1,比如读取到5,则在计数器的5上加1。
第二部,将计数器上数据进行叠加,获取对应数字的位置,计数器上1的位置上为0的数量+1的数量,2位置上的数量为0的数量+1的数量+2的数量。
第三部,根据计数器,重排排序数组。
以java代码为例,进行编程:
1 public static Integer[] countingSort(Integer[] list) { 2 Integer max = getMax(list); 3 4 Integer min = getMin(list); 5 6 Integer[] result = new Integer[list.length]; 7 8 int k = max - min + 1; 9 int[] count = new int[k]; 10 for (int i = 0; i < list.length; ++i) { 11 count[list[i] - min] += 1; 12 } 13 for (int i = 1; i < count.length; ++i) { 14 count[i] = count[i] + count[i - 1]; 15 } 16 for (int i = list.length - 1; i >= 0; --i) { 17 result[--count[list[i] - min]] = list[i];//按存取的方式取出c的元素 18 } 19 return result; 20 } 21 22 private static Integer getMax(Integer[] list) { 23 int b[] = new int[list.length]; 24 int max = list[0]; 25 for (int i : list) { 26 if (i > max) { 27 max = i; 28 } 29 } 30 return max; 31 } 32 33 private static Integer getMin(Integer[] list) { 34 int b[] = new int[list.length]; 35 int min = list[0]; 36 for (int i : list) { 37 if (i < min) { 38 min = i; 39 } 40 } 41 return min; 42 }
分析:计数排序也可以用来做字符串的排序。但是和桶排序有一个共同的问题是,当要进行排序的数字之间跨度非常大,或者字符串排序中字符串的长度特别长的时候,该算法的优势就没有那么明显,甚至完全消失。
外部排序(external sorting):
以上的各种算法,都是将要排序的数组放到内存之中进行排序,但是在一些特殊场景下,需要被排序的内容数量太大,而没办法装载入内存的时候,我们就需要用到外部排序算法。下面简单介绍一种在磁盘上进行外部排序的算法,因为在磁带上访问一个元素需要把磁带转到正确的位置上,因此磁带需要被连续访问才能提高效率。我们通过部分排序的方式,在磁带上顺序得读入数据和写出数据来完成排序。假设现在我们有4个磁带,a1,a2,b1,b2,内存一次可以容纳3个数据,见下方模型:

1、一开始数据并无排序,因为内存每次可以读入3个数据,每三个数据进行一次排序,保存12个数据中,有四队有序数据,b1两组,b2有两组。
2、使用归并排序的套路,磁盘的磁头分别指向两组数据的开头部分,读入后进行比较,然后按顺序写入a1中。第三组数据和第四组数据写入a2中。
3、跟上述方式一样,磁头指向a1、a2的开始部分,然后将比较后的的数据写入b1中。
排序完成。
分析:上方的模型比较简单,当我们有更多磁带,就可以进行多路合并,即同时比较多组数据来减少数据写入写出的次数。但是通过增加磁带来减少读写次数并不方便,还可以通过多相合并,即通过分配不同磁带的不同顺串的数量来完成上述工作。
总结:排序是最古老,被研究得最完备的问题之一。对于大部分内部排序的应用,不是插入、希尔、归并、就是快排。就主要取决于输入数量的大小和底层环境决定的。插入排序适用于非常少量的输入。中等规模用希尔是个不错的选择,只要增量序列合适,就能表现优异。归并排序最坏情况为O(NLogN),但是却需要额外的空间,但是比较的次数几乎是最优的。快排并不保证提供最坏的时间复杂度,并且编程麻烦。但是几乎可以肯定做到O(N logN),配合堆排序,就可以保证最坏情况为O(N logN)。基数排序可以在线性时间内排序,在特定环境下是相对比较的排序法更加实用。而外部排序则处理数据量大无法完全放入内存的情况。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号