找最大子矩阵

1.题目。

题目:返回一个整数数组中最大子数组的和。
要求：
输入一个整形数组，数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。

程序要使用的数组放在一个叫 input.txt 的文件中,  文件格式是:
数组的行数,
数组的列数,
每一行的元素,  (用逗号分开)

2.设计思想。

先将intput.txt中的矩阵写入二维数组s[][]中，实现每相邻两行相加，相邻三行相加，一直到所有行相加，然后再求没个一维数组的最大子矩阵。

3.代码。

#include<iostream.h>
#include<fstream.h>
#define MAX 1000
#define Max 1000
int qiuzuidazishuzu(char a[],int k) //k为列数；
{
    int m=0,b[MAX],n=0;
    for(int l=1;l<k+1;l++)
    {
        for(int i=0;i<2*k-(2*l-1);i=i+2)
        {
            for(int j=i;j<i+2*l-1;j=j+2)
            {
                
                if(j>2*k-1)
                {
                    break;
                }
                else
                    m=m+a[j]-48;
            }
            b[n]=m;
            m=0;
            n=n+1;
        }
    }
    int  max=b[0];
    for(int i=1;i<n;i++)
    {
        if(max<b[i])
            max=b[i];
    }
    
    return max;
}


int main()
{
    int h,l,a[100],n=0,p=0;
    int e[100]={0};

    char s[100][100];
    char r,t;
    ifstream inFile("intput.txt",ios::in);
    inFile>>h>>r>>l>>t;
    for(int i=0;i<h;i++)
    {
        inFile>>s[i];
        
    }
    for(i=0;i<h;i++)
    {
        cout<<s[i]<<endl;
        
    }
    for(i=0;i<3;i++)
    {
        a[i]=qiuzuidazishuzu(s[i],l);
    }
    for(i=0;i<2;i++)
    {
        for(int j=0;j<5;j=j+2)
        {
            s[i][j]=s[i+1][j]+s[i][j]-48;
        }
    }
    for(i=0;i<2;i++)
    {
      a[i+3]=qiuzuidazishuzu(s[i],l);
    }
    for(int j=0;j<5;j=j+2)
        s[0][j]=s[0][j]+s[2][j]-48;
    for(i=0;i<1;i++)
    {
      a[i+5]=qiuzuidazishuzu(s[i],l);
    }
    
    for(i=0;i<10;i++)
    {
        if(a[0]<a[i])
            a[0]=a[i];
    }
    cout<<"最大子矩阵的值为:";
    cout<<a[0]<<endl;;
    return 0;
}

4.实验截图。

 

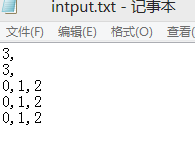
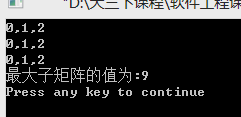
5.体会。

多个人结组编写程序，可以提出更多意见，使程序更完善。