相似度度量计算
看到很多地方在用这个, 就 总结一下:
相似度度量(Similarity),即计算个体间的相似程度,相似度度量的值越小,说明个体间相似度越小,相似度的值越大说明个体差异越大。
对于多个不同的文本或者短文本对话消息要来计算他们之间的相似度如何,一个好的做法就是将这些文本中词语,映射到向量空间,形成文本中文字和向量数据的映射关系,通过计算几个或者多个不同的向量的差异的大小,来计算文本的相似度。下面介绍一个详细成熟的向量空间余弦相似度方法计算相似度
1.夹角余弦计算相似度度量
弦相似度也将特定目标,即物品或者用户作为坐标上的点,但不是坐标原点。基于此与特定的被计算目标进行夹角计算。具体如图5-3所示:
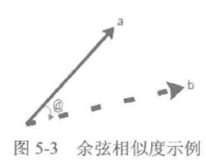
从图5-3可以很明显地看出,两条射线分别从坐标原点触发,引出一定的角度。如果两个目标较为相似,则其射线形成的夹角较小。如果两个用户不相近,则两条射线形成的夹角较大。因此在使用余弦度量的相似度计算中,可以用夹角的大小来反映目标之间的相似性。
公式
余弦相似度的计算公式如下所示。
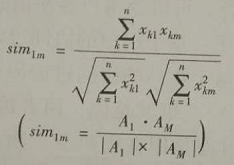
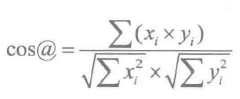
例如: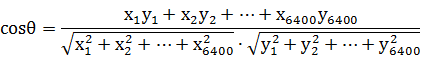
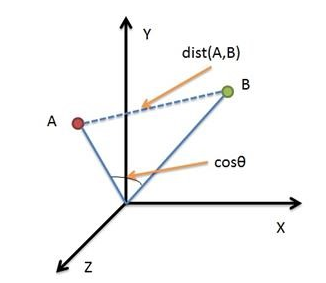
从公式可以看到,余弦值的大小在[-1,1]之间,值的大小与夹角的大小成正比。
计算过程:
在非直角三角形中,余弦定理的公式是
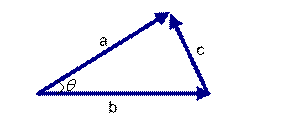
图(5)
三角形中边a和b的夹角 的余弦计算公式为:
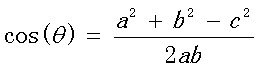
公式(2)
在向量表示的三角形中,假设a向量是(x1, y1),b向量是(x2, y2),那么可以将余弦定理改写成下面的形式:
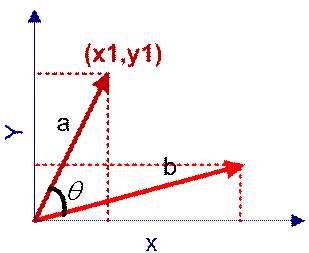
向量a和向量b的夹角 的余弦计算如下:
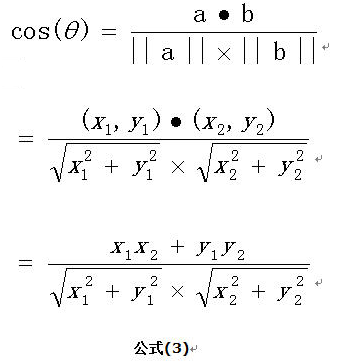
扩展,如果向量a和b不是二维而是n维,上述余弦的计算法仍然正确。假定a和b是两个n维向量,a是 ,b是 ,则a与b的夹角 的余弦等于:
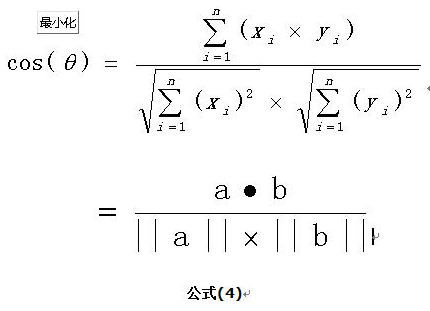
余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似,夹角等于0,即两个向量相等,这就叫"余弦相似性"。
放在一起,一块说一下:
表 相似度计算公式:
|
方法 |
公式 |
说明 |
|
夹角余弦 |
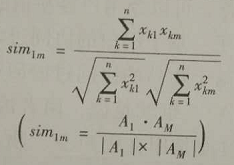
|
取值范围为[-1,1],当余弦值接近±1,表明两个向量有较强的相似性。当余弦值为0时,表示不相关 |
|
杰卡德相似系数 |
def Jaccard(a,b): #仅对0-1矩阵有效 return 1.0*(a*b).sum()/(a+b-a*b).sum() |
分母A1UAm表示喜欢物品1与喜欢物品M的用户总数,分子A1n∩Aw表示同时喜欢物品1和物品M的用户数 |
|
相关系数 |
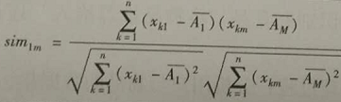
|
相关系数的取值范围[-1,1]。 相关系数的绝对值越大,则表明两者相关度越高 |
|
欧几里得距离(Euclidean dustance) |
相似度值=1/(d+1) 由于在欧几里得相似度计算中,最终数值的大小与相似度成反比,因此在实际应用中常常使用欧几里得距离的倒数作为相似度值,即1/d+1作为近似值。 d,越大,相似度越小。反之成立。
|
欧儿里得相似度计算是一种基于用户之间直线距离的计算方式。在相似度计算中,不同的物品或者用户可以将其定义为不同的坐标点,而特定目标定位为坐标原点。 |
参考:http://blog.csdn.net/u012160689/article/details/15341303
参考:很多网络中的大牛作者没有记录下来,谢你们的无私分享!


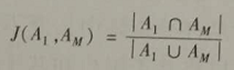
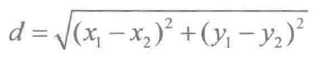

 浙公网安备 33010602011771号
浙公网安备 33010602011771号