贝叶斯学习及共轭先验
共轭先验 是啥？
网上找几篇文章，收集与此！
今天的主要任务是来理解共轭先验以及贝叶斯学习。最近在研究主题模型，里面用到了一些，另外在机器学习中，贝叶斯学习是重要的一个方向，所以有必要学习和掌握。
Contents
1.共轭先验分布
2. 贝叶斯学习
3. Beta分布及共轭先验
1.共轭先验分布
什么又是共轭呢？轭的意思是束缚、控制，共轭从字面上理解，则是共同约束，或互相约束。
在贝叶斯概率理论中，如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律，那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布
比如，某观测数据服从概率分布P(θ)时，当观测到新的X数据时，我们一般会遇到如下问题：
可否根据新观测数据X，更新参数θ？
根据新观测数据可以在多大程度上改变参数θ，即
当重新估计θ的时候，给出新参数值θ的新概率分布，即P(θ|x)
事实上，根据根据贝叶斯公式可知：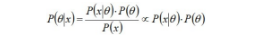
其中，P(x|θ)表示以预估θ为参数的x概率分布，可以直接求得，P(θ)是已有原始的θ概率分布。
所以，如果我们选取P(x|θ)的共轭先验作为P(θ)的分布，那么P(x|θ)乘以P(θ)，然后归一化的结果P(θ|x)跟和P(θ)的形式一样。
换句话说，先验分布是P(θ)，后验分布是P(θ|x)，
先验分布跟后验分布同属于一个分布族，故称该分布族是θ的共轭先验分布（族）。
举个例子。投掷一个非均匀硬币，可以使用参数为θ的伯努利模型，θ为硬币为正面的概率，那么结果x的分布形式为：
其共轭先验为beta分布，具有两个参数α和β，称为超参数（hyperparameters）。且这两个参数决定了θ参数，其Beta分布形式为
然后计算后验概率
归一化这个等式后会得到另一个Beta分布，从而证明了Beta分布确实是伯努利分布的共轭先验分布。
2. 贝叶斯学习
首先，我从最简单的硬币投掷开始。现在给你一个硬币，假设有的概率为正面朝上，那么有
的概率是背
面朝上，那么如果在5次投掷过程中，有3次是正面朝上，那么这个最可能是多少呢？
凭着直观感觉，我们可能会认为是3/5，当然这是根据统计规律得到的结论。那么实际上这是一个二项分布，即
重复n次的伯努利实验。由上述所述，很容易知道其概率表示如下
我们需要这个概率尽量大，那么最终解得的值为3/5。函数图像如下
但是，我们想象一下，如果在5次投掷过程中，5次都正面朝上，那岂不是得到的估计值是1？ 很明显这种情
况得到的估计值不合理。为了避免这种“黑天鹅事件”的发生，需要将值降低一些才能看似更符合常理，那么
我们只需要乘上另一个小于1的概率值就可以达到了。到了这里贝叶斯公式横空出世！如下
其中叫做先验概率，
叫做似然概率，先验概率是对似然概率的一种补充，如上述的掷硬币。而
后验概率正比于似然概率和先验概率的乘积。
3. Beta分布及共轭先验
还是以掷硬币为例，我们已经知道了后验概率正比于似然概率和先验概率的乘积。那么在掷硬币实验中，硬币的
朝向服从伯努利分布，在一系列投掷过程中，假设有次正面朝上，有
次背面朝上，那么似然概率为
现在已经得到了似然概率的形式了，那么如何确定先验概率呢？从理论上来说，任何一个在区间[0, 1]上的分
布函数都符合条件，但是为了更方便地简化计算，最理想的情况就是让先验分布和似然分布有相同的形式，即
如果先验分布是这样的形式，那么计算先验概率和似然概率的乘积就很方便了，只需要将指数相加即可。幸运
的是，有一个很常见的分布恰好满足这个条件，它就是Beta分布。如下
其中是Gamma函数。现在根据先验概率、似然概率和贝叶斯公式来推导后验概率。推导过程如下
在上述中，先验概率叫做似然概率的共轭先验。所谓共轭就是指这两个概率分布具有相同的形式。
最后推荐一些好文章！
参考：
http://blog.csdn.net/acdreamers/article/details/45026459
http://www.360doc.com/content/16/0428/10/478627_554452907.shtml
