BZOJ2151/洛谷P1792 题解
若想要深入学习反悔贪心，传送门。
Description:
有 \(n\) 个位置，每个位置有一个价值。有 \(m\) 个树苗，将这些树苗种在这些位置上，相邻位置不能都种。求可以得到的最大值或无解信息。
Method：
先判断无解的情况，我们显然可以发现，若 \(n<\frac{2}{m}\) ，则是不能在合法的条件下种上 \(m\) 棵树的，故按题意输出Error!即可。
假如有解的话，我们可以很轻松的推出贪心策略：在合法的情况下选择最大的价值。
显然上面的策略是错误的，我们选择了最大价值的点，相邻的两个点就不能选，而选择相邻两个点得到的价值可能更大。
考虑如何设计反悔策略。
我们同样用差值来达到反悔的目的。假设有 \(A\) ，\(B\) ，\(C\) ，\(D\) 四个相邻的点（如图）。
\(A\) 点的价值为 \(a\) ，其他点同理。若：
则：
假如我们先选了 \(B\) 点，我们就不能选 \(A\) 和 \(C\) 两点，这显然是不对的，但我们可以新建一个节点 \(P\) , \(P\) 点的价值为 \(a+c-b\) ，再删去 \(B\) 点。（如图，红色的是删去的点，橙色的新建的点）
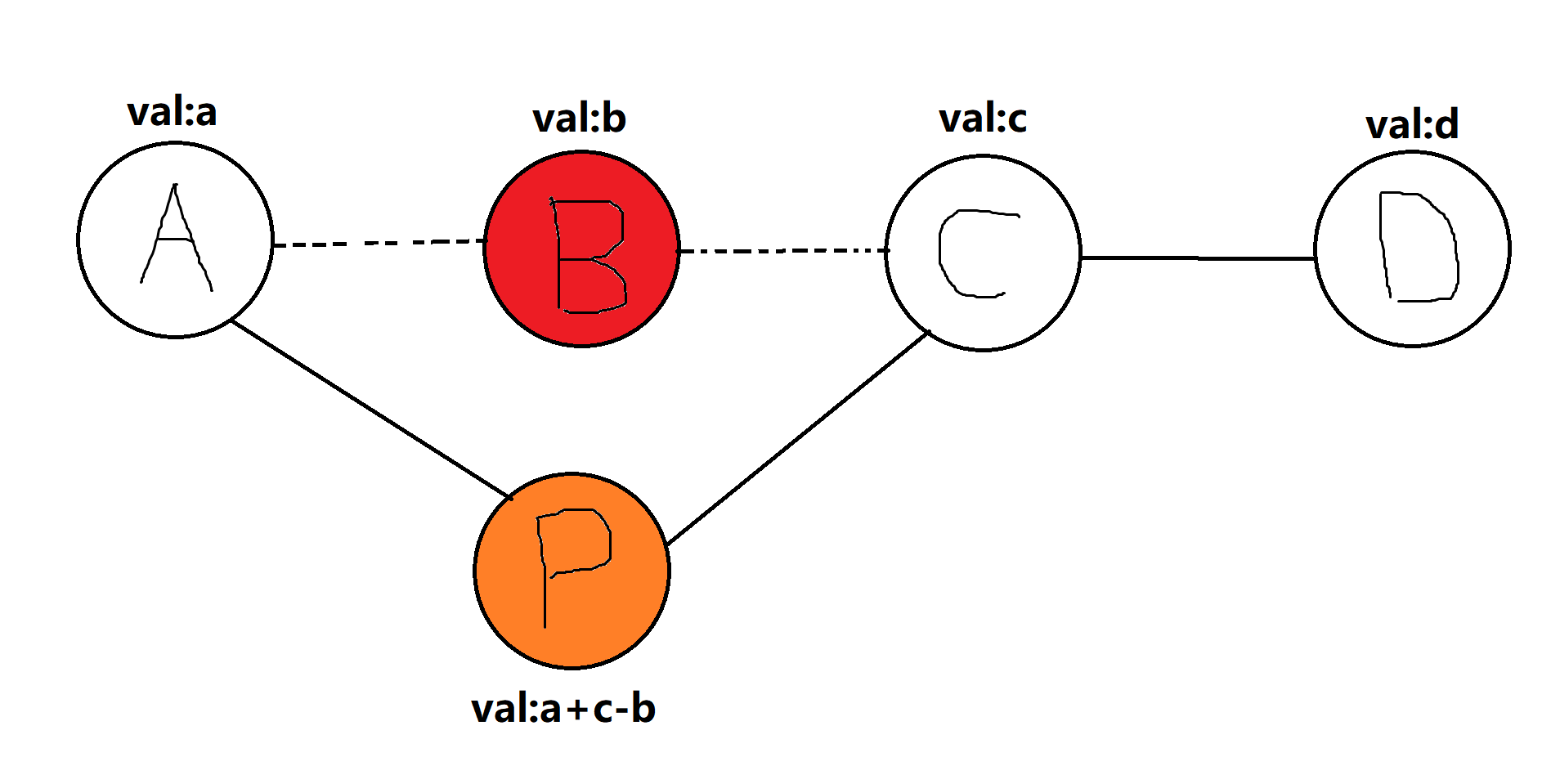
下一次选择的点是 \(P\) 的话，说明我们反悔了（即相当于 \(B\) 点没有选），可以保证最后的贪心最优解是全局最优解。
如何快速插入 \(P\) 点和找出是否选择 \(P\) 点呢？我们可以使用双向链表和小根堆，使得最终在 \(O(n\log n)\) 的时间复杂度下快速求出全局最优解。
Code:
#include<bits/stdc++.h>
#define int long long
#define Maxn 2000010
using namespace std;
inline void read(int &x)
{
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,m;
int w[Maxn],lft[Maxn],rgh[Maxn];
struct node
{
int val,id;
bool operator <(const node &n) const
{
return val<n.val;
}
};
priority_queue<node>qu;
int ind,ans=0;
int vis[Maxn];
signed main()
{
read(n),read(m);
ind=n;
if(n/2<m)
{
puts("Error!");
return 0;
}
for(int i=1;i<=n;i++)
{
read(w[i]);
node tmp;
tmp.id=i;
tmp.val=w[i];
qu.push(tmp);
if(i==1)
{
lft[i]=n;
rgh[i]=i+1;
}else if(i==n)
{
lft[i]=i-1;
rgh[i]=1;
}else
{
lft[i]=i-1;
rgh[i]=i+1;
}
}
for(int i=1;i<=m;i++)
{
while(vis[qu.top().id]) qu.pop();
int id=qu.top().id;
int val=qu.top().val;
qu.pop();
ans+=val;
ind++;
vis[lft[id]]=vis[rgh[id]]=1;
lft[rgh[rgh[id]]]=ind;rgh[lft[lft[id]]]=ind;
lft[ind]=lft[lft[id]];rgh[ind]=rgh[rgh[id]];
w[ind]=w[lft[id]]+w[rgh[id]]-val;
int newid=ind;
int newval=w[ind];
node tmp;
tmp.id=newid;
tmp.val=newval;
qu.push(tmp);
}
printf("%lld\n",ans);
return 0;
}
Warning:
-
一定要记录这个点选没有选过，假如已经选过了，就从堆中丢出去；
-
1与 \(n\) 是相邻的，一定要特判一下；
-
双向链表一定不要写挂了；
-
一定要先将新建的点的价值存入一开始的价值数组，再丢进堆里；（卡在45卡了好久）
-
index是关键字，一定不要使用。（我成功CE了一次）
