吴恩达机器学习课程笔记4-神经网络和反向传播
8 神经网络基础
- 思考: 对训练数据的全拟合方法是使用拉格朗日思想即使用简单的多项式的组合进行完全拟合,神经网络就是在全拟合的基础上进行建立模型,模型可以舍弃一些拟合项,这就是神经网络的数学基础。
- 当特征很多的时候,就不能使用全2次项进行拟合数据,需要考虑交叉乘积项。
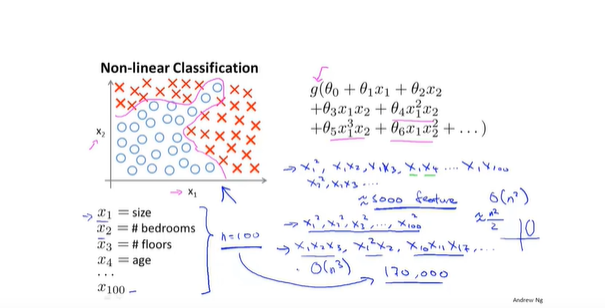
- 视觉特征过多的例子
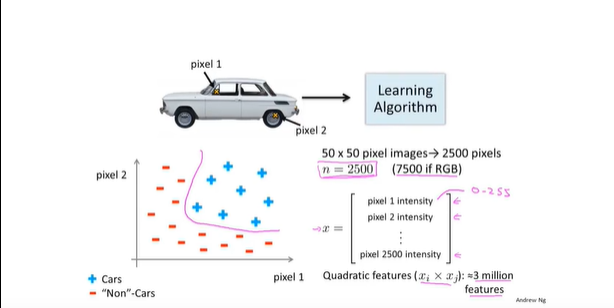
- 基于大脑从数学基础中抽象出神经元
- 当前计算机足以进行运算

- 大脑的一种处理算法值得思考
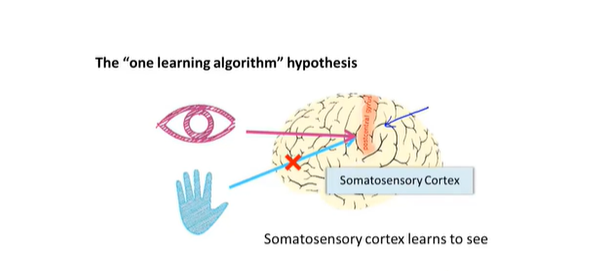
- 从大脑获得启发,从数学基础中获得启发,建立新的神经网络模型
- 如何表示神经网络
- 神经元
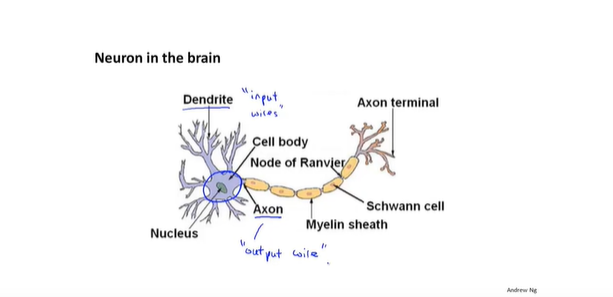
- 神经网络中的神经元
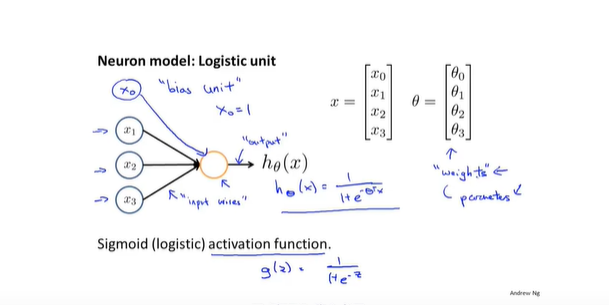
- 实际代码中-> 画出详细神经元的模型图(代码使用)和便于理解的结构图(论文使用)
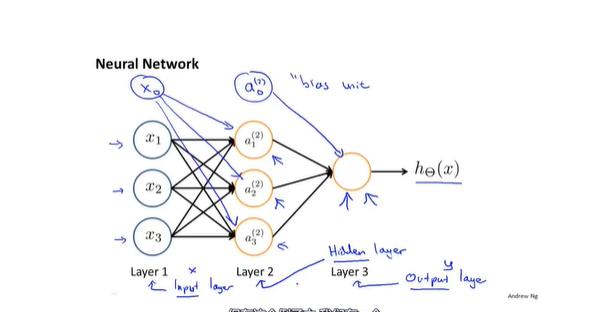
- 记号
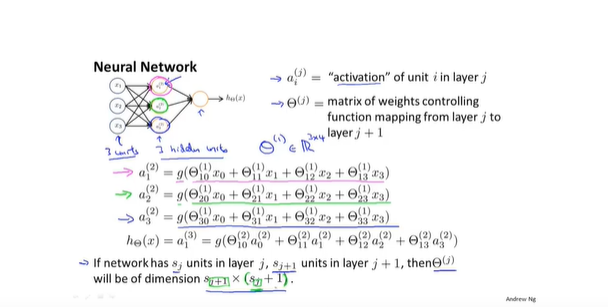
- 向量化实现神经网络
- 向前传播: 从神经网络的数学计算方向定义
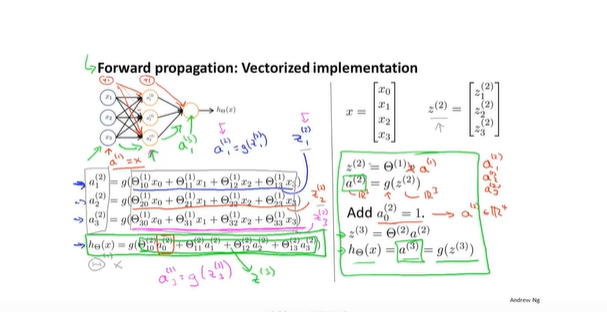
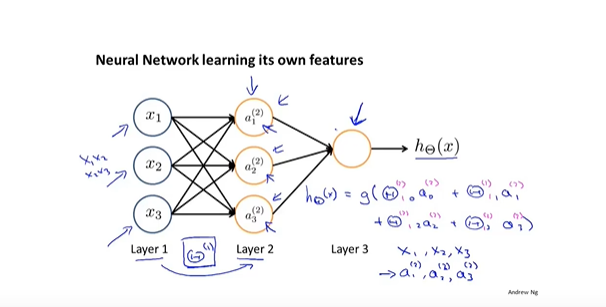
- 模型结构图
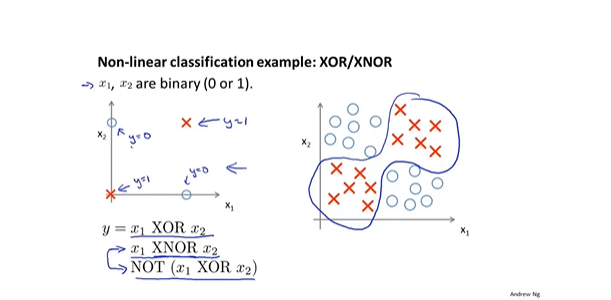
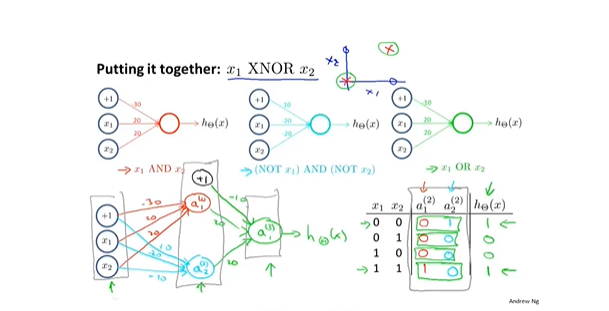
- 神经网络实例 建立XNor异或逻辑神经网络
- XNor逻辑模型
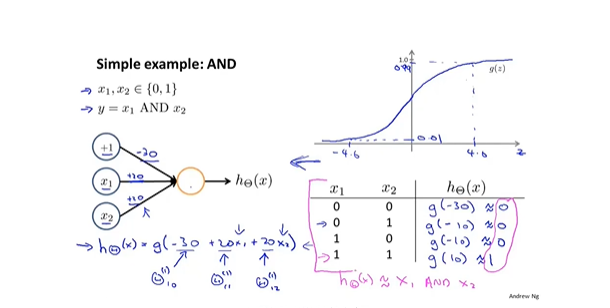
- 真值表看神经网络输出结果
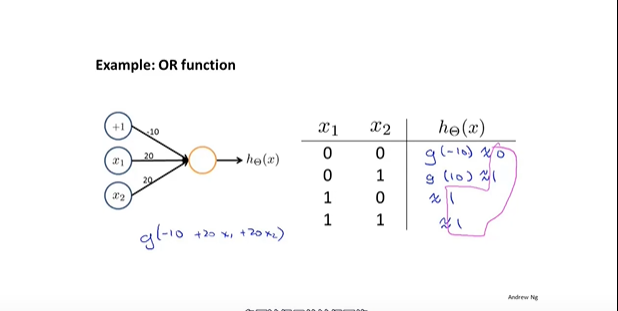
- Or或逻辑模型
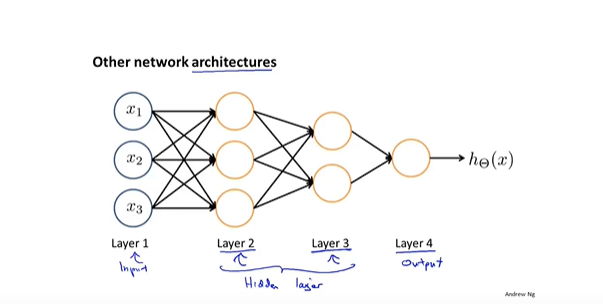
- 神经网络实例2 组合逻辑
- 从隐藏层可以看出,隐藏层可以学习到一些输入数据的深层次特征,从逻辑关系方面说明了神经网络的工作原理。
- LeNet

- 多元分类
- 使用向量作为输出
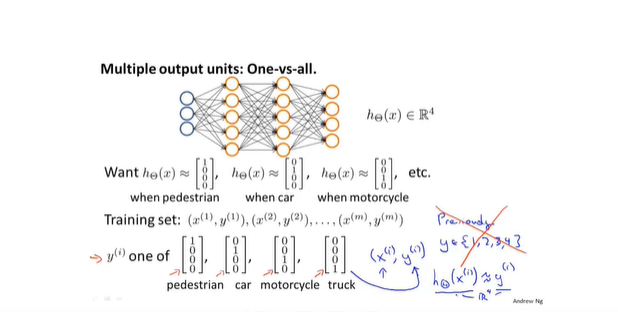
9. 如何使用神经网络模型:损失函数和反向传播
- 损失函数,具有K维输出
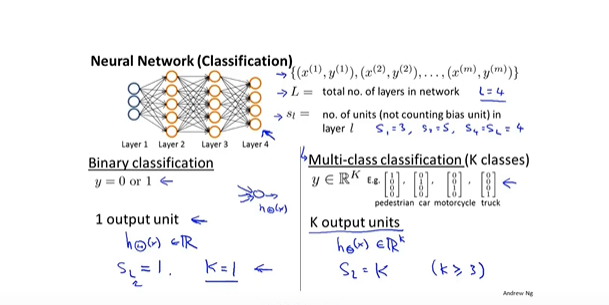
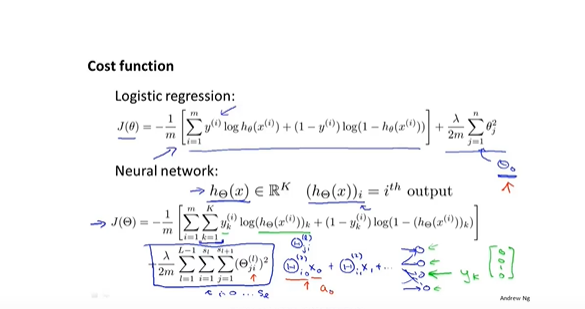
- 反向传播算法 *
- 优化目标

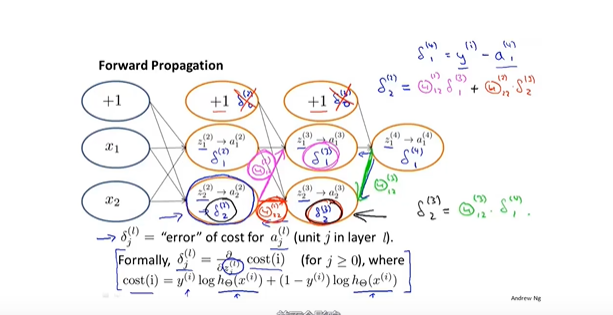
- 一个样本的向前传播计算

- 误差计算
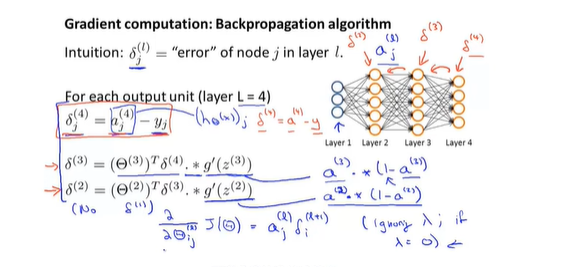

- 理解反向传播


4.理解向量和矩阵计算
- 向量和矩阵表达

- 矩阵向量转换


- 梯度检测:反向传播算法的实现容易出现Bug,通过梯度检测来验证算法实现上的正确性
- 思路:计算一点的割线斜率近似这点的导数,与计算出来的导数比较,验证导数计算的正确性
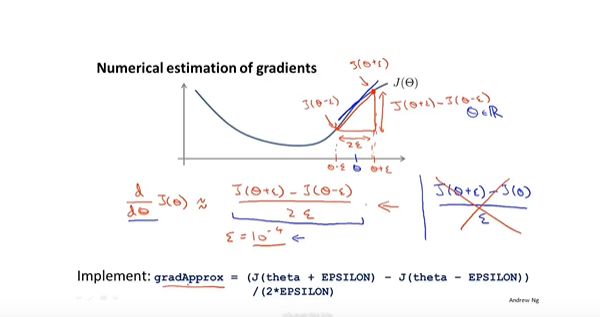

- 梯度检测代码和梯度下降代码结果验证

- 随机初始化
- 相同初始化如0导致无法正常梯度下降,只能得到相同的特征,对称性导致的结果,学习不到更复杂的函数
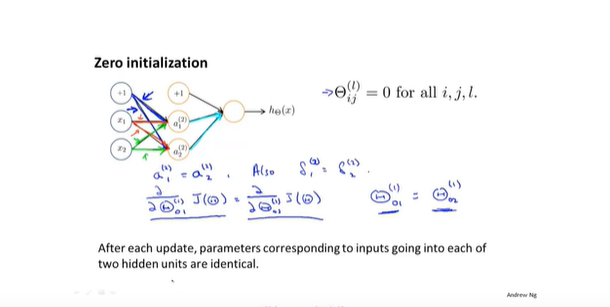
- 随机初始化权重

- 总结
- 选择一个神经网络架构
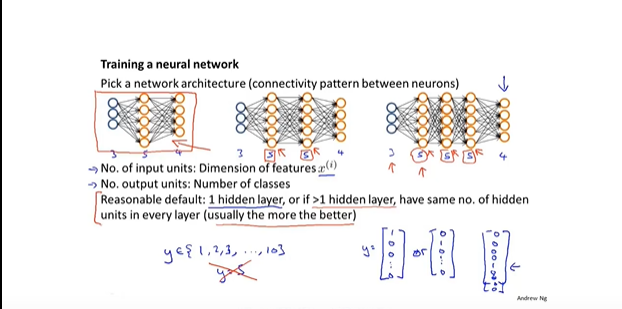
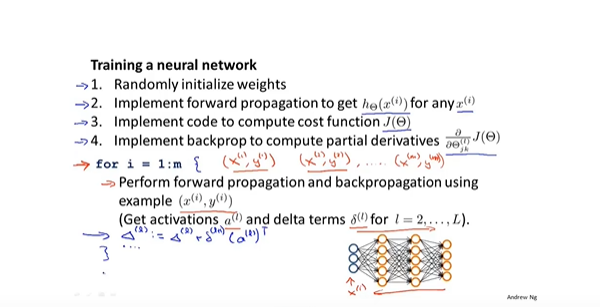
- 训练网络

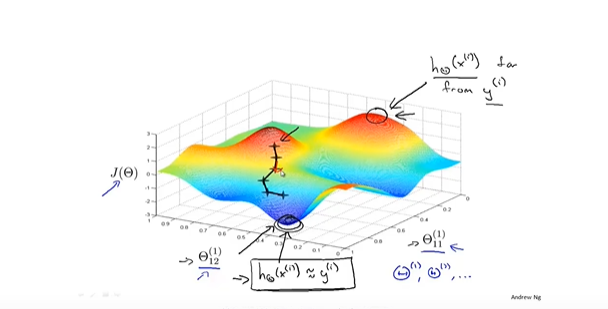
- 直观理解
- 自动驾驶,选择方向问题

参考

