吴恩达机器学习课程笔记3-分类和过拟合

6 分类

1. 简介

• 分类任务
  
• 线性回归应用于分类效果不好
  
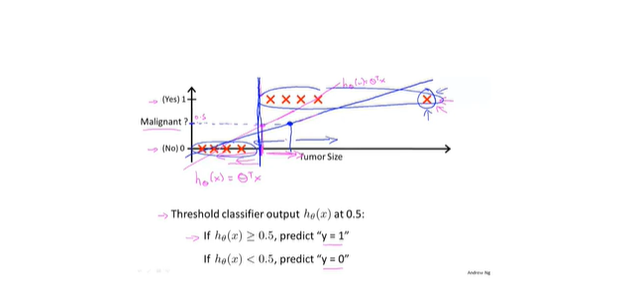
• 逻辑回归用于分类任务
  

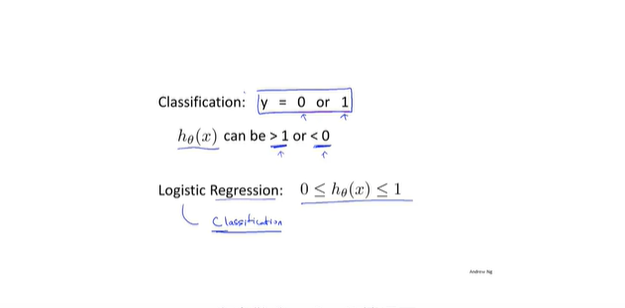
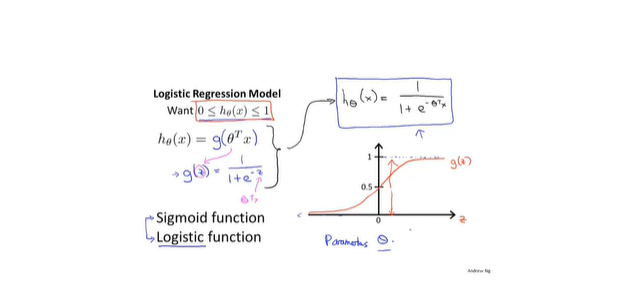
2. 激活函数

• 将线性值收敛到（0，1）之间，形成非线性值
  
• 概率解释
  

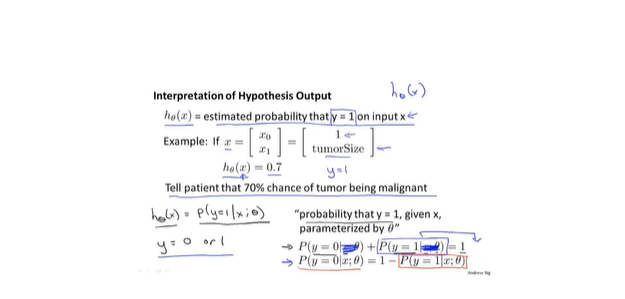
3. 决策边界

• 预测0和1
  
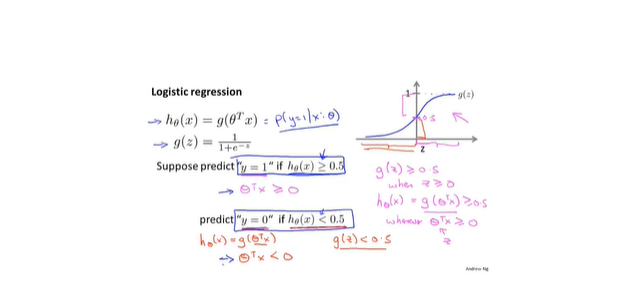
• 边界决策问题
  
  

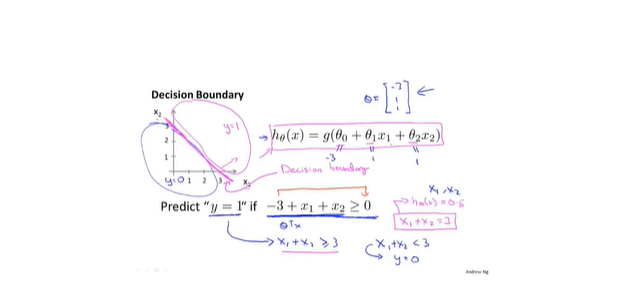
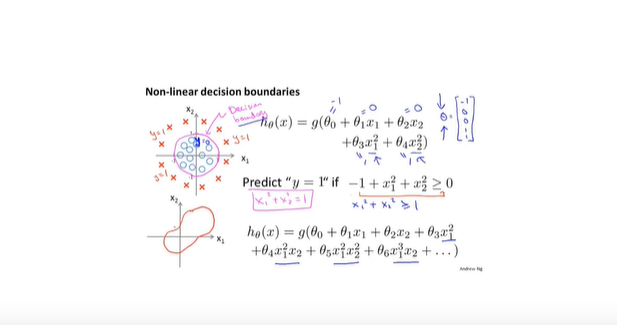
4. 损失函数
   

• 均方损失函数用于逻辑回归不易收敛(引入了非线性)
  
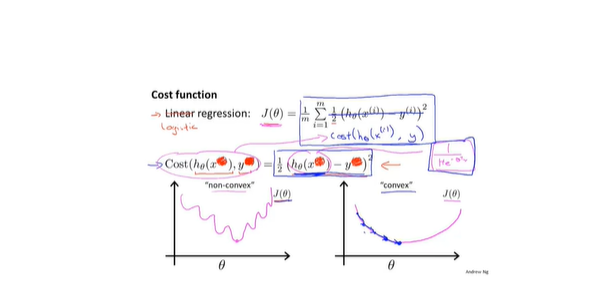
• 新损失函数: 函数性质非常符合损失函数，会使得损失函数是一个凸函数
  
  
  

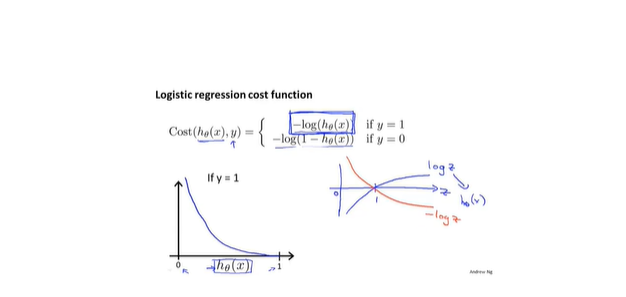
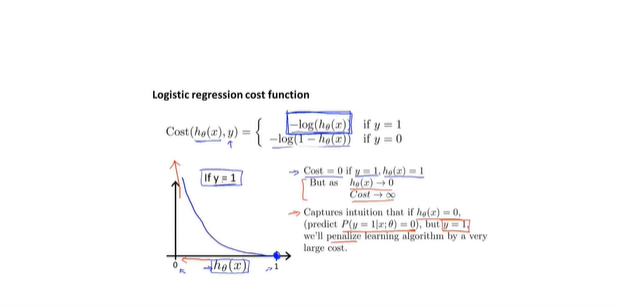
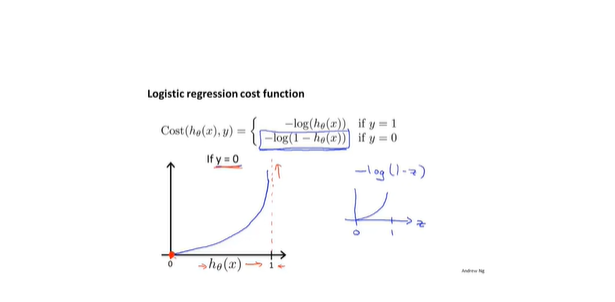
5. 简化损失函数和梯度下降
   
   
   

• 特征缩放也适用于逻辑回归

6. 高级优化:调用库去使用算法,优先选择高级算法
   
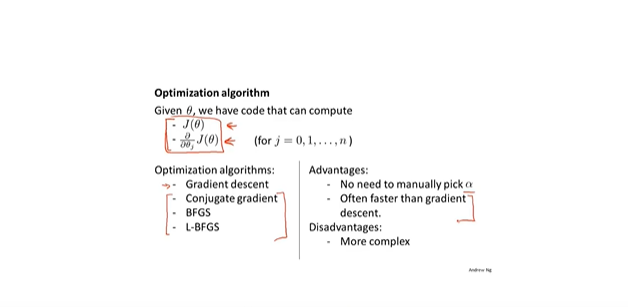
7. 一对多的多分类问题
   
   

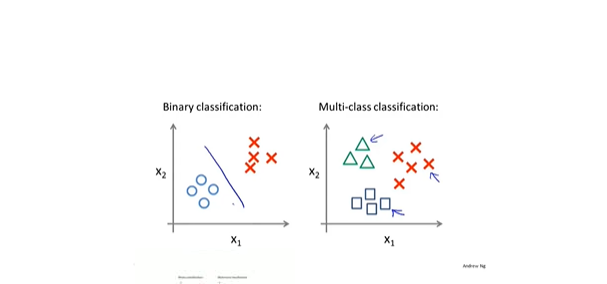
• 使用多个分类器进行分类取概率
  
  

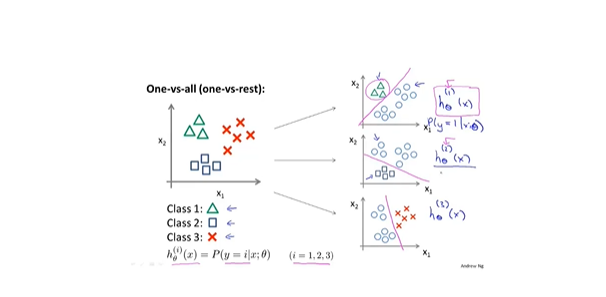
7 过拟合:overfitting

1. 过拟合现象

• 线性回归
  
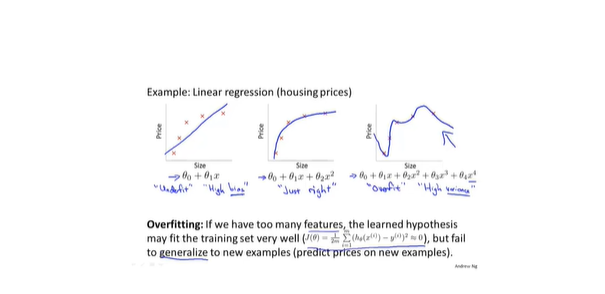
• 逻辑回归
  
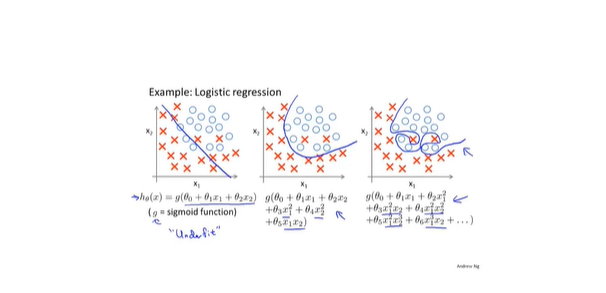
• 使用专门的工具发现过拟合和欠拟合问题
• 数据少，特征多，容易出现过拟合
• 解决方法:1. 降低特征数, 2.正则化
  

2. 正则化

• 如果每个特征都有用，那么不能减少特指数, n个特征据需要有n个权重(参数),多项式回归中容易产生过拟合，通过降低权重的值使之接近0,可以形成更简单的假设函数。
• 正则化思想，降低参数值使之接近0
  
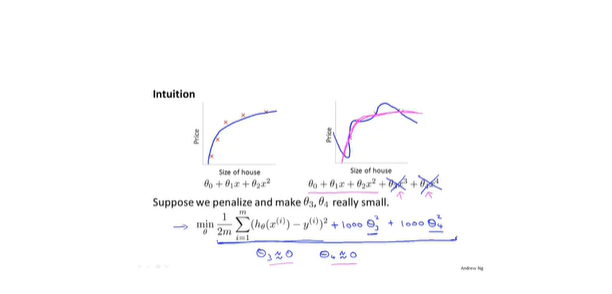
• 实现方法;并不知道对哪个参数进行降低，所以降低所有的参数值(不包括偏执项),添加惩罚项
  
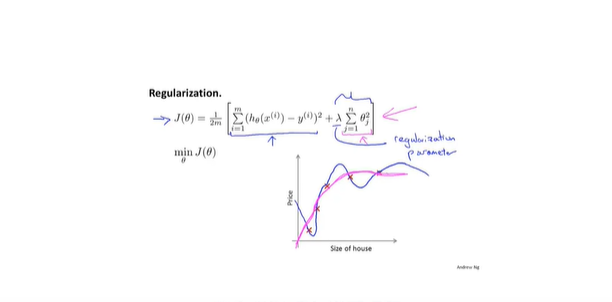
• 添加的参数值(lamt)应该是一个大数，通过训练能够得到更小的seta值,正则化参数也不能过大
  

3. 线性回归正则化
   

• 正则化在梯度下降中的作用: 每次将参数值降低一点再进行梯度下降
  
• 正规方程的正则化：还可以保证内部矩阵可逆
  

4. 逻辑回归中的正则化
   
   
   

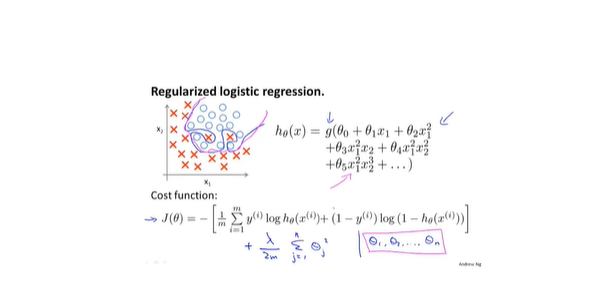
参考

• 视频课程