图的深度优先遍历和广度优先遍历

深度优先遍历简称DFS（Depth First Search），广度优先遍历简称BFS（Breadth First Search），它们是遍历图当中所有顶点的两种方式。

 

我们来到一个游乐场，游乐场里有11个景点。我们从景点0开始，要玩遍游乐场的所有景点，可以有什么样的游玩次序呢？

深度优先遍历

二叉树的前序、中序、后序遍历，本质上也可以认为是深度优先遍历。

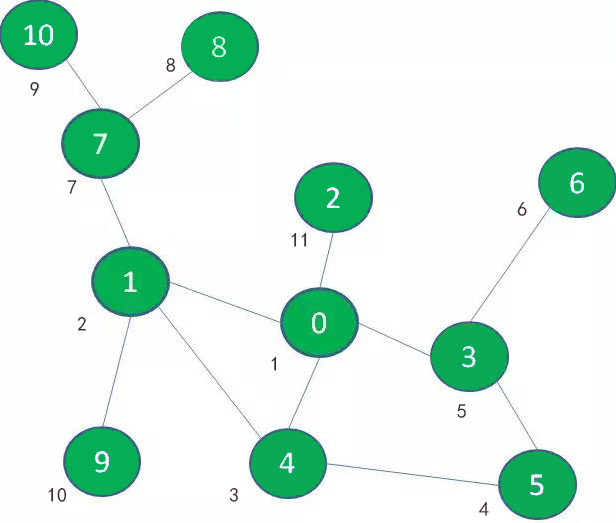
第一种是一头扎到底的玩法。我们选择一条支路，尽可能不断地深入，如果遇到死路就往回退，回退过程中如果遇到没探索过的支路，就进入该支路继续深入。

 

在图中，我们首先选择景点1的这条路，继续深入到景点4、景点5、景点3、景点6，终于发现走不动了（景点旁边的数字代表探索次序）：

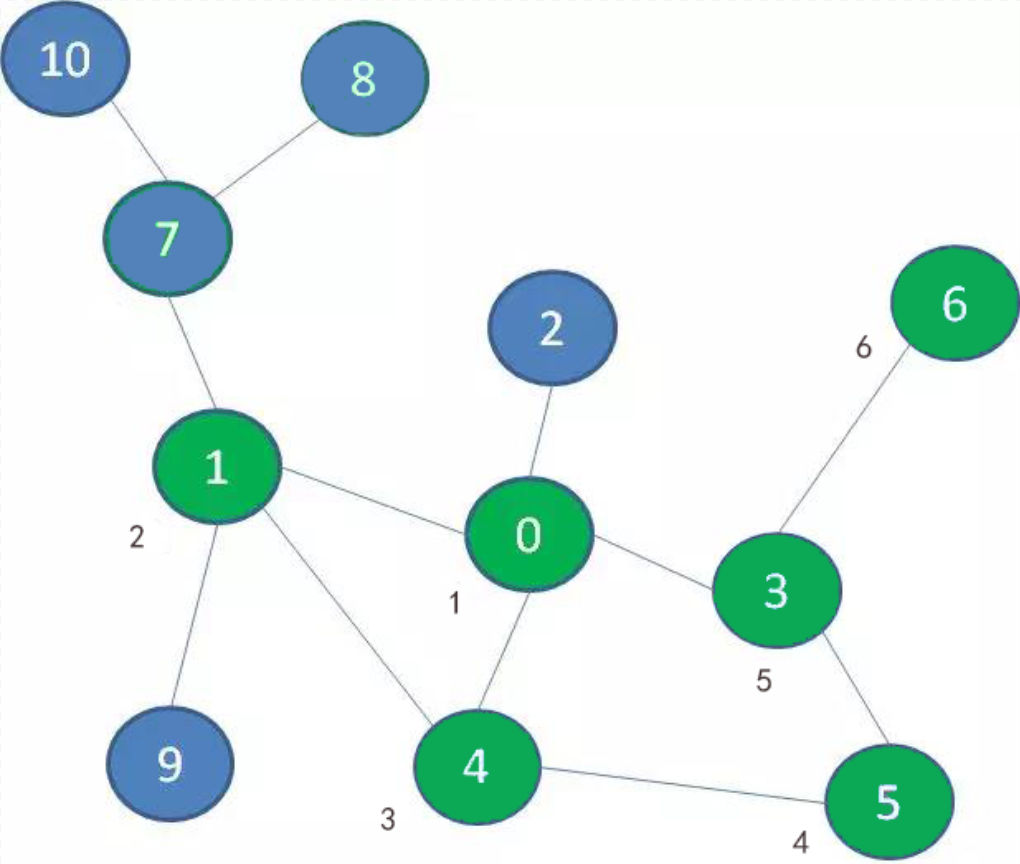
于是，我们退回到景点1，然后探索景点7，景点8，又走到了死胡同。于是，退回到景点7，探索景点10：

  

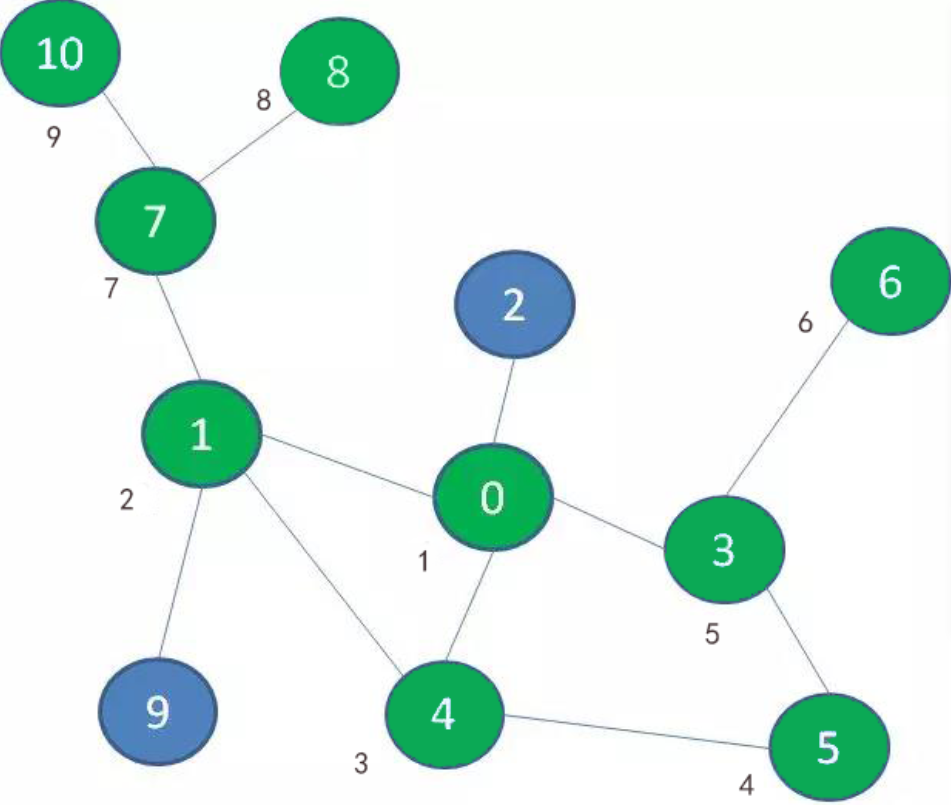
按照这个思路，我们再退回到景点1，探索景点9,最后再退回到景点0，后续依次探索景点2，终于玩遍了整个游乐场：

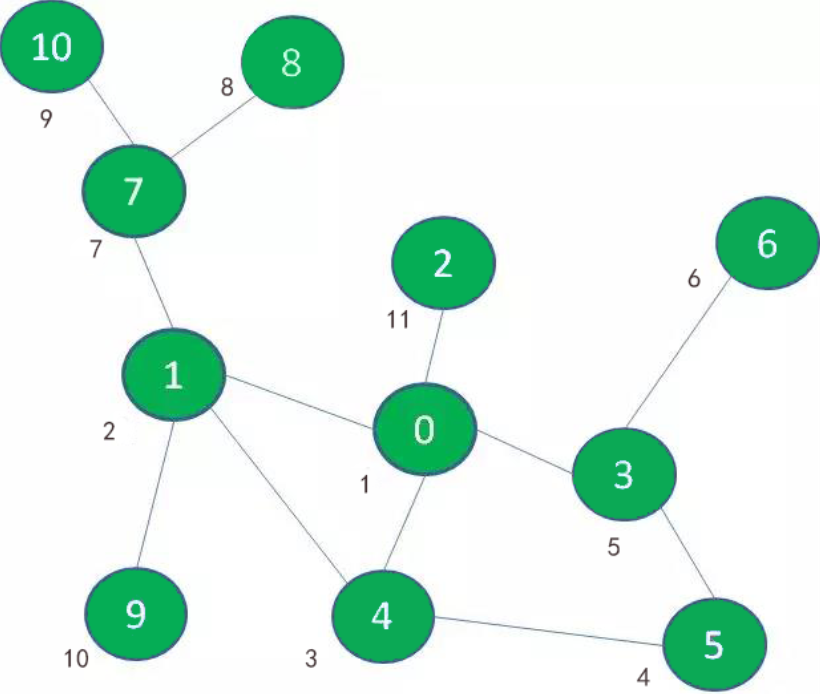
广度优先遍历

二叉树的层序遍历，本质上也可以认为是深度优先遍历。

在图中，我们首先探索景点0的相邻景点1、2、3、4

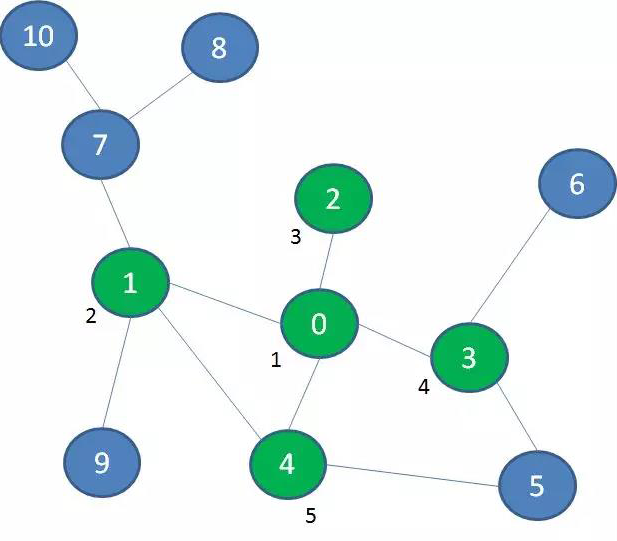
接着，我们探索与景点0相隔一层的景点7、9、5、6：

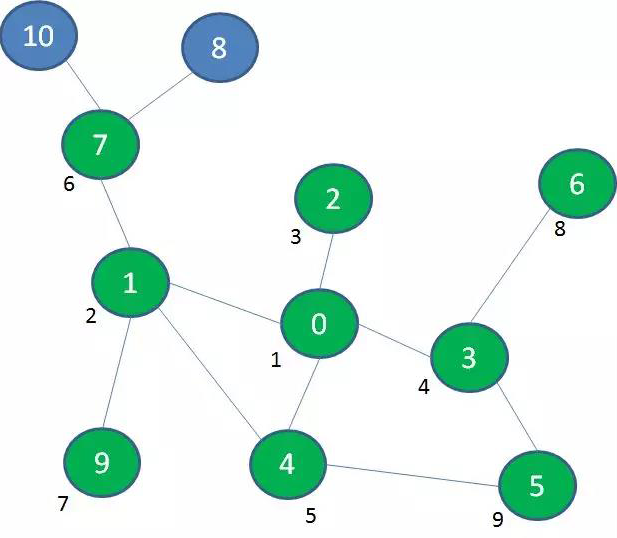
最后，我们探索与景点0相隔两层的景点8、10：

 

 

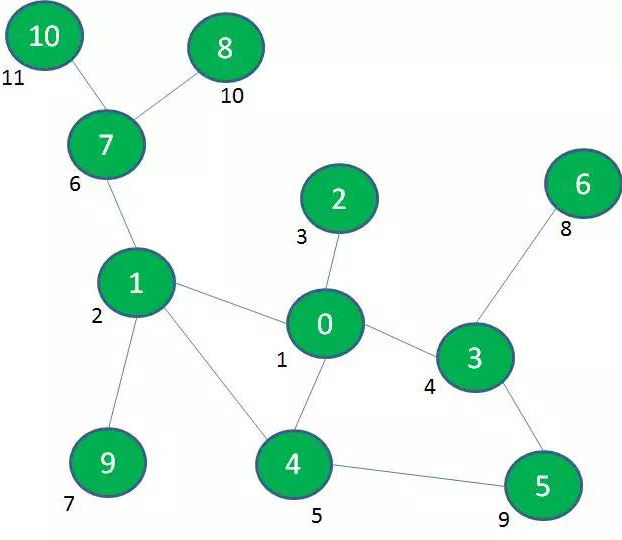
<?php
/**
 * 图的深度优先遍历、广度优先遍历
 * 图的存储结构--邻接矩阵
 */
class Graph {
    // 存储节点信息
    public $vertices;
    // 存储边信息
    public $arcs;
    // 图的节点数
    public $vexnum;
    // 记录节点是否已被遍历
    public $visited = [];

    // 初始化
    public function __construct($vertices) {
        $this->vertices = $vertices;
        $this->vexnum = count($this->vertices);
        for ($i = 0; $i < $this->vexnum; $i++) {
            for ($j = 0; $j < $this->vexnum; $j++) {
                $this->arcs[$i][$j] = 0;
            }
        }
    }

    // 两个顶点间添加边(无向图)
    public function addEdge($a, $b) {
        if ($a == $b) { // 边的头尾不能为同一节点
            return;
        }
        $this->arcs[$a][$b] = 1;
        $this->arcs[$b][$a] = 1;
    }

    // 从第i个节点开始深度优先遍历
    public function traverse($i) {
        // 标记第i个节点已遍历
        $this->visited[$i] = 1;
        // 打印当前遍历的节点
        echo $this->vertices[$i] . PHP_EOL;
        // 遍历邻接矩阵中第i个节点的直接联通关系
        for ($j = 0; $j < $this->vexnum ; $j++) {
            // 目标节点与当前节点直接联通，并且该节点还没有被访问，递归
            if ($this->arcs[$i][$j] == 1 && $this->visited[$j] == 0) {
                $this->traverse($j);
            }
        }
    }

    //深度优先遍历
    public function dfs() {
        // 初始化节点遍历标记
        $this->init();
        
        // 从没有被遍历的节点开始深度遍历
        for ($i = 0; $i < $this->vexnum; $i++) {
            if ($this->visited[$i] == 0) {
                // 若是连通图，只会执行一次
                $this->traverse($i);
            }
        }
    }
    
    // 初始化节点遍历标记
    public function init(){
        for ($i = 0; $i < $this->vexnum; $i++) {
            
            $this->visited[$i] = 0;
        }
    }
    
    //广度优先遍历
    public function bfs() {
        // 初始化节点遍历标记
        $this->init();
        
        $queue = [];
        for ($i = 0; $i < $this->vexnum; $i++) { // 对每一个顶点做循环
            if (!$this->visited[$i]) {      // 若是未访问过就处理
                $this->visited[$i] = 1;     // 设置当前顶点访问过
                echo $this->vertices[$i] . PHP_EOL;   // 打印顶点
                $queue[] = $i;              // 将此顶点入队列
                while (!empty($queue)) {    // 若当前队列不为空
                    $curr = array_shift($queue);    // 将队对元素出队
                    for ($j = 0; $j < $this->vexnum; $j++) {
                        if ($this->arcs[$curr][$j] == 1 && $this->visited[$j] == 0) {
                            $this->visited[$j] = 1; // 将找到的此顶点标记为已访问
                            echo $this->vertices[$j] . PHP_EOL;   // 打印顶点
                            $queue[] = $j;          // 将找到的此顶点入队列
                        }
                    }
                }
            }
        }
    }
}

/*
   0 1 2 3 4 5 6 7 8 9 10
0  0 1 1 1 1 0 0 0 0 0 0
1  1 0 0 0 1 0 0 1 0 1 0 
2  1 0 0 0 0 0 0 0 0 0 0
3  1 0 0 0 0 1 1 0 0 0 0
4  1 1 0 0 0 1 0 0 0 0 0
5  0 0 0 1 1 0 0 0 0 0 0
6  0 0 0 1 0 0 0 0 0 0 0
7  0 1 0 0 0 0 0 0 1 0 1
8  0 0 0 0 0 0 0 1 0 0 0
9  0 1 0 0 0 0 0 0 0 0 0
10 0 0 0 0 0 0 0 1 0 0 0

so
0 1,2,3,4
1 0,4,7,9
2 0
3 0,5,6
4 0,1,5
5 3,4
6 3
7 1,8,10
8 7
9 1
10 7
*/
// 测试
$vertices = ['景点0', '景点1', '景点2', '景点3', '景点4', '景点5', '景点6', '景点7', '景点8', '景点9', '景点10'];
$graph = new Graph($vertices);
$graph->addEdge(0, 1);
$graph->addEdge(0, 2);
$graph->addEdge(0, 3);
$graph->addEdge(0, 4);
$graph->addEdge(1, 4);
$graph->addEdge(1, 7);
$graph->addEdge(1, 9);
$graph->addEdge(3, 5);
$graph->addEdge(3, 6);
$graph->addEdge(4, 5);
$graph->addEdge(7, 8);
$graph->addEdge(7, 10);
// 递归
echo "dfs:";
$graph->dfs();

echo "<br />";
echo "bfs:";
$graph->bfs();