Codeforces Round #556 (Div. 2) - C. Prefix Sum Primes（思维）

Problem  Codeforces Round #556 (Div. 2) - D. Three Religions

Time Limit: 1000 mSec

Problem Description

 

Input

 

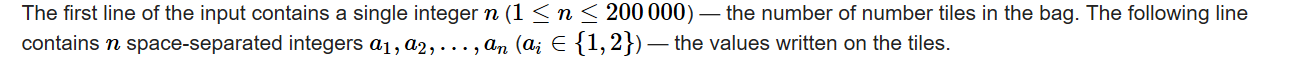
Output

 

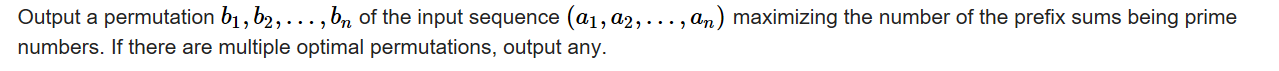
Sample Input

5
1 2 1 2 1

Sample Output

1 1 1 2 2

 

题解：这个题有做慢了，这种题做慢了和没做出来区别不大。。。

　　读题的时候脑子里还意识到素数除了2都是奇数，读完之后就脑子里就只剩欧拉筛了，贪心地构造使得前缀和是连续的素数，那实现就很简单了，将素数序列的差分序列求出来，不断凑出差分序列的每个数即可，但是之后想想，除了2 和 3，每个的间隔不都是偶数么，肯定是连续的2呀，费劲算差分序列干什么，直接先放2再放1不就行了（特殊处理一下2 和 3 即可），写着写着还误以为要输出下标，临时改了改，等到测样例的时候发现是输出1、2，暴风哭泣。

#include <bits/stdc++.h>

using namespace std;

#define REP(i, n) for (int i = 1; i <= (n); i++)
#define sqr(x) ((x) * (x))

const int maxn = 400000 + 10000;
const int maxm = 200000 + 100;
const int maxs = 10000 + 10;

typedef long long LL;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;

const LL unit = 1LL;
const int INF = 0x3f3f3f3f;
const double eps = 1e-14;
const double inf = 1e15;
const double pi = acos(-1.0);
const int SIZE = 100 + 5;
const LL MOD = 1000000007;

LL n;
LL a[maxn];
int cnt[5];
LL cnt1, cnt2;
LL tot, prime[maxn];
bool is_prime[maxn];

void Euler()
{
    memset(is_prime, true, sizeof(is_prime));
    is_prime[0] = is_prime[1] = false;
    for (LL i = 2; i < maxn; i++)
    {
        if (is_prime[i])
        {
            prime[tot++] = i;
        }
        for (LL j = 0; j < tot && i * prime[j] < maxn; j++)
        {
            is_prime[prime[j] * i] = false;
            if (i % prime[j] == 0)
            {
                break;
            }
        }
    }
}

vector<int> ans;
queue<int> que[3];

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    //freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
    Euler();
    cin >> n;
    int x;
    LL sum = 0;
    for (int i = 1; i <= n; i++)
    {
        cin >> x;
        que[x].push(i);
        cnt[x]++;
        sum += x;
    }
    cnt1 = cnt[1], cnt2 = cnt[2];
    LL pre = 0;
    for (int i = 0; i < tot && prime[i] <= sum; i++)
    {
        LL tmp = prime[i] - pre;
        LL x = tmp / 2;
        x = min(x, cnt2);
        if (tmp - x * 2 <= cnt1)
        {
            pre = prime[i];
            for (int j = 0; j < x; j++)
            {
                ans.push_back(2);
            }
            for (int j = 0; j < tmp - x * 2; j++)
            {
                ans.push_back(1);
            }
            cnt2 -= x;
            cnt1 -= (tmp - x * 2);
        }
    }
    for(int i = 0; i < ans.size(); i++)
    {
        cout << ans[i] << " ";
    }
    while(cnt1--)
    {
        cout << 1 << " ";
    }
    while(cnt2--)
    {
        cout << 2 << " ";
    }
    return 0;
}