查找
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 吕以晴 |
0.PTA得分截图
查找题目集总得分,请截图,截图中必须有自己名字。题目至少完成总题数的2/3,否则本次作业最高分5分。没有全部做完扣1分。
1.本周学习总结(0-5分)
1.1 查找的性能指标
ASL成功、不成功,比较次数,移动次数、时间复杂度
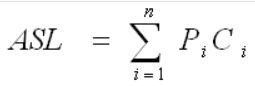
其中n为查找表中元素个数,Pi为查找第i个元素的概率,通常假设每个元素查找概率相同,Pi=1/n,Ci是找到第i个元素的比较次数。
-
ASL
- ASL,是查找算法的查找成功时的平均查找长度的缩写,是为确定记录在查找表中的位置,需和给定值进行比较的关键字个数的期望值。
- ASL是衡量查找算法性能好坏的重要指标。一个查找算法的ASL越大,其时间性能越差;反之,一个查找算法的ASL越小,其时间性能越好。
-
ASL成功与失败
- 查找方式为从头扫到尾,找到待查找元素即查找成功,若到尾部没有找到,说明查找失败。
-
顺序查找平均比较次数
(n+1)/2 -
顺序查找的平均移动次数
- 插入:n/2
- 删除:(n-1)/2
-
时间复杂度
- 顺序查找:
(1)最好情况:要查找的第一个就是。时间复杂度=O(1)
(2)最坏情况:最后一个是要查找的元素。时间复杂度=O(n)
(3)平均情况下就是:(n+1)/2。
所以总的来说时间复杂度为:O(n) - 二分查找:O(log2n)
- 顺序查找:
1.2 静态查找
分析静态查找几种算法包括:顺序查找、二分查找的成功ASL和不成功ASL。
顺序查找
int SeqSearch(int s[],int n,int key)
{
int i;
for(i=0;s[i]!=key;i++);
if(i<n)
return i;
else
return -1;
}
- 从表的一端开始,顺序扫描线性表,依次将扫描到的关键字与给定值k相比较。
若扫描到的关键字=k,则查找成功;若扫描结束,仍未找到关键字=k,则查找失败。 - Ci(第i个元素的比较次数)在于这个元素在查找表中的位置,如第0号元素就需要比较一次,第一号元素比较2次......第n号元素要比较n+1次。所以Ci=i。
1 2 3 4 5 6 7 8
- 若查找k=3,则ASL成功=3
- 若查找k=20,则ASL不成功=8
- 适用情形
- 算法简单,对查找表结构无任何要求,有序与否都行。
- n太大时,查找效率低。
二分查找
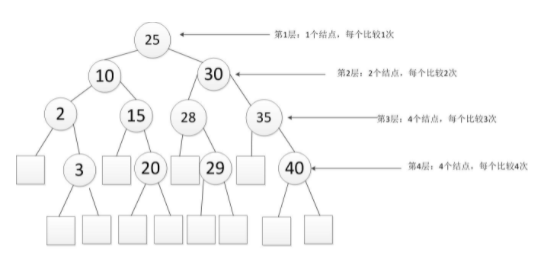
ASL成功=(1*1+2*2+4*3+4*4)/11=3ASL失败=(4*3+8*4)/12=3.67- 适用情形
- 比较次数少,查找效率高,只用于顺序存储的有序表。
- 不适用于经常修改操作(删除插入等)。
int Search_Bin(SSTable *ST,keyType key){
int low=1;//初始状态 low 指针指向第一个关键字
int high=ST->length;//high 指向最后一个关键字
int mid;
while (low<=high) {
mid=(low+high)/2;//int 本身为整形,所以,mid 每次为取整的整数
if (ST->elem[mid].key==key)//如果 mid 指向的同要查找的相等,返回 mid 所指向的位置
{
return mid;
}else if(ST->elem[mid].key>key)//如果mid指向的关键字较大,则更新 high 指针的位置
{
high=mid-1;
}
//反之,则更新 low 指针的位置
else{
low=mid+1;
}
}
return 0;
}
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树(操作)
结合一组数据介绍构建过程,及二叉搜索树的ASL成功和不成功的计算方法。
构建二叉搜索树
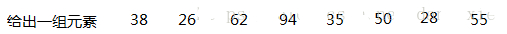
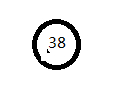
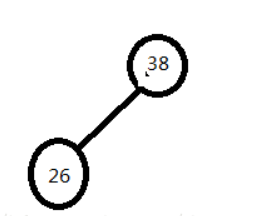
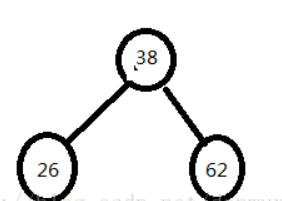
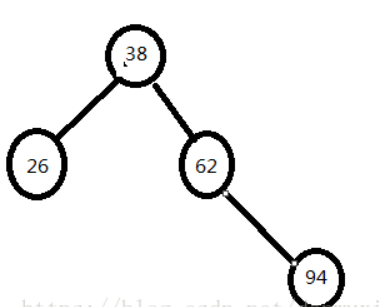
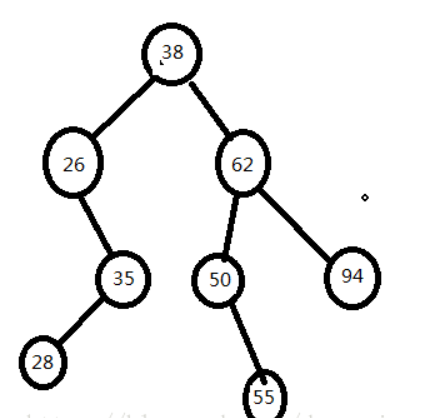
- ASL成功=(11+22+33+42)/8=2.75
- ASL不成功=(21+34+4*4)/9=3.33
插入
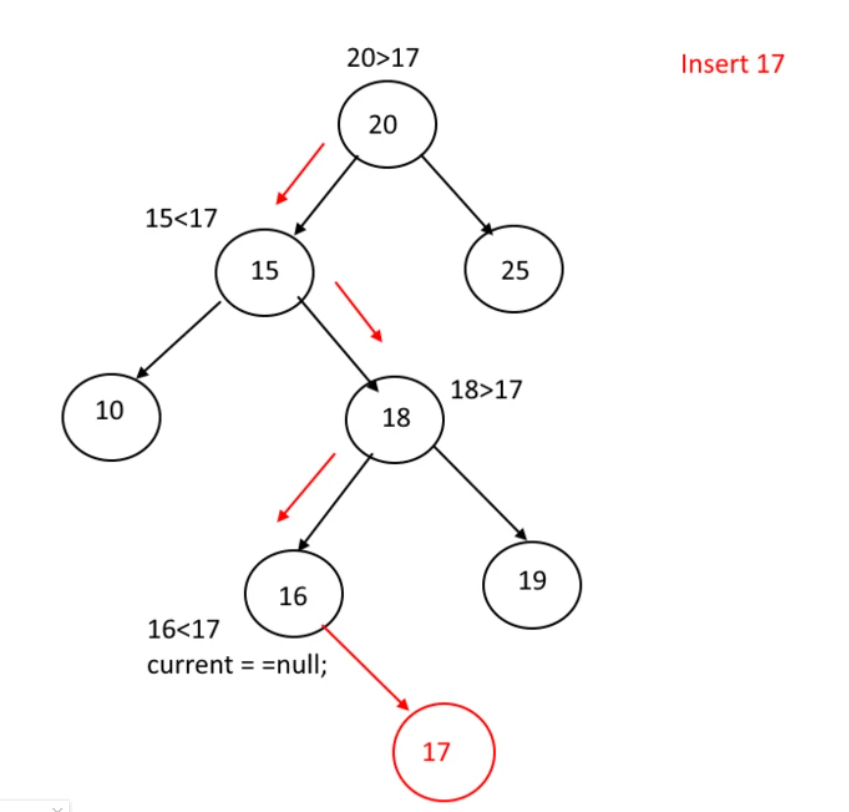
删除
- 假设要删的是e,此时待删元素没有左右子树,可以直接删除,将其父节点指向空
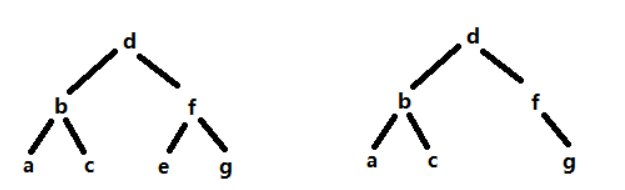
-
假设要删的是f,此时待删除的元素只有右子树,将待删除结点的父节点指向待删除结点的右子树即可
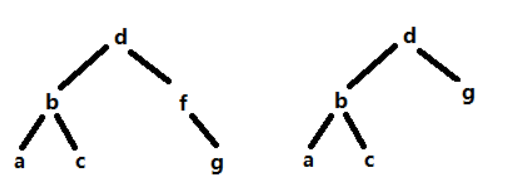
-
假设要删的是b,此时待删除的元素左右子树均存在,那么我们将该节点与其右子树上最小的一个节点交换,然后转为删掉最小的那一个元素c。
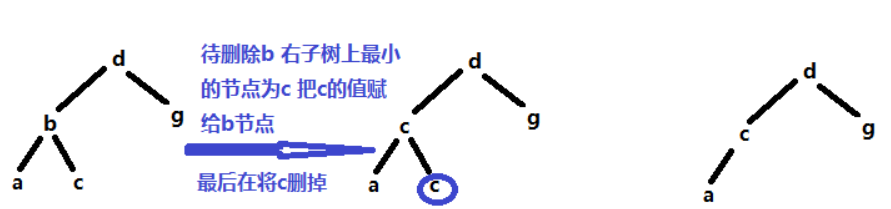
-
假设要删的是c,此时待删除的元素只有左子树,我们直接将待删除节点的父节点指向待删除节点的左子树即可。
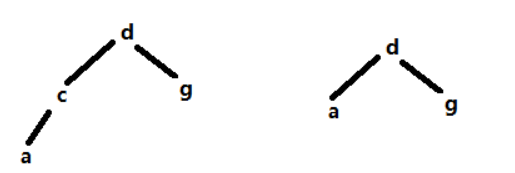
1.3.2 如何构建二叉搜索树(代码)
- 如何构建、插入、删除及代码。
①插入
int BSTreeNodeInsertR(BSTreeNode **tree,DataType x) //搜索树的插入
{
if(*tree == NULL)
{
*tree = BuyTreeNode(x);
return 0;
}
if ((*tree)->_data > x)
return BSTreeNodeInsertR(&(*tree)->_left,x);
else if ((*tree)->_data < x)
return BSTreeNodeInsertR(&(*tree)->_right,x);
else
return -1;
}
②删除
BSTNode* SearchNode(BSTree bt, KeyType k)//搜索树的删除
{
if (bt == NULL || bt->key == k)
return bt;
else if (bt->key < k)
return SearchNode(bt->rchild, k);
else
return SearchNode(bt->child, k);
}
③查找
BSTreeNode *BSTreeNodeFindR(BSTreeNode *tree,DataType x)//搜索树的查找
{
if (!tree)
return NULL;
if (tree->_data > x)
BSTreeNodeFindR(tree->_left,x);
else if (tree->_data < x)
BSTreeNodeFindR(tree->_right,x);
else
return tree;
}
-
2.分析代码的时间复杂度
最好:O(logn),最差:O(n) -
3.为什么要用递归实现插入、删除?递归优势体现在代码哪里?
- 使用递归可以使代码更简洁清晰,可读性更好
- 在树的遍历运算中,递归的实现明显要比循环简单得多。
1.4 AVL树
AVL树解决什么问题,其特点是什么?
- 解决问题
解决的是动态问题,静态的查找无需平衡树,一般排序+二分或线段树即可。 - 特点
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
结合一组数组,介绍AVL树的4种调整做法。
-
LL
- 图①结点x和结点a变换,则树平衡了。
- x>d,d>a,所以d可作为x的左孩子。且可作为a的右孩子中的孩子
实现:找到根结点x,与它的左孩子a进行交换就可以使二叉树树再次平衡

-
RR
- 找到根结点x,与它的右孩子a进行交换就可以使二叉树树再次平衡
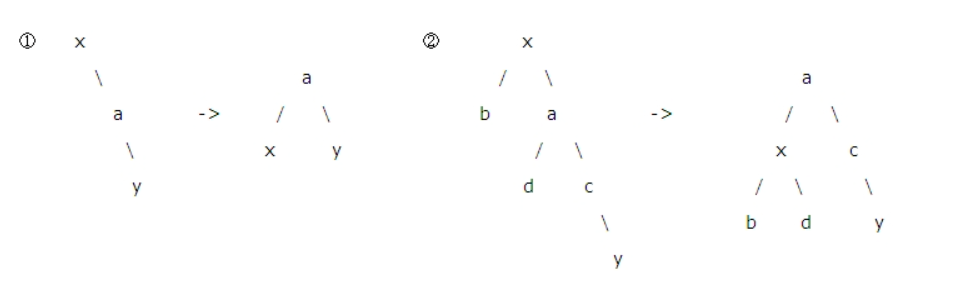
- 找到根结点x,与它的右孩子a进行交换就可以使二叉树树再次平衡
-
LR
- 这个左右和下边的右左,略微复杂了点。须要进行两次交换。才干达到平衡,注意这时y是c的右孩子。终于y作为x的左孩子。若y是c的左孩子。终于y作为a
的右孩子。
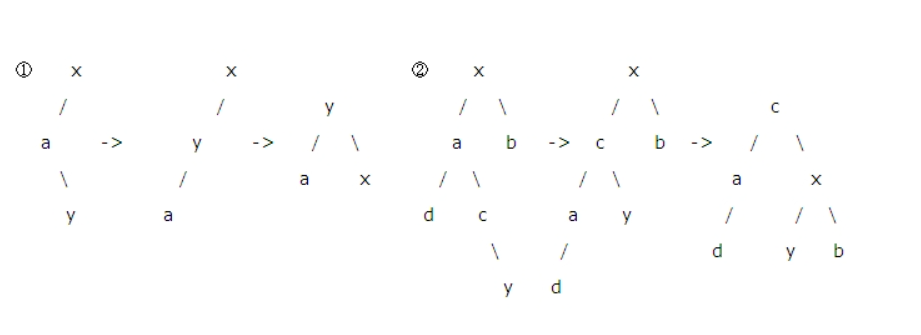
- 这个左右和下边的右左,略微复杂了点。须要进行两次交换。才干达到平衡,注意这时y是c的右孩子。终于y作为x的左孩子。若y是c的左孩子。终于y作为a
-
RL
- 找到根结点x,让x的右孩子a与x的右孩子a的左孩子c进行交换,然后再让x与x此时的右孩子c进行交换。终于达到平衡;
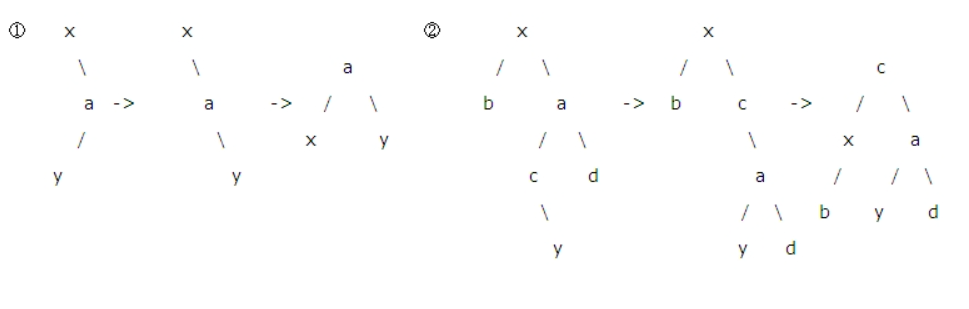
- 找到根结点x,让x的右孩子a与x的右孩子a的左孩子c进行交换,然后再让x与x此时的右孩子c进行交换。终于达到平衡;
AVL树的高度和树的总节点数n的关系?
h≈log2N(h)+1
介绍基于AVL树结构实现的STL容器map的特点、用法。
Map是STL的一个关联容器,它提供一对一(其中第一个可以称为关键字,每个关键字只能在map中出现一次,第二个可能称为该关键字的值)的数据处理能力,由于这个特性,它完成有可能在我们处理一对一数据的时候,在编程上提供快速通道。map内部自建一颗红黑树(一种非严格意义上的平衡二叉树),这颗树具有对数据自动排序的功能,所以在map内部所有的数据都是有序的
mymap.insert ( std::pair<char,int>('a',100) );
mymap.insert ( std::pair<char,int>('z',200) );
std::pair<std::map<char,int>::iterator,bool> ret;
ret = mymap.insert ( std::pair<char,int>('z',500) );if(ret.second==false) {
std::cout <<"element 'z' already existed";
std::cout <<" with a value of "<< ret.first->second <<'\n';
}
- 数据的查找(包括判定这个关键字是否在map中出现)
在这里我们将体会,map在数据插入时保证有序的好处。
要判定一个数据(关键字)是否在map中出现的方法比较多,这里标题虽然是数据的查找,在这里将穿插着大量的map基本用法。
这里给出三种数据查找方法
-
第一种:用count函数来判定关键字是否出现,其缺点是无法定位数据出现位置,由于map的特性,一对一的映射关系,就决定了count函数的返回值只有两个,要么是0,要么是1,出现的情况,当然是返回1了
-
第二种:用find函数来定位数据出现位置,它返回的一个迭代器,当数据出现时,它返回数据所在位置的迭代器,如果map中没有要查找的数据,它返回的迭代器等于end函数返回的迭代器。
-
数据的清空与判空
清空map中的数据可以用clear()函数,判定map中是否有数据可以用empty()函数,它返回true则说明是空map
- 数据的删除
Map<int,string> mapStudent;
mapStudent.insert(pair<int,string>(1,“student_one”));
mapStudent.insert(pair<int,string>(2,“student_two”));
mapStudent.insert(pair<int,string>(3,“student_three”));
//如果你要演示输出效果,请选择以下的一种,你看到的效果会比较好
//如果要删除1,用迭代器删除
map<int,string>::iterator iter;
iter = mapStudent.find(1);
mapStudent.erase(iter);
//如果要删除1,用关键字删除
Int n = mapStudent.erase(1);//如果删除了会返回1,否则返回0
//用迭代器,成片的删除
//一下代码把整个map清空
mapStudent.earse(mapStudent.begin(),mapStudent.end());
//成片删除要注意的是,也是STL的特性,删除区间是一个前闭后开的集合
- 注意事项
-
List特点:元素有放入顺序,元素可重复
-
Set特点:元素无放入顺序,元素不可重复(注意:元素虽然无放入顺序,但是元素在set中的位置是有该元素的HashCode决定的,其位置其实是固定的)
-
Map特点:元素按键值对存储,无放入顺序 (应该知道什么是键值对吧!)
-
List接口有三个实现类:LinkedList,ArrayList,Vector
-
LinkedList:底层基于链表实现,链表内存是散乱的,每一个元素存储本身内存地址的同时还存储下一个元素的地址。链表增删快,查找慢
-
ArrayList和Vector的区别:ArrayList是非线程安全的,效率高;Vector是基于线程安全的,效率低
-
Set接口有两个实现类:HashSet(底层由HashMap实现),LinkedHashSet
-
SortedSet接口有一个实现类:TreeSet(底层由平衡二叉树实现)
-
Query接口有一个实现类:LinkList
-
Map接口有三个实现类:HashMap,HashTable,LinkeHashMap
-
HashMap非线程安全,高效,支持null;HashTable线程安全,低效,不支持null
-
SortedMap有一个实现类:TreeMap
-
list是用来处理序列的,而set是用来处理集的。Map是知道的,存储的是键值对
-
set 一般无序不重复.map kv 结构 list 有序。
-
1.5 B-树和B+树
B-树和AVL树区别
AVL树结点仅能存放一个关键字,树的高度较大,而B-树的一个结点可以存放多个关键字,降低了树的高度,可以解决大数据下的查找。
B-树解决什么问题?
B-树中关键字集合分布在整颗树中,叶节点中不包含任何关键字信息,只适合随机检索
B-树定义及特点
- 根节点至少有两个子女
- 每个中间节点都包含k-1个元素和k个孩子,其中m/2<=k<=m
- 每个叶子节点都包含k-1元素,其中m/2<=k<=m
- 所有的叶子节点都位于同一层
- 每个节点的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
B-树的插入
插入操作是指插入一条记录,即(key, value)的键值对。如果B树中已存在需要插入的键值对,则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。
1)根据要插入的key的值,找到叶子结点并插入。
2)判断当前结点key的个数是否小于等于m-1,若满足则结束,否则进行第3步。
3)以结点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父结点中,这个key的左子树指向分裂后的左半部分,这个key的右子支指向分裂后的右半部分,然后将当前结点指向父结点,继续进行第3步。
下面以5阶B树为例,介绍B树的插入操作,在5阶B树中,结点最多有4个key,最少有2个key
a)在空树中插入39

此时根结点就一个key,此时根结点也是叶子结点
b)继续插入22,97和41

根结点此时有4个key
c)继续插入53

插入后超过了最大允许的关键字个数4,所以以key值为41为中心进行分裂,结果如下图所示,分裂后当前结点指针指向父结点,满足B树条件,插入操作结束。当阶数m为偶数时,需要分裂时就不存在排序恰好在中间的key,那么我们选择中间位置的前一个key或中间位置的后一个key为中心进行分裂即可。
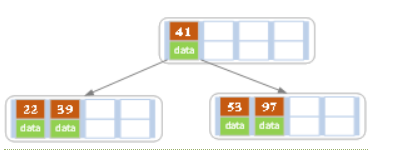
d)依次插入13,21,40,同样会造成分裂,结果如下图所示。
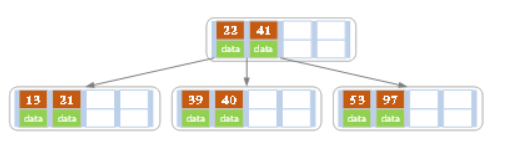
e)依次插入30,27, 33 ;36,35,34 ;24,29,结果如下图所示。
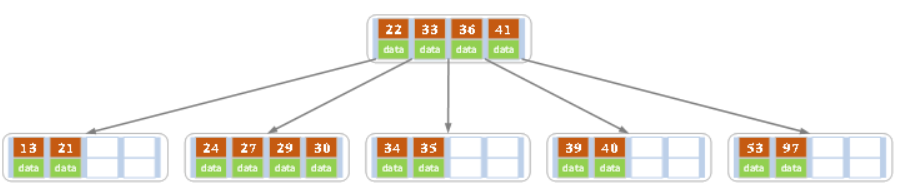
f)插入key值为26的记录,插入后的结果如下图所示。
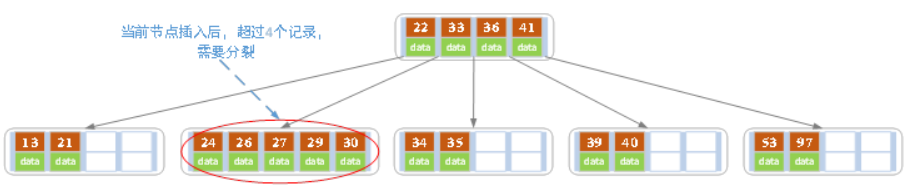
当前结点需要以27为中心分裂,并向父结点进位27,然后当前结点指向父结点,结果如下图所示。

进位后导致当前结点(即根结点)也需要分裂,分裂的结果如下图所示。
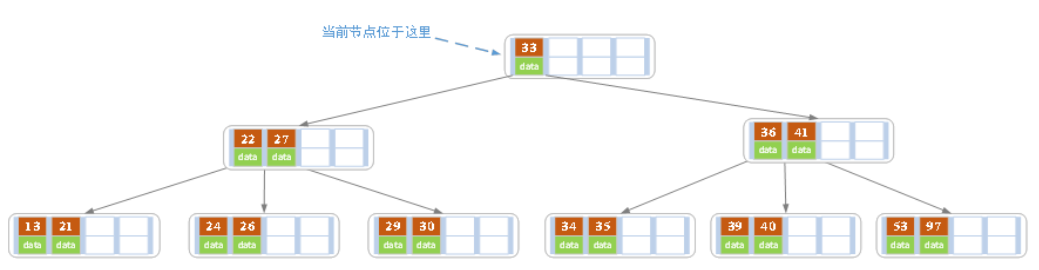
分裂后当前结点指向新的根,此时无需调整。
g)最后再依次插入key为17,28,29,31,32的记录,结果如下图所示。
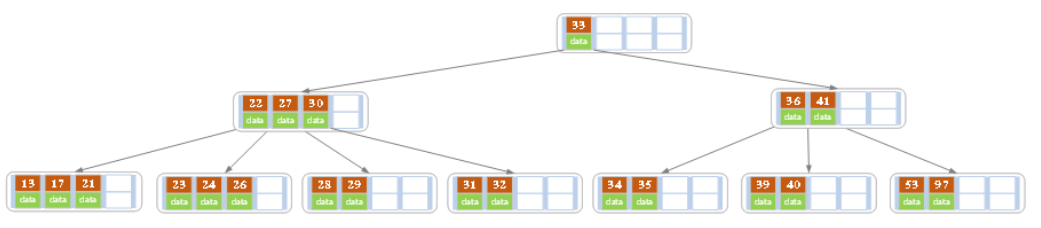
tips:
在实现B树的代码中,为了使代码编写更加容易,我们可以将结点中存储记录的数组长度定义为m而非m-1,这样方便底层的结点由于分裂向上层插入一个记录时,上层有多余的位置存储这个记录。同时,每个结点还可以存储它的父结点的引用,这样就不必编写递归程序。
B-树删除
删除操作是指,根据key删除记录,如果B树中的记录中不存对应key的记录,则删除失败。
1)如果当前需要删除的key位于非叶子结点上,则用后继key(这里的后继key均指后继记录的意思)覆盖要删除的key,然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上,这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步
2)该结点key个数大于等于Math.ceil(m/2)-1,结束删除操作,否则执行第3步。
3)如果兄弟结点key个数大于Math.ceil(m/2)-1,则父结点中的key下移到该结点,兄弟结点中的一个key上移,删除操作结束。
否则,将父结点中的key下移与当前结点及它的兄弟结点中的key合并,形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,重复上第2步。
有些结点它可能即有左兄弟,又有右兄弟,那么我们任意选择一个兄弟结点进行操作即可。
下面以5阶B树为例,介绍B树的删除操作,5阶B树中,结点最多有4个key,最少有2个key
a)原始状态
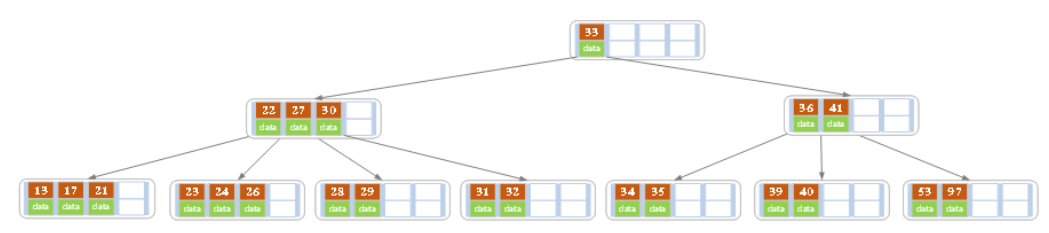
b)在上面的B树中删除21,删除后结点中的关键字个数仍然大于等2,所以删除结束。
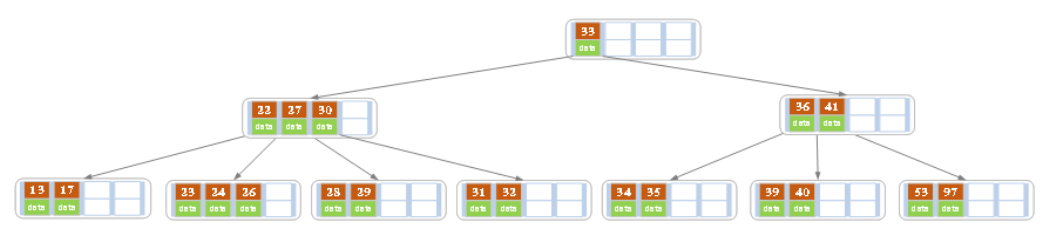
c)在上述情况下接着删除27。从上图可知27位于非叶子结点中,所以用27的后继替换它。从图中可以看出,27的后继为28,我们用28替换27,然后在28(原27)的右孩子结点中删除28。删除后的结果如下图所示。
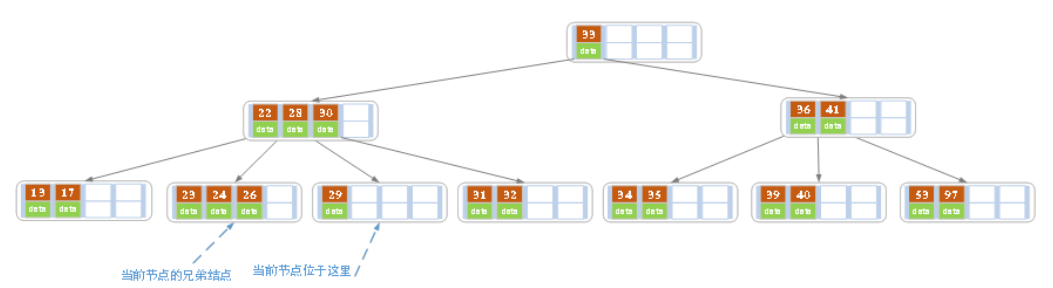
删除后发现,当前叶子结点的记录的个数小于2,而它的兄弟结点中有3个记录(当前结点还有一个右兄弟,选择右兄弟就会出现合并结点的情况,不论选哪一个都行,只是最后B树的形态会不一样而已),我们可以从兄弟结点中借取一个key。所以父结点中的28下移,兄弟结点中的26上移,删除结束。结果如下图所示。
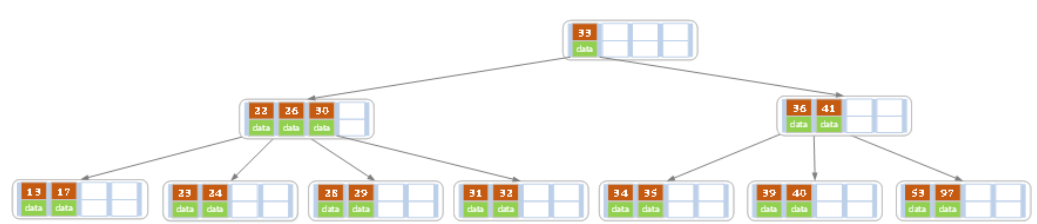
d)在上述情况下接着32,结果如下图。
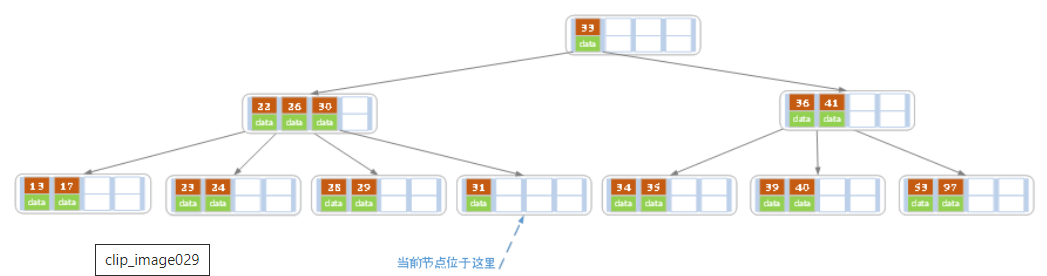
当删除后,当前结点中只key,而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并,成为一个新的结点,当前结点的指针指向父结点。结果如下图所示。
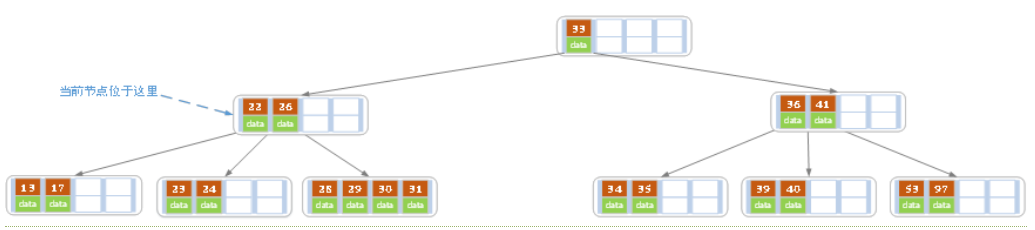
当前结点key的个数满足条件,故删除结束。
e)上述情况下,我们接着删除key为40的记录,删除后结果如下图所示。
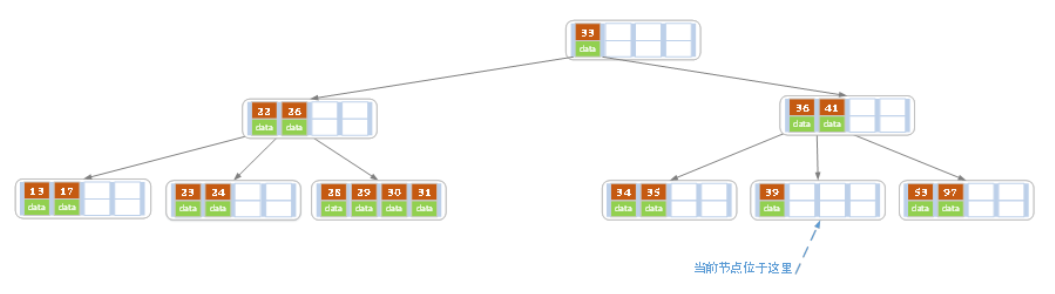
同理,当前结点的记录数小于2,兄弟结点中没有多余key,所以父结点中的key下移,和兄弟(这里我们选择左兄弟,选择右兄弟也可以)结点合并,合并后的指向当前结点的指针就指向了父结点。
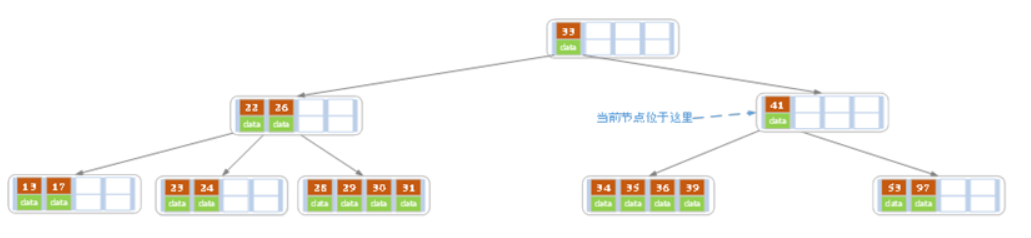
同理,对于当前结点而言只能继续合并了,最后结果如下所示。

合并后结点当前结点满足条件,删除结束。
B+树定义
B+树是B树的一种变形形式,B+树上的叶子结点存储关键字以及相应记录的地址,叶子结点以上各层作为索引使用。一棵m阶的B+树定义如下:
(1)每个结点至多有m个子女;
(2)除根结点外,每个结点至少有[m/2]个子女,根结点至少有两个子女;
(3)有k个子女的结点必有k个关键字。
B+树的查找与B树不同,当索引部分某个结点的关键字与所查的关键字相等时,并不停止查找,应继续沿着这个关键字左边的指针向下,一直查到该关键字所在的叶子结点为止。
B+树解决问题
同时支持随即检索与顺序检索
1.6 散列查找
哈希表的设计主要涉及哪几个内容?
- 哈希表节点定义
template<class Value>
struct hashtable_node{
hashtable_node *next;
Value val;
};
- 哈希表的定义
template<class Key, class Value>
class hashtable{
public:
//哈希表节点键值类型
typedef pair<Key, Value> T;
//表节点
typedef hashtable_node<T> node;
public:
//构造函数
hashtable();
hashtable(hashtable<Key, Value> &ht)
: buckets(ht.buckets), num_elements(ht.num_elements)
{}
//插入一个关键字
void insert(T kv);
//根据键值删除关键字
void erase(Key key);
//判断关键字是否在哈希表中
bool find(Key key);
//返回哈希表中关键字个数
int size(){
return num_elements;
}
void printHashTable();
private:
//根据传入大小判断是否需要重新分配哈希表
void resize(int num_elements);
//根据键值返回桶的编号
int buckets_index(Key key, int size){
return hash(key) % size;
}
//根据节点返回键值
Key get_key(T node){
return node.first;
}
private:
//使用STL list<T>作桶
vector<node*> buckets;
//哈希表中元素个数
size_t num_elements;
//哈希函数
hashFunc<Key> hash;
};
- 哈希函数的设计
/*
* 哈希函数的设定,只考虑 4 种键值类型的哈希函数
* char, int , double , string
*/
template<class Key> struct hashFunc{};
template<> struct hashFunc < char > {
size_t operator()(char x) const { return x; }
};
template<> struct hashFunc < int > {
size_t operator()(int x) const { return x; }
};
template<> struct hashFunc < double > {
size_t operator()(const double & dValue) const
{
int e = 0;
double tmp = dValue;
if (dValue<0)
{
tmp = -dValue;
}
e = ceil(log(dValue));
return size_t((INT64_MAX + 1.0) * tmp * exp(-e));
}
};
template<> struct hashFunc < string > {
size_t operator()(const string & str) const
{
size_t h = 0; for (size_t i = 0; i<str.length(); ++i)
{
h = (h << 5) - h + str[i];
}
return h;
}
};
哈希表

mod=13
- ASL成功=(18+21+4*1)/10=1.4
- ASL不成功=(2+1+1+9+8+7+6+5+4+3+2+1+3)/13=4.692
哈希链
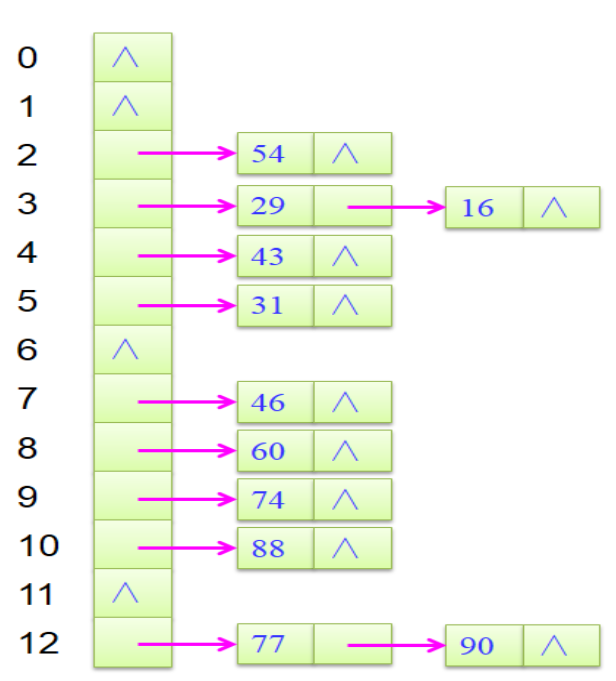
- ASL成功=(19+22)/11=1.182
- ASL不成功=(17+22)/13=0.846
2.PTA题目介绍(0--5分)
介绍3题PTA题目
2.1 是否完全二叉搜索树(2分)
2.1.1 伪代码(贴代码,本题0分)
将数据插入空的二叉搜索树
if <树为空>
建立新的节点
并对节点赋值为num
令左右孩子均为null
else if <num大于节点数据>
插入左孩子中
else if<num小于节点数据>
插入右孩子中
层次遍历输出结果树的层序遍历结果
判断该树是否为完全二叉树
if <树为空>
不是
令p为最后入队的元素
while(p)
{
p出列
p的左右孩子入列
令p为队头元素
}
当p为空时,弹出
while 队列不为空
{
if<队头元素不为空>
{
不是
}
弹出队列
}
是
}
2.1.2 提交列表

2.1.3 本题知识点
- 树的层次遍历
- 队列的相关库函数,如
①判断队列是否为空qu.empty()
②返回队列中第一个元素,即最后插入到队列中的那个元素qu.front()
③移除队首元素qu.pop()
④插入一个新元素在队尾qu.push(i)
⑤常用的库函数还有:返回队列中元素个数qu.size();返回队列中最后一个元素,即最先入队的那个元素qu.back();插入一个新的元素在队尾qu.emplace(i);交换q1,q1两个队列的内容q1.swap(q2)
2.2 航空公司VIP客户查询(2分)
2.2.1 伪代码(贴代码,本题0分)
定义数组
输入行数n与最低里程数k
for i++:0->n
{
输入会员身份证号码a及飞行里程b
if<飞行里程小于k>
按k计算
if<身份证号码曾出现过>
叠加b
else if<未出现过>
里程直接为b
}
输入查询者个数
for i++:0->M
{
输入查询者信息
if<信息存在>
输出飞行里程数
else
输出“No Info”
}
2.2.2 提交列表

2.2.3 本题知识点
- 一维数组的运用:用s[i]存储会员的身份证号码信息,用a[i]存储会员的累积飞行里程数
- for循环:通过循环来输入所需数据
2.3 基于词频的文件相似度(1分)
本题设计一个倒排索引表结构实现(参考课件)。单词作为关键字。本题可结合多个stl容器编程实现,如map容器做关键字保存。每个单词对应的文档列表可以结合vector容器、list容器实现。
2.3.1 伪代码(贴代码,本题0分)
输入文件总数N
for i++:1->N
{
while<未读到#>
for j++:0->文本长度
{
if<不是字母>
if<单词长度小于3>
不记录,重新循环
}
if<单词长度大于10>
只记录前十
else//单词长度在3到10之间
正常记录
将单词存入二维数组
单词长度归0
if<是字母>
把所有大写改为小写
}
最后一个字母需要单独判断,根据上方单词长度,以3,10为界,做不同情况讨论
输入查询个数
for i++:0->M
{
输入需查询的两文件序号
设置两个迭代器
for (同时对两个文件遍历)
it1和it2哪个字母小就让哪个向后移动
若相等,则
相同单词数++,it1,it2后移
}
输出结果
2.3.2 提交列表
2.3.3 本题知识点
- map函数:自动建立key - value的对应,map对象是模板类,需要关键字和存储对象两个模板参数:
std:map<int, string> personnel;
这样就可以定义一个用int作为索引,并拥有相关联的指向string的指针. - 一些常见的map函数操作:
-
begin():返回指向map头部的迭代器
-
clear():删除所有元素
-
count():返回指定元素出现的次数
-
empty():如果map为空则返回true
-
end():返回指向map末尾的迭代器
-
equal_range():返回特殊条目的迭代器对
-
erase():删除一个元素
-
find():查找一个元素
-
get_allocator():返回map的配置器
-
insert():插入元素
-
key_comp():返回比较元素key的函数
-
lower_bound():返回键值>=给定元素的第一个位置
-
max_size():返回可以容纳的最大元素个数
-
rbegin():返回一个指向map尾部的逆向迭代器
-
rend():返回一个指向map头部的逆向迭代器
-
size():返回map中元素的个数
-
swap():交换两个map
-
upper_bound():返回键值>给定元素的第一个位置
-
value_comp():返回比较元素value的函数
-

