神经网络优化算法

以下内容来自深度学习花树和维基百科

动量法

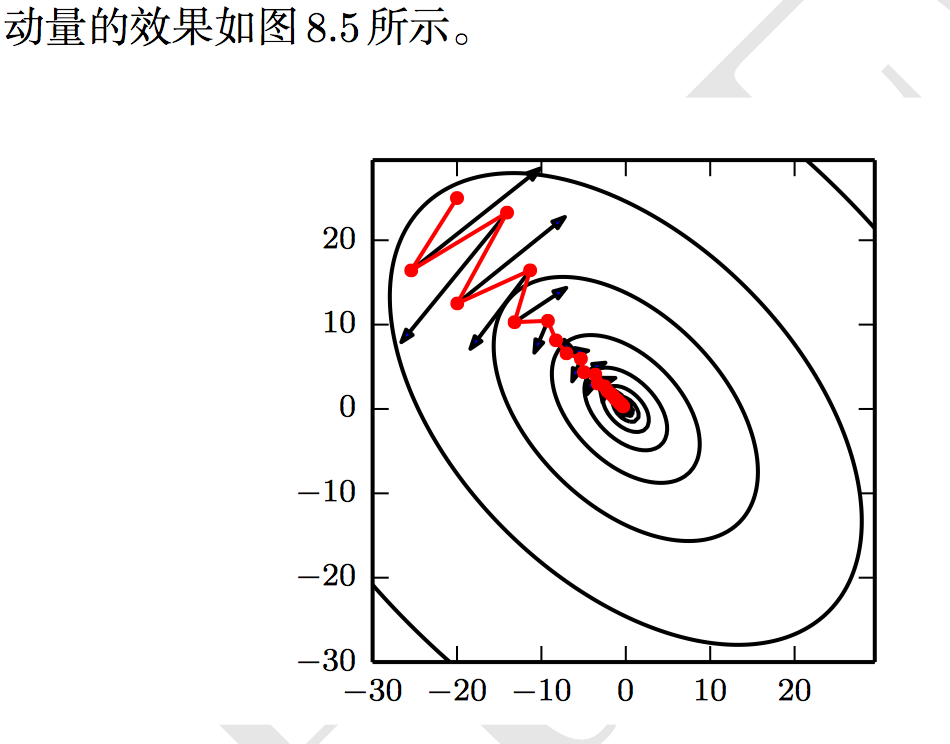
虽然随机梯度下降仍然是非常受欢迎的优化方法， 但其学习过程有时会很慢。 动量方法 (Polyak, 1964) 旨在加速学习，特别是处理高曲率、小但一致的梯度，或是带噪声的梯度。动量算法积累了之前梯度指数级衰减的移动平均，并且继续沿该方向移动。动量的效果如图 8.5 所示。





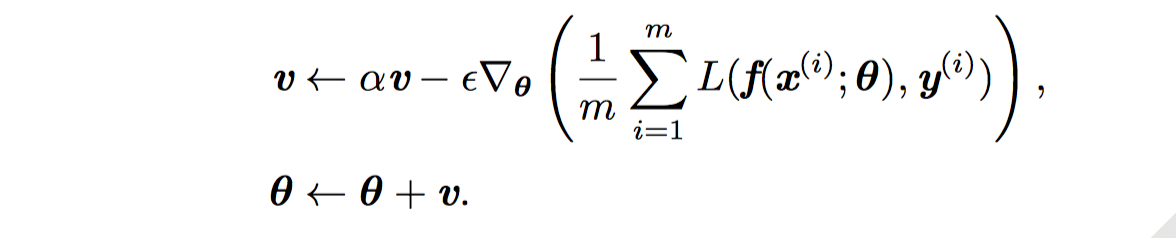
\[\begin{align*} v_0 &= 0 \\ v_1 &= \alpha \cdot 0 - \epsilon \cdot g \\ v_2 &= \alpha \cdot v_1 - \epsilon \cdot g = - \epsilon \space g \cdot (\alpha + 1) \\ v_3 &= \alpha \cdot v_2 - \epsilon \cdot g = - \epsilon \space g \cdot ({\alpha}^2 + \alpha + 1) \\ \vdots \\ v_n &= \alpha \cdot v_{n-1} - \epsilon \cdot g = - \epsilon \space g \cdot ({\alpha}^{n-1} + {\alpha}^{n-2}+ \cdots + {\alpha}^2 + \alpha +1) \\ &= - \epsilon \space g\left ( \frac{1-a^n}{1-a} \right) \\ &\approx \frac{ - \epsilon \space g}{1-a} \\ \end{align*} \]



Nesterov Momentum



AdaGrad



RMSProp





Adam