解 Ax = 0
已知: 已知 \(A \in R^{m\times n}, m \ge n\)
问题: \(Ax = 0\) 的解
求解: 解为A的右奇异矩阵V的最后一列, 即 \(A^TA\) 最小特征值对应的特征向量
基础知识
实对称矩阵
实对称矩阵: \(A = A^T, A \in R^{n\times n}\)
性质:
- 实对称矩阵A的不同特征值对应的特征向量是正交的。
- 实对称矩阵A的特征值都是实数,特征向量都是实向量。
- n阶实对称矩阵A必可相似对角化,且相似对角阵上的元素即为矩阵本身特征值。
由以上可知, \(A^TA\) 为实对称矩阵
正交矩阵
\(\square\) 正交矩阵Q是一个方阵,其元素为实数,而且行与列皆为正交的单位向量,使得该矩阵的转置矩阵为其逆矩阵:
\[{\displaystyle Q^{T}=Q^{-1}\Leftrightarrow Q^{T}Q=QQ^{T}=I.\,\!}
\]
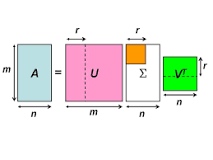
奇异值分解
A = \(U \Sigma V^T, \Sigma 为对角矩阵, U,V 分别为正交矩阵\)
式中 \(\Sigma = \begin{bmatrix} \Sigma_1 & O \\ O & O \end{bmatrix}\), 且 \(\Sigma_1=diag(\sigma1,\sigma2, ..., \sigma_r)\), 其对角线按照顺序
\[\sigma1\ge \sigma2 \ge\sigma_r>0, \quad
r = \bf Rank(A)\]
排列.
数值 \(\sigma1,\sigma2, ..., \sigma_r\) 连同 \(\sigma_{r+1} =\sigma_{r+1}=\cdots=\sigma_n=0\) 一起称为矩阵A的奇异值
\[A[v_1,\cdots,v_r,\cdots,v_n] = [u_1, \cdots,u_r,\cdots,u_m]\begin{bmatrix}\sigma_1\\&\ddots\\&&\sigma_r\\&&&0 \\ &&&&\ddots \\&&&&&0\end{bmatrix} \\
AV = U \Sigma \Rightarrow A = U\Sigma V^{-1} = U\Sigma V^T \\
A^TA = ( U\Sigma V^T)^T U\Sigma V^T = V\Sigma ^2V^T \\
AA^T = U\Sigma V^T( U\Sigma V^T)^T = U\Sigma ^2U^T \\
\]
解答
V 为正交矩阵, \(AV = U \Sigma\), 列向量形式为
\[Av_i=\begin{cases} \sigma_iu_i, \quad &i=1,2,3,\cdots,r \\
0, \quad \quad &i=r+1,r+2,\cdots,n
\end{cases}
\]
从上奇异值分解列向量形式可以看出, 取最小特征值对应的特征向量即为Ax=0的近似解
\(Ax = 0 \cong A^TAx = A^T0 = 0\)
solution 2
\(T = |Ax|_2, 约束|x|_2 = 1\)
\[T= |Ax|_2 = (Ax)^T(Ax = x^TA^TAx =x^T(A^TAx)= x^T(\sigma_i^2 x)) = \sigma_i^2 x^Tx =\sigma_i^2|x|_2 = \sigma_i^2
\]
其中 \(\sigma_i\) 为 \(A\) 的奇异值, \(x\) 为A的右奇异矩阵最小的奇异值对应的特征向量.



