单应矩阵
定义
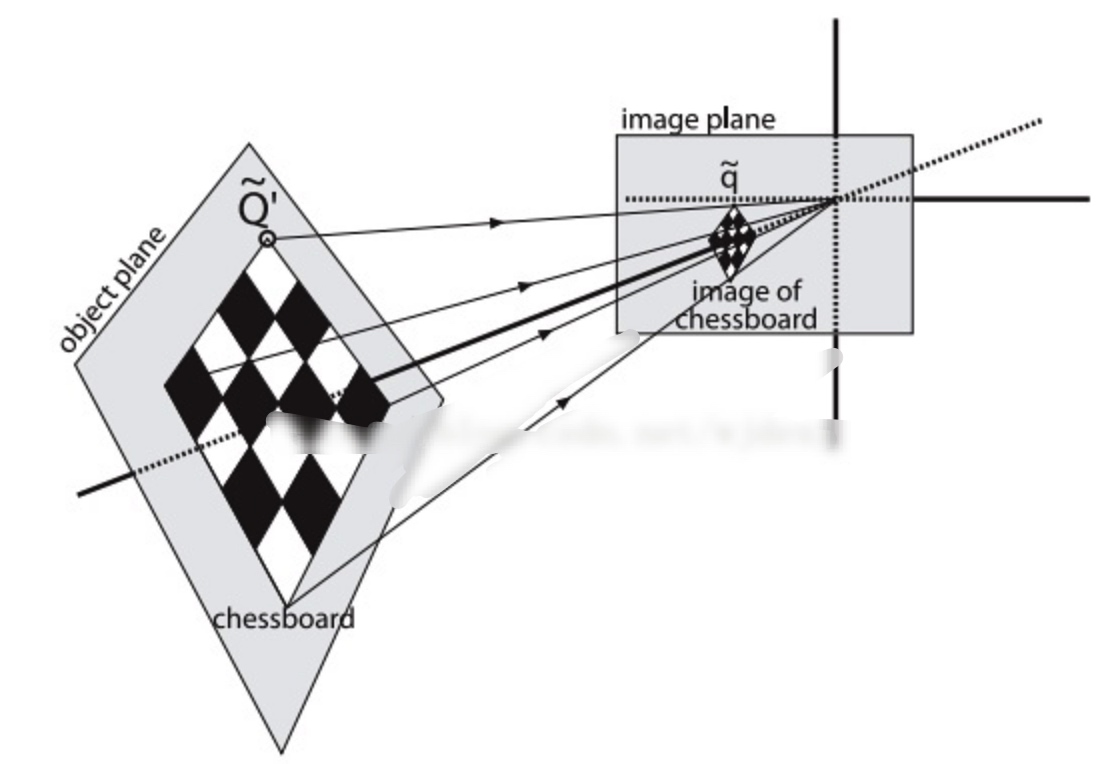
2D单应性变换定义为从一个平面到另一个平面的投影映射, 单应矩阵形式如下:
\[H= \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & h_{22} \end{bmatrix}
\]
坐标 \((x, y)\) 通过单应性变换映射到 \((u, v)\), 使用齐次坐标即为 \((x, y, 1)\), \((u, v, 1)\), 具有如下变换 \(\bf{x'=Hx}\)
\[s\begin{bmatrix}u\\v\\1\end{bmatrix}
= \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & h_{22} \end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}
\]
计算单应变换H需要多少对应点?
一方面矩阵H有9个参数, 但只确定到相差一个尺度因子s, 不妨约束 \(\|H\|\) = 1, 来避免h=0的解. 因此2D摄影变换的自由度是8,需要4个点对(任意3点不共线, 线性不相关)
直接线性变换(DLT)解法
齐次解
给予4个点对, 求齐次解
\[\begin{equation} \left\{ \begin{aligned} su&=h_{00}x + h_{01}y + h_{02}\\ sv&=h_{10}x + h_{11}y + h_{12}\\ s&=h_{20}x + h_{21}y + h_{22} \\ \end{aligned} \right. \end{equation}
\]
\[\begin{equation} \label{eq2} \begin{bmatrix} -x & -y &-1&0&0&0&xx_1&yx_1&x_1 \\ 0&0&0& -x & -y &-1&xy_1&yy_1&y_1 \\ \end{bmatrix} \begin{bmatrix}h_{00}\\h_{01}\\h_{02}\\h_{10}\\h_{11}\\h_{12}\\h_{20}\\h_{21}\end{bmatrix}=0 \end{equation} \\
Ah = 0
\]
矩阵 \(A \in \bf R^{8\times9}\), 最大可能秩为8, 那么齐次方程组有一个1维零空间, h的这样一个解只能在相差一个非零尺度因子下确定
超定解
如果给出的点对超过4, 矩阵 \(A \in \bf R^{m\times9, \space m>8}\)
如果点的位置精确的话, A的秩依然是8. 解法参上
如果图像测量点位置存在误差, 我们试图寻找一个近似解, 解为A的右奇异矩阵最小奇异值对应的特征向量, 解法详解
非齐次解
给予4个点对, 既然允许解相差任意一个尺度因子, 自然可以选择尺度因子值使得 \(h_j=1\), 不妨设 \(h_{22}=1\),
\[H= \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & 1 \end{bmatrix}
\]
即
\[s\begin{bmatrix}u\\v\\1\end{bmatrix}
= \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & 1 \end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}
\]
线性方程组如下:
\[\begin{equation} \left\{ \begin{aligned} su&=h_{00}x + h_{01}y + h_{02}\\ sv&=h_{10}x + h_{11}y + h_{12}\\ s&=h_{20}x + h_{21}y + 1 \\ \end{aligned} \right. \end{equation}
\]
化简可得
\[\begin{equation}
\begin{bmatrix}x & y &1&0&0&0&-xu&-yu \\ 0&0&0& x & y &1&-xv&-yv \\ \end{bmatrix} \begin{bmatrix}h_{00}\\h_{01}\\h_{02}\\h_{h10}\\h_{11}\\h_{12}\\h_{20}\\h_{21}\end{bmatrix} = \begin{bmatrix}u\\v\end{bmatrix} \end{equation} \\
Ah = b\\
h = A^{-1}b
\]
但是, 如果事实上真正解 \(h_j=0\), 那么不存在 \(kh_j=1\), 意味着令 \(h_j=1\) 得不到真正的解, 那么如果被选的\(h_j\)真正解接近于0, 该方法将导致不稳定解.
