Flexible Camera Calibration By Viewing a Plane From Unknown Orientations

URL: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/11/zhan99.pdf

简介

张正友标定法

论文提出一种灵活的新技术来轻松校准相机。 它仅需要照相机观察几个（至少两个）不同方向显示的平面图案。 相机或平面图案均可自由移动。 不需要知道运动。 径向透镜畸变被建模。 所提出的过程包括一个解析解的解决方案，然后是基于最大似然准则的非线性修正。 计算机仿真和实际数据都已用于测试该技术，并获得了很好的结果。 与使用昂贵的设备（例如两个或三个正交平面）的经典技术相比，该技术易于使用且灵活。 它使3D计算机视觉从实验室环境向现实世界的使用迈出了一步。

Algorithm

Notation

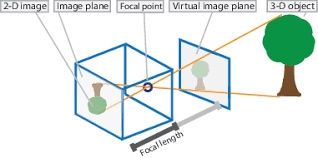
像素坐标系坐标 \(m = [u, v]^T\). 世界坐标系下坐标 \(M = [X, Y, Z]^T\), 使用 \(\tilde{x}\) 表示齐次坐标. \(\tilde{m} = [u, v, 1]^T, \space \tilde{M} = [X, Y, Z, 1]^T\)

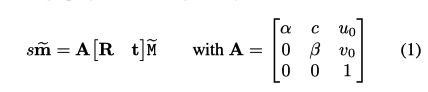
\(A\) 为相机内参, \([R|t]\) 为相机外参, 设标定板的\(Z=0\), 有

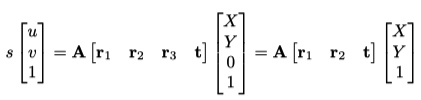
模型平面与其图像之间的单应性矩阵

单应性: 定义为从一个平面到另一个平面的投影映射
由于标定板上 \(Z=0\), 令 $ \tilde{M} = [X, Y, 1]^T$

可以根据给定模型平面的图片估计单应性矩阵(见后面), 设单应性矩阵 \(H = [h_1, h_2, h_3]\), 有

其中, λ是任意标量。

\(r_1, r_2\)为外参旋转矩阵R(正交矩阵)的列向量, 满足如下约束:

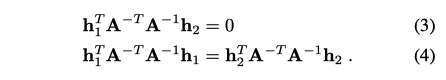
Solving Camera Calibration

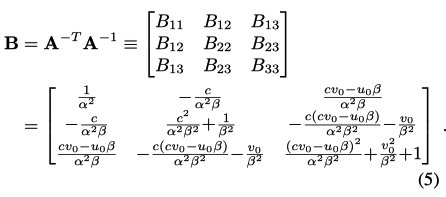
设 H \(i^{th}\) 列向量表示为 \(h_i = [h_{i1}, h_{i2}, h_{i3}]^T\)

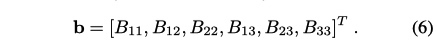
则

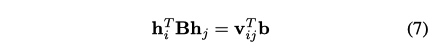
将 \(h^T_iBh_j\) 展开, 可知 \(v_{ij}\) 为

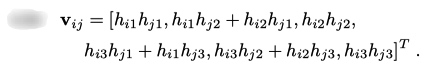
由(3)(4) 可知

关于式(9)解法参照 Ax =0

一旦得到了b, 那么可得内参A

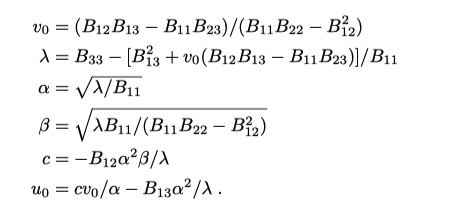
外参

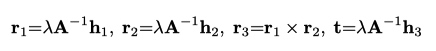
其中,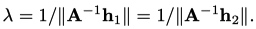

关于切向畸变的非线性估计方法详见论文

Estimation of the Homography Between the Model Plane and its Image

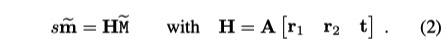
理想情况下，模型平面上点M和像素坐标m应该满足式(2). 实际上，并不能满足, 因为提取的图像点中存在噪声. 假设\(m_i\)上噪声为服从均值为0和协方差矩阵为\(Λ_{mi}\)的高斯噪声。 单应矩阵可以最大似然估计最小化如下函数

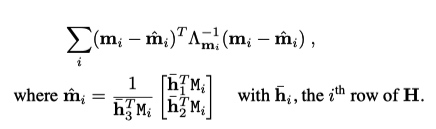
这里\(\hat{h}_i\) 也是采用列向量表示法

假设 \(\space \forall i, \space \Lambda_{m_i} = \sigma^2I\), 那么上述问题等价于非线性最小二乘问题. 即 \(\sum_i||m_i - \hat{m_i}||^2\). 可以通过Levenberg-Marquardt Algorithm 来优化, 优化算法的初值可以通过如下方案获得.

令\(H = x = [\bar{h1}^T_1, \bar{h}^T_2, \bar{h}^T_3]\)

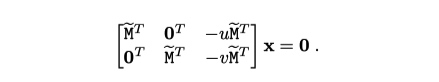
如上表达式为将 HM = m 展开后所得

Experiment Detail