Large-Margin Softmax Loss for Convolutional Neural Networks

L-Sofmax

paper url: https://arxiv.org/pdf/1612.02295
year:2017

Introduction

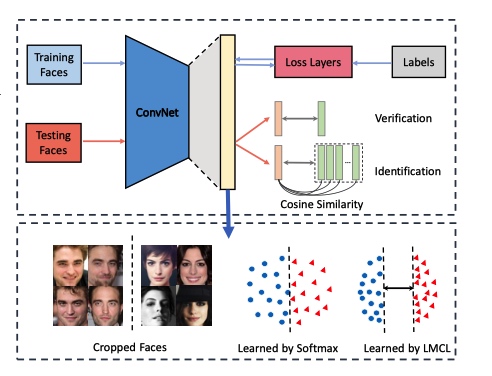
交叉熵损失与softmax一起使用可以说是CNN中最常用的监督组件之一。 尽管该组件简单而且性能出色, 但是它只要求特征的可分性, 没有明确鼓励网络学习到的特征具有类内方差小, 类间方差大的特性。 该文中，作者提出了一个广义的 large margin softmax loss(L-Softmax)，是large margin系列的开篇之作. 它明确地鼓励了学习特征之间的类内紧凑性和类间可分离性。

Softmax Loss

Softmax Loss定义如下

\[\bf \text{Softmax Loss = FC + Softmax + Cross-Entropy} \]



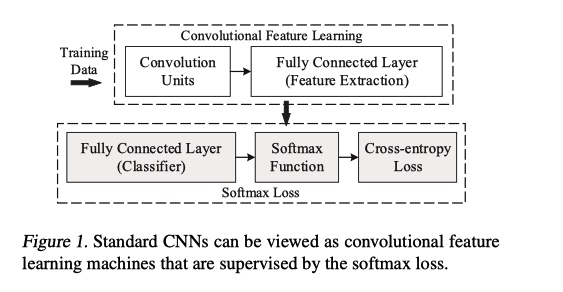
如上图, 当前CNN分类网络可以看成 特征提取backbone+Softmax Loss 部分
特征提取网络最后一层特征记为 \(\bf x\), 最后一层 FC 可以看成一个 N 类线性分类器, N 为类别数.

Insight

由于 Softmax 并没有明确地鼓励类内紧凑性和类间分离性。 基于此, 该文中一个insight就是, 特征提取网络提取的特征向量 x 和与相应类别c的权重向量\(W_c\)的乘积可以分解为模长+余弦值:

\[W_cx = ||W_c||_2 ||x||_2 \cos(θ_c) \]

其中, c为类别索引， \(W_c\) 是最后一个FC层的参数, 可以认为是的类别 c 的线性分类器。

从而, L-Softmax 重构如下


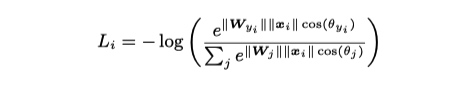
这样, 在L-Softmax loss中，类别预测很大程度上取决于特征向量\(x\)与权重\(W_c\)的余弦相似性.

method

余弦函数如下


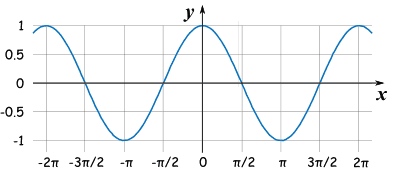
当 \(\theta = [0, \pi]\)时候, \(\cos(\theta)\) 单调递减

下面以二分类为例, 对于类别 1

Softmax 要求,

\[W_1x > W_2x \\ \Downarrow \\ ||W_1||_2 ||x||_2 \cos(θ_1) > ||W_2||_2 ||x||_2 \cos(θ_2) \\ \Downarrow \\ ||W_1||_2 \cos(θ_1) > ||W_2||_2 \cos(θ_2) \\ \]

L-Softmax 要求,

\[||W_1||_2 \cos(mθ_1) > ||W_2||_2 \cos(θ_2) \]

那么, 由于\(\cos\theta\) 在 \([0, \pi]\)上的单调递减特性, 有如下不等式

\[||W_1||_2 \cos(θ_1) \gt ||W_1||_2 \cos(mθ_1) > ||W_2||_2 \cos(θ_2), \quad m \gt 1 \]

定义



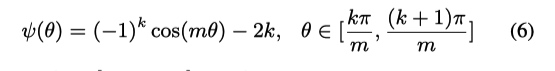
几何上直观理解如下



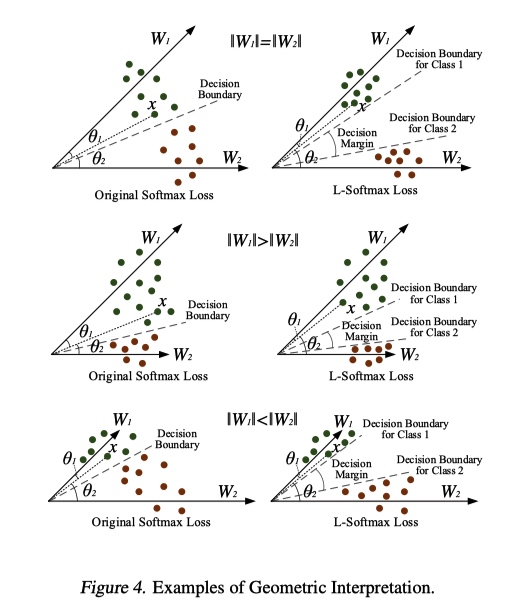
property

L-Softmax损失具有清晰的几何解释. m控制类别之间的差距. 随着m越大(在相同的训练损失下)，类之间的margin变得越大, 学习困难也越来越大.
L-Softmax损失定义了一个相对困难的学习目标，可调节margin(margin 表示了特征学习困难程度)。 一个困难的学习目标可以有效地避免overfiting，并充分利用来自深层和广泛架构的强大学习能力。

experiment result

toy example





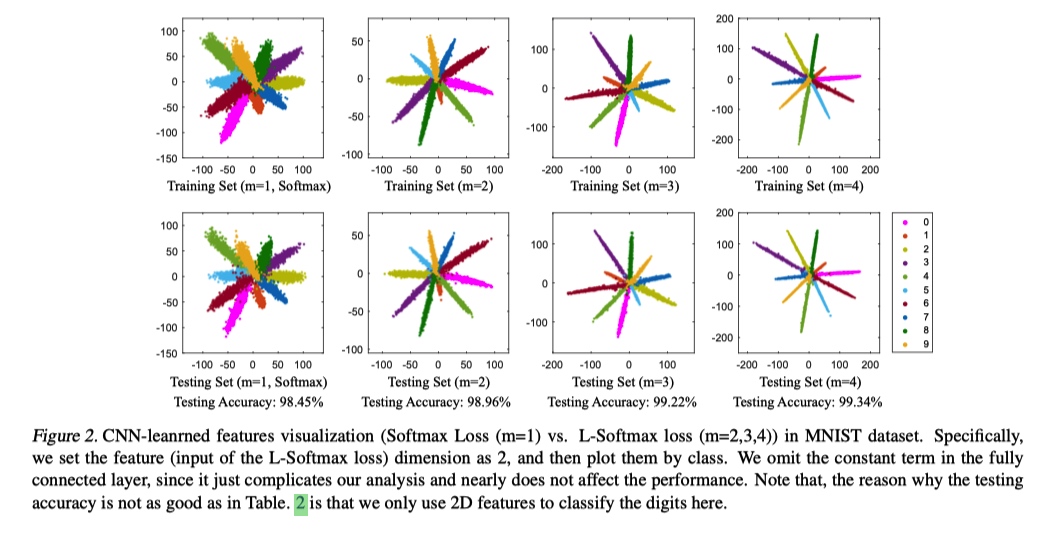
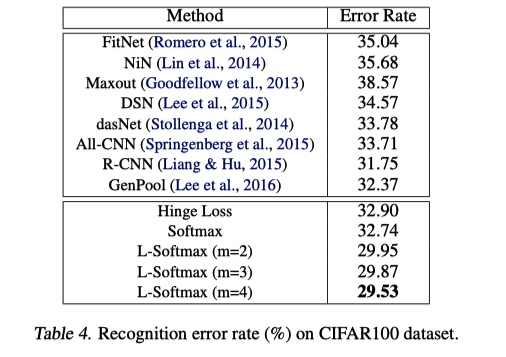
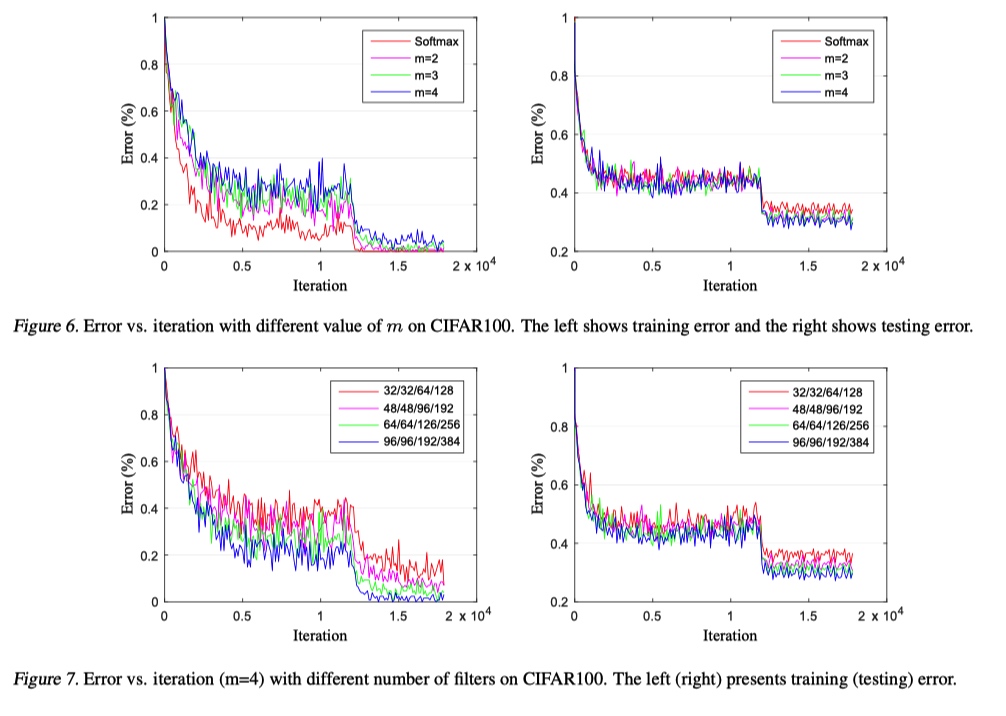
可以看出, L-softmax 的训练损失更大, 但是在测试集上损失更小.

thought

该篇论文为 larger-margin softmax loss 的开篇之作. 提出乘性 larger-margin softmax loss, 相较与加性 larger-margin softmax loss(如 AM-softmax, ArcFace), 训练难度更大(需要用到退火训练方法, 见原文 5.1), 效果而言, 也是加性 loss 更好.

从

\[||W_1||_2 \cos(θ_1) \ge ||W_1||_2 \cos(mθ_1) > ||W_2||_2 \cos(θ_2), \quad m \ge 1 \]

可以看出, 该不等式不仅依赖余弦角度而且依赖最后一层 FC 的权重的模长, 所以, 为了学习的特征更加专注于对于余弦角度的优化, 后面一批论文很多都用到权重归一化, 效果很好.

同时可以看到, 在特征分类时, 其实 feature 的模长会被消元, 为了各个类别学习的特征更加有判别能力, 后面一批论文也做了特征归一化(实际上将特征模长限制为 1 会降低特征的表达能力, 其实在加难特征学习的过程)

总之, 后面的各个large margin 系列, 特征归一化, 权重归一化已经是标配了.

A-Softmax

paper: SphereFace: Deep Hypersphere Embedding for Face Recognition
url: http://openaccess.thecvf.com/content_cvpr_2017/papers/Liu_SphereFace_Deep_Hypersphere_CVPR_2017_paper.pdf
year: 2017

相较于 L-Softmax, A-Softmax 将最后一层 FC 的权重进行了归一化处理, 即 \(||W||=1\), 重构后 A-Softmax 形式如下



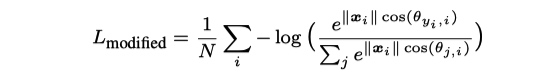
Weight Normlized Softmax

同样以二分类为例, 对于类别 1, 有

\[W_1x > W_2x \\ \Downarrow \\ ||W_1||_2 ||x||_2 \cos(θ_1) > ||W_2||_2 ||x||_2 \cos(θ_2) \\ \Downarrow \\ ||W_1||_2 \cos(θ_1) > ||W_2||_2 \cos(θ_2) \\ \Downarrow \\ \cos(θ_1) > \cos(θ_2) \]

A-Softmax, 有

\[ \cos(mθ_1) > \cos(θ_2) \]

CosFace

paper: CosFace: Large Margin Cosine Loss for Deep Face Recognition
url: https://arxiv.org/abs/1801.09414
year: 2018



这篇论文在权重归一化的基础上进行了特征归一化, 固定\(||x||=s\)
权重和特征归一化后, Softmax 形式如下



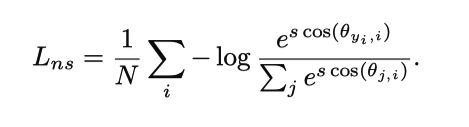
feature normalization

训练时, 给定特征向量 \(x\)，令 \(\cos(θ_i)\)和\(\cosθ_j\)分别表示两个类的余弦值。
如果没有对特征进行归一化(已经进行权重归一化)，则LMCL强制

\[\|x\|_2\cos(θ_i) \gt \|x\|_2 \cosθ_j \]

注意，只要要\(\cos(θ_i) < \cos(θ_j)\)，就需要降低 \(\|x\|_2\)以使损失最小化, 这导致优化退化问题. 因此，在LMCL的监督下，特征归一化至关重要，尤其是当网络从头开始训练时。 同样地，固定缩放参数s好于自适应学习s。

details

以二分类为例, 对于类别 1,

\[loss_{ce} = -\ln\frac{e^{|x|\cos\theta_1}}{e^{|x|\cos\theta_1} + e^{|x|\cos\theta_2}} \\ 令 \quad p = e^{\cos\theta_1}, q = e^{\cos\theta_2}, \quad \\ \cos\theta_1, \cos\theta_2 \in [0, 1] \rightarrow p, q \in [1, e] \\ loss_{ce} = -\ln\frac{p^{|x|}}{p^{|x|} + q^{|x|}} \\ 令 f(x) = \frac{p^{x}}{p^{x} + q^{x}}, x>0 \\ f^{\prime}(x) = \frac{(pq)^{x}}{(p^{x} + q^{x})^2}\ln{\frac{p}{q}} \\ \]

当 p>q 时, 分类正确, f(x)为增函数, loss(x) 为减函数, 故而为了减小 loss(x), x增加, 没有专注于优化余弦角度

当 p<q 时, 分类错误 , f(x)为减函数, loss(x) 为增函数, 故而为了减小 loss(x), x减小, 没有专注于优化余弦角度

Large Margin Cosine Loss(LMCL)

以二分类为例, 对于类别 1, CosFace有

\[\cos(θ_1) > \cos(θ_1) - m > \cos(θ_2) \]

Large Margin Cosine Loss(LMCL) 形式如下


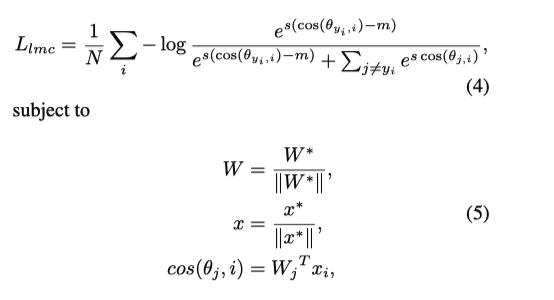
这里将把特征和权重归一化的, 而不加入 margin 的 Softmax Loss 定义为 NSL(Normlized Softmax Loss)

下面总结下上述几种 loss 的决策边界(decision margin),


loss \(\quad \quad\quad\quad\)	decision margin	details
Softmax	$ | W_1|_2  \cos(θ_1) > |W_2|_2 \cos(θ_2)$	其边界取决于权重向量的模长和余弦值，这导致余弦空间中的决策区域重叠(margin<0)。 人脸识别中, 测试阶段仅考虑测试面部特征向量之间的余弦相似性是一种常见策略。 因此, 受过Softmax损失的训练有素的分类器无法对余弦空间中的测试样本进行完美分类。
L-Softmax	$ | W_1|_2  \cos(mθ_1) > |W_2|_2 \cos(θ_2)$
NSL	$ \cos(θ_1) > \cos(θ_2) $	通过剔除模长变变量，NSL能够在余弦空间中对测试样本进行完美分类，margin为0.但是，它不是很稳定 因为没有decision margin抵消噪音的影响, 决策边界周围的任何小扰动都会改变决策。
A-Softmax	$ \cos(mθ_1) > \cos(θ_2) $	A-Softmax的边界在所有θ值上并不连续: 当θ减小时，margin变小，并且当θ=0时，margin完全消失。这导致两个潜在的问题。1. 对于视觉上相似的特征, 该特征与 \(W_1\) 和 \(W_2\) 之间都具有较小角度, 从而难以区分类别\(C_1\)和 \(C_2\)。 2，从技术上讲，人们必须采用额外的技巧和临时分段函数来克服余弦函数的非单调性问题。
LMCL	$ \cos(θ_1) - m > \cos(θ_2) $	上图中, 可以看到LMCL产生的明显margin \(\sqrt 2 m\)。 这表明LMCL比NSL更稳健，因为决策边界(虚线)周围的小扰动不太可能导致错误的决策. 无论其权重向量的角度如何，加性余弦 margin 都可以可以应用于所有样本。

experiment result

effect of margin config



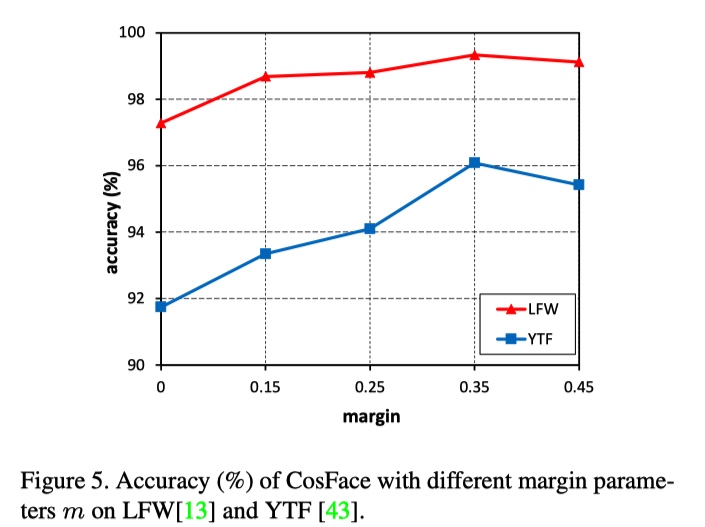
effect of feature normlization



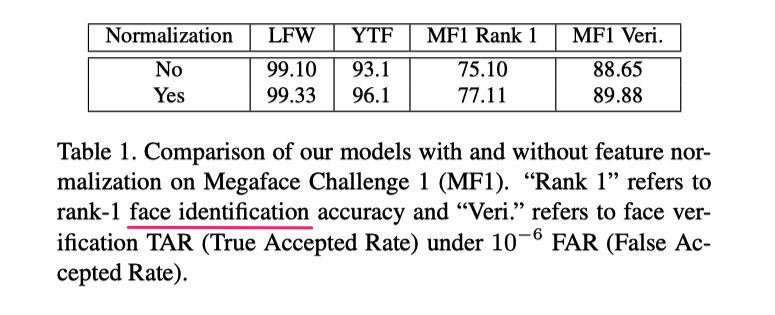
face recognition