Huber Loss
Huber Loss 是一个用于回归问题的带参损失函数, 优点是能增强平方误差损失函数(MSE, mean square error)对离群点的鲁棒性。
当预测偏差小于 δ 时，它采用平方误差,
当预测偏差大于 δ 时，采用的线性误差。
相比于最小二乘的线性回归，HuberLoss降低了对离群点的惩罚程度，所以 HuberLoss 是一种常用的鲁棒的回归损失函数。
Huber Loss 定义如下
\[\begin{split}
L_\delta(a)=\left \{
\begin{array}{ll}
\frac12a^2,&\textrm{for } |a|\leq\delta,\\
\delta\cdot(|a|-\frac12\delta),&\textrm{otherwise.}
\end{array}
\right.
\end{split}
\]

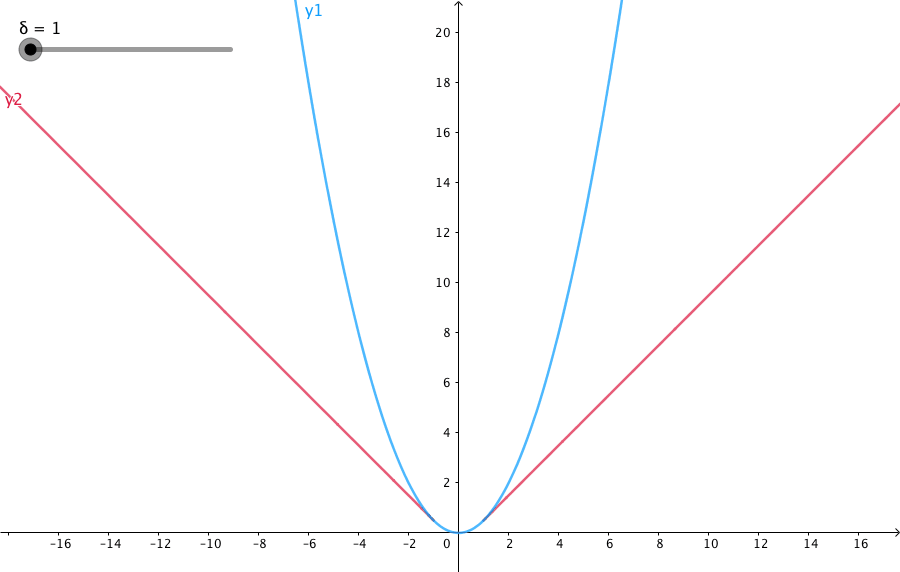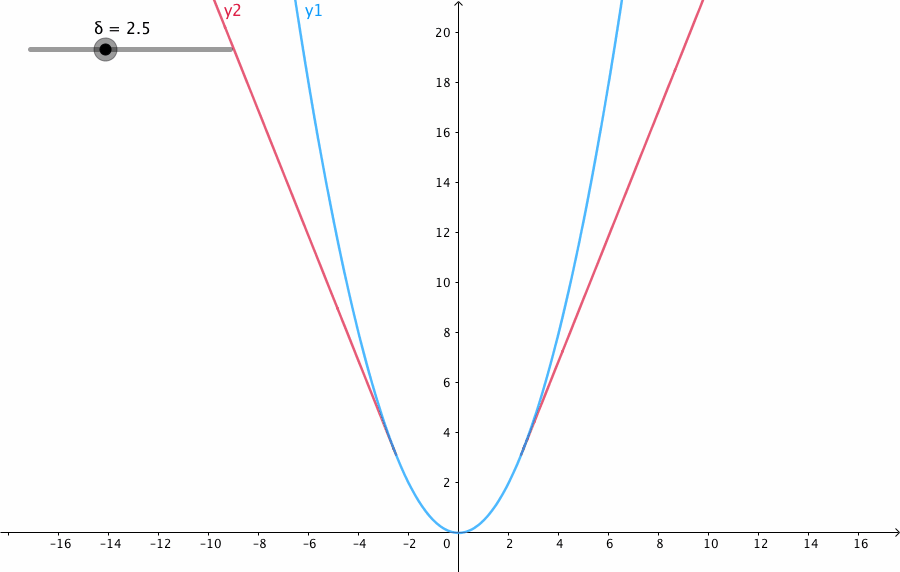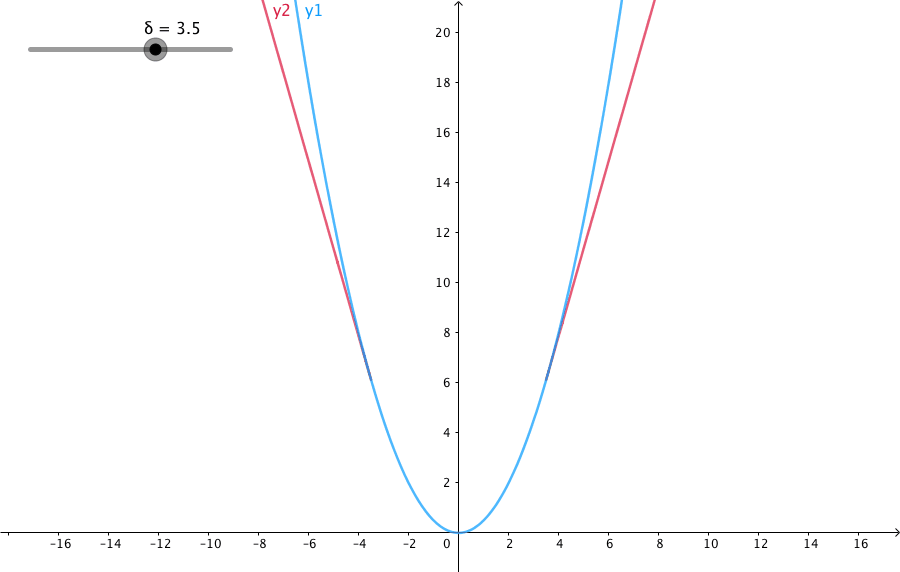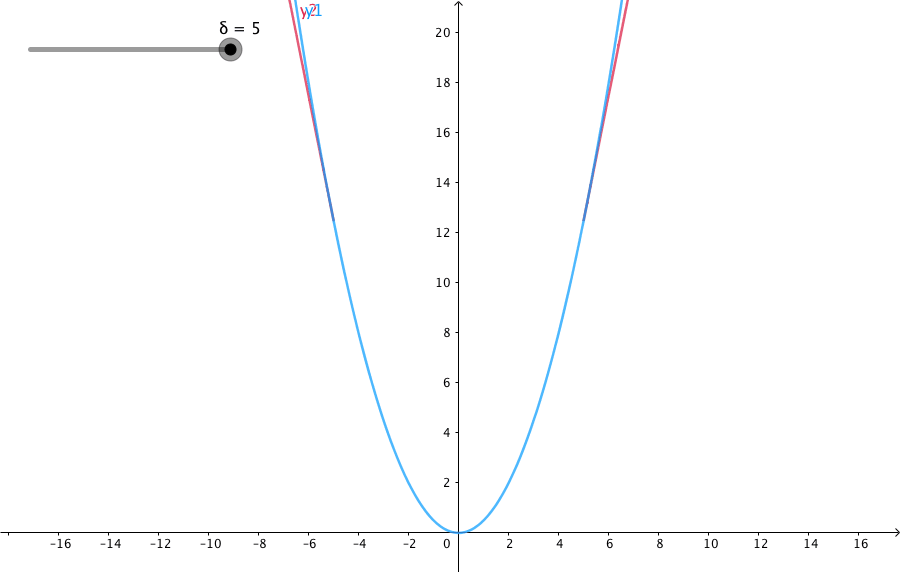
参数 a 通常表示 residuals，写作 y−f(x)，当 a = y−f(x) 时，Huber loss 定义为：
\[\begin{split}
L_\delta(y, f(x))=\left\{
\begin{array}{ll}
\frac12(y-f(x))^2,&\textrm{for }|y-f(x)|\leq\delta\\
\delta\cdot(|y-f(x)|-\frac12\delta),&\textrm{otherwise.}
\end{array}
\right.
\end{split}
\]
δ 是 HuberLoss 的参数，y是真实值，f(x)是模型的预测值, 且由定义可知 Huber Loss 处处可导
