Graham 扫描法找凸包(convexHull)

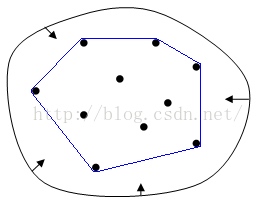
凸包定义

通俗的话来解释凸包：给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点



Graham扫描法

1. 由最底的一点 \(p_1\) 开始（如果有多个这样的点，那么选择最左边的），计算它跟其他各点的连线和 x 轴正向的角度，按小至大将这些点排序，称它们的对应点为 \(p_{2},p_{3},...,p_{n}\)。这里的时间复杂度可达 \(O(n \log {n})\)

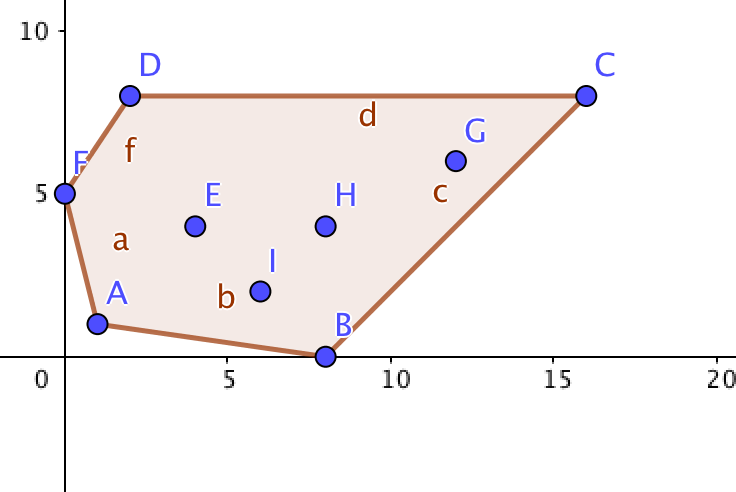
2. 以下图为例，基点为H，根据夹角由小至大排序后依次为H，K，C，D，L，F，G，E，I，B，A，J。下面进行逆时针扫描。


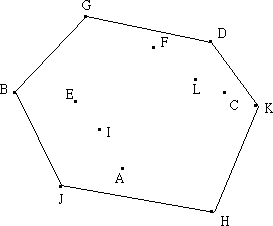
3. 线段<H, K>一定在凸包上，接着加入C。假设线段<K, C>也在凸包上，因为就H，K，C三点而言，它们的凸包就是由此三点所组成。但是接下来加入D时会发现，线段<K, D>才会在凸包上，所以将线段<K, C>排除，C点不在是凸包上。
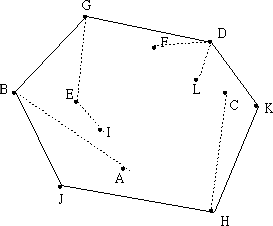
4. 即当加入一点时，必须考虑到前面的线段是否会出现在凸包上。从基点开始，凸包上每条相临的线段的旋转方向应该一致。如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断，设新加入的点为 \(p_{n + 1}\)，上一点为 \(p_n\)，再上一点为 \(p_{n - 1}\)。顺时针扫描时，如果向量 \(<p_{n - 1}, p_n>\) 与 \(<p_n, p_{n + 1}>\) 的叉积为正，则将上一点删除。
5. \(\color{red}{删除过程需要回溯，将之前所有叉积符号相反的点都删除，然后将新点加入凸包。}\)


Graham扫描法主要用一个\(\color{red}{栈}\)来解决凸包问题，点集 Q 中每个点都会进栈一次，不符合条件的点会被弹出，算法终止时，栈中的点就是凸包的顶点(逆时针顺序在边界上)。该算法具体步骤为



由于选择第一个基点时, 选择的是 y 坐标最小且最靠左的点, 所以极角取值范围 [0, 180), 我们关心的是极角的相对大小, 而不用求角度具体大小(虽然可以通过 \(\cos(\theta)\) 在 [0, 180)递减性质 来求实际角度大小), 所以极角排序可以通过向量叉积来做. 如果 \(p_1 \times p_2\) 向量叉积为正, 则 \(p_2\) 在 \(p_1\) 逆时针放心, 那么 \(p_2\) 与 x 正方向夹角比 \(p_1\) 大

旋转方向

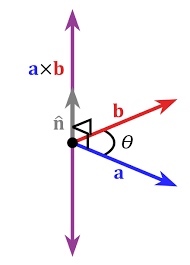
叉积

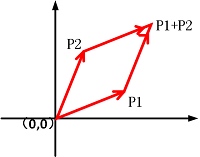
有向量 \(p1\) 和 \(p2\), 我们可以把叉积理解为由点 \((0,0)\)， \(\vec p_1\)， \(\vec p_2\) 和 \(\vec p_1+ \vec p_2\) 所构成的平行四边形有向面积.



二维平面点叉乘行列式：

\[\vec p_1 \times \vec p_2 = \begin{bmatrix} \vec i & \vec j & \vec k \\ a_x & a_y & 0\\ b_x & b_y & 0\\ \end{bmatrix} = (a_xb_y-a_yb_x)\space \vec k\]

相对坐标原点，若 \(\vec p_1 \times \vec p_2\)值为正，\(\vec p_2\) 在 \(\vec p_1\) 逆时针方向，若值为负，\(\vec p_2\) 在 \(\vec p_1\) 顺时针方向。相对公共端点 \(\vec p_0\)，叉积计算为

\[(\vec p_1 - \vec p_0) \times (\vec p_2 - \vec p_0) = (x_1 - x_0) \times (y_2 - y_0) - (x_2 - x_0) \times (y_1 - y_0) \]

一个简单的确定满足 “右手定则” 向量叉积的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从 \(\vec a\) 以不超过 180 度的转角转向 \(\vec b\) 时，竖起的大拇指指向是 \(\vec c\) 的方向.



代码实现



#include <iostream>
#include <vector>
#include <climits>
#include <algorithm>
#include <stack>
using namespace std;

template <typename T>
struct Point {
    T x;
    T y;
    Point(): x(0), y(0){};
    Point(T x_, T y_): x(x_), y(y_){};
};

bool isLeftTurn(Point<int> &p0, Point<int> &p1, Point<int> &p2) {
    return (p1.x - p0.x) * (p2.y - p0.y) >= (p1.y - p0.y) * (p2.x - p0.x);
}

int main() {
    vector<Point<int>> points;
    points.emplace_back(1, 1);
    points.emplace_back(8, 0);
    points.emplace_back(16, 8);
    points.emplace_back(2, 8);
    points.emplace_back(4, 4);
    points.emplace_back(0, 5);
    points.emplace_back(12, 6);
    points.emplace_back(8, 4);
    points.emplace_back(6, 2);

    // output: (8,0) (16,8) (2,8) (0,5) (1,1)
    if (points.empty()) {
        return 0;
    }
    int y_min = INT_MAX;
    int x_min = INT_MAX;
    int start_index = 0;
    for (int i = 0; i < points.size(); i++) {
        if (points[i].y < y_min) {
            y_min = points[i].y;
            x_min = points[i].x;
            start_index = i;
        } else if (points[i].y == y_min) {
            x_min = points[i].x;
            start_index = i;
        }
    }
    vector<Point<int>> st;
    st.emplace_back(0, 0);
    points.erase(points.begin()+start_index);
    for (auto &point : points) {
        point.x -= x_min;
        point.y -= y_min;
    }

    sort(points.begin(), points.end(), [](Point<int>& p1, Point<int>& p2) {
        if (p1.x * p2.y == p1.y * p2.x) {
            return p1.x * p1.x + p1.y * p1.y < p2.x * p2.x + p2.y * p2.y;
        }
        return p1.x * p2.y > p1.y * p2.x;
    });

    st.push_back(points[0]);
    for (int i = 1; i < points.size();) {
        if (isLeftTurn(st[st.size() - 2], st.back(), points[i])) {
            st.push_back(points[i]);
            i++;
        } else {
            st.pop_back();
        }
    }

    for (auto &i : st) {
        cout << i.x + x_min << '\t' << i.y + y_min << endl;
    }
    return 0;
}

 
 

参考: https://blog.csdn.net/u012328159/article/details/50808360