已知路面同一位置不同高度2点, 获取此两点坐标
已知相机内参以及与路面坐标系的之间的外参, 若已知路面同一位置不同高度2点A, B的图片坐标(u0, v0), (u1, v1), 求此两点世界坐标系下坐标, 不妨设A(x0, y0, z0), B(x0, y0, z1)

世界坐标系 => 相机坐标系
\[\begin{align*}
\begin{bmatrix}
x_c\\y_c\\z_c
\end{bmatrix}= \begin{bmatrix}
r_{00} & r_{01} & r_{02} & t_0 \\
r_{10} & r_{11} & r_{12} & t_1 \\
r_{20} & r_{21} & r_{22} & t_2 \\
\end{bmatrix}
\begin{bmatrix}
x_w\\y_w\\z_w \\1
\end{bmatrix}
\end{align*}
\]
相机坐标系 => 像素坐标系
\[\begin{align*}
s\begin{bmatrix}
u\\v\\1
\end{bmatrix} &=
\begin{bmatrix}
f_x & 0 & c_x \\
0 & f_y & c_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x_c\\y_c\\z_c
\end{bmatrix}
\end{align*}
\]
由如上可得
\[ \left\{ \begin{aligned}
\frac{r_{00}x_w + r_{01}y_w + r_{02}z_w + t_0}{r_{20}x_w + r_{21}y_w + r_{22}z_w + t_2} =\frac{x_c}{z_c} = \frac{u-c_x}{f_x} = a \\
\frac{r_{10}x_w + r_{11}y_w + r_{12}z_w + t_1}{r_{20}x_w + r_{21}y_w + r_{22}z_w + t_2} = \frac{y_c}{z_c} = \frac{v-c_y}{f_y} =b
\end{aligned}
\right.
\]
\[ \left\{ \begin{aligned}
(r_{00}-ar_{20})x_w + (r_{01}-ar_{21})y_w + (r_{02}-ar_{22})z_w = at_2 - t_0 \\
(r_{10}-br_{20})x_w + (r_{11}-br_{21})y_w + (r_{12}-br_{22})z_w = bt_2 - t_1
\end{aligned}
\right.
\]
令
\[ \left\{ \begin{aligned}
a_0 = \frac{u_0-c_x}{f_x} \\
b_0 = \frac{v_0-c_y}{f_y} \\
a_1 = \frac{u_1-c_x}{f_x} \\
b_1 = \frac{v_1-c_y}{f_y} \\
\end{aligned}
\right.
\]
则
\[ \left\{ \begin{aligned}
(r_{00}-a_0r_{20})x_0 + (r_{01}-a_0r_{21})y_0 + (r_{02}-a_0r_{22})z_0 + 0z_1 = a_0t_2 - t_0 \\
(r_{10}-b_0r_{20})x_0 + (r_{11}-b_0r_{21})y_0 + (r_{12}-b_0r_{22})z_0 + 0z_1 = b_0t_2 - t_1 \\
(r_{00}-a_1r_{20})x_0 + (r_{01}-a_1r_{21})y_0 + 0z_0 + (r_{02}-a_1r_{22})z_1 = a_1t_2 - t_0 \\
(r_{10}-b_1r_{20})x_0 + (r_{11}-b_1r_{21})y_0 + 0z_0 + (r_{12}-b_1r_{22})z_1 = b_1t_2 - t_1 \\
\end{aligned}
\right.
\]
则
\[\begin{bmatrix}
(r_{00}-a_0r_{20}) & (r_{01}-a_0r_{21}) & (r_{02}-a_0r_{22}) & 0 \\
(r_{10}-b_0r_{20}) & (r_{11}-b_0r_{21}) & (r_{12}-b_0r_{22}) & 0 \\
(r_{00}-a_1r_{20}) & (r_{01}-a_1r_{21})& 0 & (r_{02}-a_1r_{22})\\
(r_{10}-b_1r_{20}) & (r_{11}-b_1r_{21}) & 0 & (r_{12}-b_1r_{22})\\
\end{bmatrix} \begin{bmatrix}x_0 \\ y_0
\\z_0 \\z_1
\end{bmatrix}
= \begin{bmatrix}a_0t_2 - t_0 \\ b_0t_2 - t_1
\\a_1t_2 - t_0 \\b_1t_2 - t_1
\end{bmatrix}
\]
\[x=A^{-1}b
\]
问题反馈:上面的方案看起来合理, 可是列式计算时, 发现解法不正确. 记上述四元四次方程组为 Ax=b, 其中A有一个特征值特别小, 也就是说Det(A)的秩为3, 方程有无穷解. 猜测原因, 如下图, 已知P1, P2点坐标, 可以有无穷组同一位置不同高度的点组与之对应.
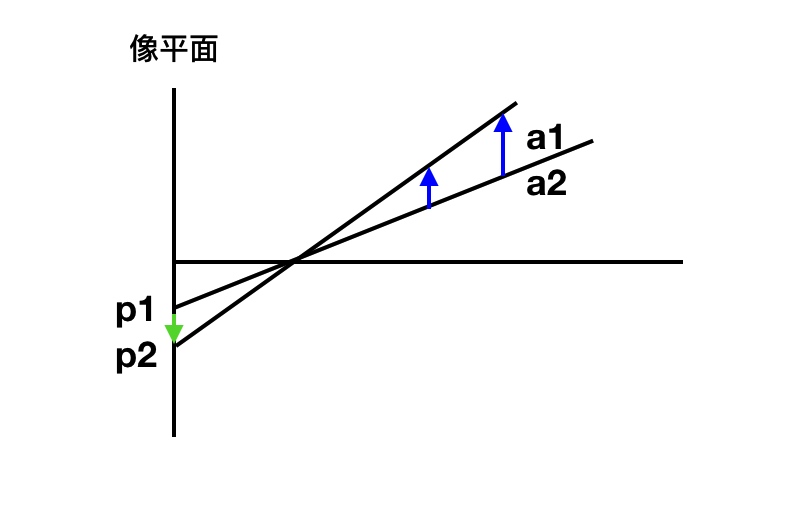
此时如果能知道a1, a2点实际的高度差, 那么该问题就变成了3元3次问题, 可解(已经验证)

