0/1 背包

有 N 件物品和一个容量为C的背包, 第i件物品的体积是 W[i]，价值是 V[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量，且价值总和最大。

解法 1

时间复杂度 \(O(n^2)\)
空间复杂度 \(O(n^2)\)

#include <iostream>
#include <vector>
using namespace std;
int main () {

    int capacity = 10;
    if (capacity <= 0) return 0;

    vector<int> volumes {3, 4, 5};
    vector<int> values {4, 5, 6};  // maxValue: 11
    size_t num = volumes.size();

    // volumes, values 开始索引从 0 到 1, 便于 for 循环中的对应和理解
    volumes.insert(volumes.begin(), 0);
    values.insert(values.begin(), 0);

    // maxValue[i][j]的含义: 将前 i 个物品中的一些物品装入容量为 j 的背包所能产生的最大价值
    vector<vector<int>> maxValue(num+1, vector<int>(capacity+1, 0));
    for (int i = 1; i <= num; i++) {
        for (int cap = 1; cap <= capacity; cap++) {
            if (volumes[i] > cap) {
                maxValue[i][cap] = maxValue[i-1][cap];
            } else {
                maxValue[i][cap] = max(maxValue[i-1][cap], maxValue[i-1][cap-volumes[i]]+values[i]);
            }
        }
    }
    cout << maxValue[num][capacity];
    return 0;
}

具体流程如下:



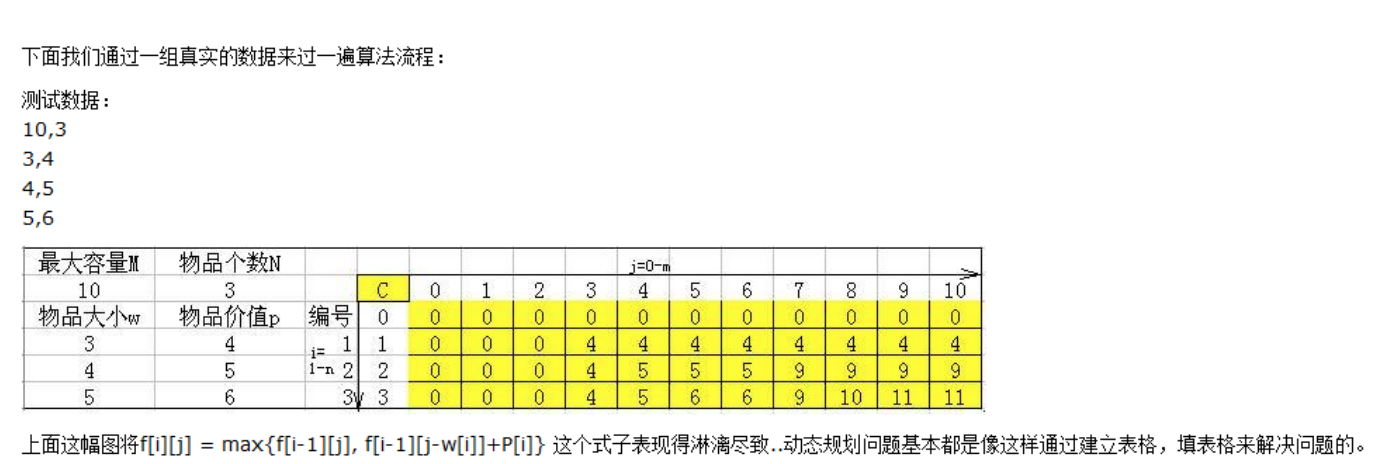
解法 2

时间复杂度 \(O(n^2)\)
空间复杂度 \(O(n)\)

#include <iostream>
#include <vector>
using namespace std;
int main () {
    int capacity = 10;
    vector<int> volumes {3, 4, 5};
    vector<int> values {4, 5, 6};  // maxValue: 11
    size_t num = volumes.size();
    if (capacity <= 0) return 0;

    // maxValue[i][j] 的含义: 将前 i 个物品中的一些物品装入容量为 j 的背包所能产生的最大价值

    // 降低空间复杂度利用递归式
    //     maxValue[i][cap] = max(maxValue[i-1][cap], maxValue[i-1][cap-volumes[i]]
    // 即 maxValue[i][j] 只依赖于 maxValue[i-1][j||k], 故第一个 axis 可以不要了, 
    // 但是 capacity 的遍历要从大到小才可以, 由于需要用到上一层前面的值, 不可以被新值覆盖

    vector<int> maxValue(capacity+1, 0);
    for (int i = 0; i < num; i++) {
        for (int cap = capacity; cap > 0; cap--) {
            if (volumes[i] <= cap) {
                maxValue[cap] = max(maxValue[cap], maxValue[cap-volumes[i]]+values[i]);
            }
        }
    }
    cout << maxValue[capacity];
    return 0;
}

解法 3

解法1,2中, maxValue[i][j]的含义: 将前 i 个物品中的一些物品装入容量为 j 的背包所能产生的最大价值
其实也可以将 maxValue[i][j]的含义解释为 将前 j 个物品中的一些物品装入容量为 i 的背包所能产生的最大价值

然而, 这种解法没法将空间复杂度降到 O(n), 由于降低空间复杂度利用的是将前 j 个物品放入容量为 i 的包中最大价值
依赖于将前 j-1 个物品放入容量为 i 的包中最大价值, 即需要二维矩阵的一行表示的前 j 物品个物体放入容量为 0~capacity 的背包中, 一行中物品的个数不变, 变化的是背包的容量.

而新解释中, 每一行背包的容量不变, 物品的个数在变化 0~N

#include <iostream>
#include <vector>
using namespace std;
int main () {
    int capacity = 10;
    if (capacity <= 0) return 0;
    vector<int> volumes {3, 4, 5};
    vector<int> values {4, 5, 6};
    size_t num = volumes.size();

    // 为了把索引从 0 开始转化为从 1 开始
    volumes.insert(volumes.begin(), 0);
    values.insert(values.begin(), 0);

    vector<vector<int>> maxValue(capacity+1, vector<int>(num+1, 0));
    for (int cap = 1; cap <= capacity; cap++) {
        for (int i = 1; i <= num; i++) {
            if (volumes[i] > cap) {
                maxValue[cap][i] = maxValue[cap][i-1];
            } else {
                maxValue[cap][i] = max(maxValue[cap][i-1], maxValue[cap-volumes[i]][i-1]+values[i]);
            }
        }
    }
    cout << maxValue[capacity][num];
    return 0;
}

实战--CPU任务分配

有一个电脑有2个cpu, 现在有n个任务, 每个任务所需时间为所需时间 \(t_i\), \(t_i\) 为正整数, 求完成全部任务的所需最小时间

这样目标转化为将 n 个任务划分为两部分a, b(a ≥ b), 使得 a-b 最小.

设 n 个任务在一个 cpu 上所需时间之和是 sum, sum = a+b

\[\begin{align*} Target &= \min(a-b) \\ &= \min((sum-b)-b) \\ &= \min(sum-2b) \\ &\approx \min(\frac{sum}{2}-b) \ge 0 \\ &\approx \max(b), \quad b \le \left\lfloor{\frac{sum}{2}} \right\rfloor \end{align*} \]

问题转化:

将 n 个任务取出来, 放在不超过 \(\left\lfloor{\frac{sum}{2}}\right\rfloor\)(背包的容量) 的背包里, b 能取得的最大值, 即背包问题. 相对应, 每个任务的时间既代表物品的容量, 也代表物品的价值

#include <iostream>
#include <vector>
#include <numeric>
using namespace std;

int main () {
    vector<int> tasks {2, 3, 4, 5, 6, 28};  // answer: 8
    int sum = accumulate(tasks.begin(), tasks.end(), 0);
    int capacity = sum / 2;
    size_t num = tasks.size();

    // maximum_value[i][j] 的含义:
    // 将前 i 个物品中的一些物品装入容量为 j 的背包所能产生的最大价值
    vector<int> maxValue(capacity+1, 0);
    for (int i = 0; i < num; i++) {
        for (int cap = capacity; cap > 0; cap--) {
            if (tasks[i] <= cap) {
                maxValue[cap] = max(maxValue[cap], maxValue[cap-tasks[i]]+tasks[i]);
            }
        }
    }
    cout << sum - 2 * maxValue[capacity] << endl;
    return 0;
}