B树和B+树的插入、删除图文详解
本文摘自:https://www.cnblogs.com/nullzx/p/8729425.html
感谢大佬nullzx的总结与分享。
另外为验证本人的正确性,通过一个小工具验证了下文中的拆入结果,感兴趣的伙伴们 可以自己动手验证。
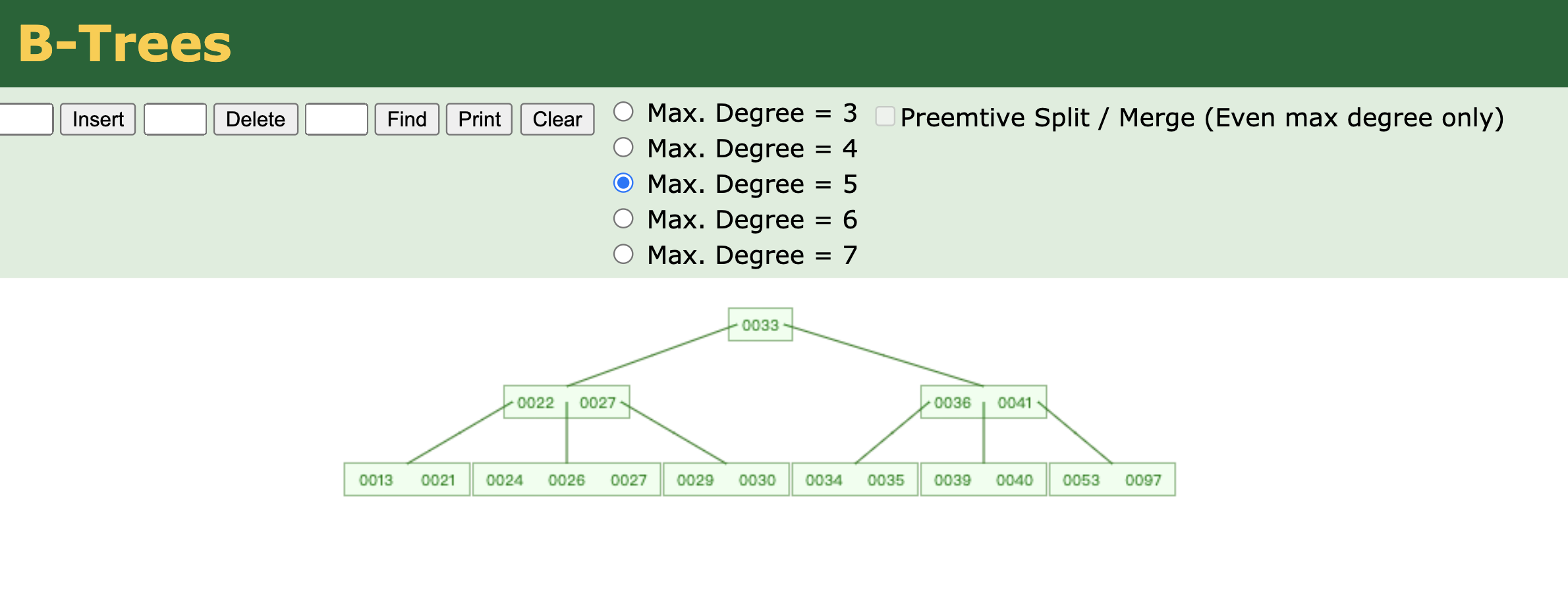
简介:本文主要介绍了B树和B+树的插入、删除操作。写这篇博客的目的是发现没有相关博客以举例的方式详细介绍B+树的相关操作,由于自身对某些细节也感到很迷惑,通过查阅相关资料,对B+树的操作有所顿悟,写下这篇博客以做记录。由于是自身对B+树的理解,肯定有考虑不周的情况,或者理解错误的地方,请留言指出。
1、B树
B树的定义
B树也称B-树,它是一颗多路平衡查找树。我们描述一颗B树时需要指定它的阶数,阶数表示了一个结点最多有多少个孩子结点,一般用字母m表示阶数。当m取2时,就是我们常见的二叉搜索树。
一颗m阶的B树定义如下:
1)每个结点最多有m-1个关键字。
2)根结点最少可以只有1个关键字。
3)非根结点至少有Math.ceil(m/2)-1个关键字。
4)每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
5)所有叶子结点都位于同一层,或者说根结点到每个叶子结点的长度都相同。

上图是一颗阶数为4的B树。在实际应用中的B树的阶数m都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小。每个结点中存储了关键字(key)和关键字对应的数据(data),以及孩子结点的指针。我们将一个key和其对应的data称为一个记录。但为了方便描述,除非特别说明,后续文中就用key来代替(key, value)键值对这个整体。在数据库中我们将B树(和B+树)作为索引结构,可以加快查询速速,此时B树中的key就表示键,而data表示了这个键对应的条目在硬盘上的逻辑地址。
B树的插入操作
插入操作是指插入一条记录,即(key, value)的键值对。如果B树中已存在需要插入的键值对,则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。
1)根据要插入的key的值,找到叶子结点并插入。
2)判断当前结点key的个数是否小于等于m-1,若满足则结束,否则进行第3步。
3)以结点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父结点中,这个key的左子树指向分裂后的左半部分,这个key的右子支指向分裂后的右半部分,然后将当前结点指向父结点,继续进行第3步。
下面以5阶B树为例,介绍B树的插入操作,在5阶B树中,结点最多有4个key,最少有2个key
a)在空树中插入39,此时根结点就一个key,此时根结点也是叶子结点
![clip_image002[4]](https://gitee.com/HNov/image/raw/master/typora/20200521152414.png)
b)继续插入22,97和41,根结点此时有4个key

c)继续插入53

插入后超过了最大允许的关键字个数4,所以以key值为41为中心进行分裂,结果如下图所示,分裂后当前结点指针指向父结点,满足B树条件,插入操作结束。当阶数m为偶数时,需要分裂时就不存在排序恰好在中间的key,那么我们选择中间位置的前一个key或中间位置的后一个key为中心进行分裂即可。

d)依次插入13,21,40,同样会造成分裂,结果如下图所示。

e)依次插入30,27, 33 ;36,35,34 ;24,29,结果如下图所示。

f)插入key值为26的记录,插入后的结果如下图所示。

当前结点需要以27为中心分裂,并向父结点进位27,然后当前结点指向父结点,结果如下图所示。

进位后导致当前结点(即根结点)也需要分裂,分裂的结果如下图所示。

分裂后当前结点指向新的根,此时无需调整。
g)最后再依次插入key为17,28,29,31,32的记录,结果如下图所示。

在实现B树的代码中,为了使代码编写更加容易,我们可以将结点中存储记录的数组长度定义为m而非m-1,这样方便底层的结点由于分裂向上层插入一个记录时,上层有多余的位置存储这个记录。同时,每个结点还可以存储它的父结点的引用,这样就不必编写递归程序。
一般来说,对于确定的m和确定类型的记录,结点大小是固定的,无论它实际存储了多少个记录。但是分配固定结点大小的方法会存在浪费的情况,比如key为28,29所在的结点,还有2个key的位置没有使用,但是已经不可能继续在插入任何值了,因为这个结点的前序key是27,后继key是30,所有整数值都用完了。所以如果记录先按key的大小排好序,再插入到B树中,结点的使用率就会很低,最差情况下使用率仅为50%。
B树的删除操作
删除操作是指,根据key删除记录,如果B树中的记录中不存对应key的记录,则删除失败。
1)如果当前需要删除的key位于非叶子结点上,则用后继key(这里的后继key均指后继记录的意思)覆盖要删除的key,然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上,这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步
2)该结点key个数大于等于Math.ceil(m/2)-1,结束删除操作,否则执行第3步。
3)如果兄弟结点key个数大于Math.ceil(m/2)-1,则父结点中的key下移到该结点,兄弟结点中的一个key上移,删除操作结束。
否则,将父结点中的key下移与当前结点及它的兄弟结点中的key合并,形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,重复上第2步。
有些结点它可能即有左兄弟,又有右兄弟,那么我们任意选择一个兄弟结点进行操作即可。
下面以5阶B树为例,介绍B树的删除操作,5阶B树中,结点最多有4个key,最少有2个key
a)原始状态

b)在上面的B树中删除21,删除后结点中的关键字个数仍然大于等2,所以删除结束。

c)在上述情况下接着删除27。从上图可知27位于非叶子结点中,所以用27的后继替换它。从图中可以看出,27的后继为28,我们用28替换27,然后在28(原27)的右孩子结点中删除28。删除后的结果如下图所示。

删除后发现,当前叶子结点的记录的个数小于2,而它的兄弟结点中有3个记录(当前结点还有一个右兄弟,选择右兄弟就会出现合并结点的情况,不论选哪一个都行,只是最后B树的形态会不一样而已),我们可以从兄弟结点中借取一个key。所以父结点中的28下移,兄弟结点中的26上移,删除结束。结果如下图所示。

d)在上述情况下接着32,结果如下图。

当删除后,当前结点中只key,而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并,成为一个新的结点,当前结点的指针指向父结点。结果如下图所示。

当前结点key的个数满足条件,故删除结束。
e)上述情况下,我们接着删除key为40的记录,删除后结果如下图所示。

同理,当前结点的记录数小于2,兄弟结点中没有多余key,所以父结点中的key下移,和兄弟(这里我们选择左兄弟,选择右兄弟也可以)结点合并,合并后的指向当前结点的指针就指向了父结点。

同理,对于当前结点而言只能继续合并了,最后结果如下所示。

合并后结点当前结点满足条件,删除结束。
2. B+树
B+树的定义

各种资料上B+树的定义各有不同,一种定义方式是关键字个数和孩子结点个数相同。这里我们采取维基百科上所定义的方式,即关键字个数比孩子结点个数小1,这种方式是和B树基本等价的。上图就是一颗阶数为4的B+树。
除此之外B+树还有以下的要求。
1)B+树包含2种类型的结点:内部结点(也称索引结点)和叶子结点。根结点本身即可以是内部结点,也可以是叶子结点。根结点的关键字个数最少可以只有1个。
2)B+树与B树最大的不同是内部结点不保存数据,只用于索引,所有数据(或者说记录)都保存在叶子结点中。
3) m阶B+树表示了内部结点最多有m-1个关键字(或者说内部结点最多有m个子树),阶数m同时限制了叶子结点最多存储m-1个记录。
4)内部结点中的key都按照从小到大的顺序排列,对于内部结点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
5)每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
B+树的插入操作
1)若为空树,创建一个叶子结点,然后将记录插入其中,此时这个叶子结点也是根结点,插入操作结束。
2)针对叶子类型结点:根据key值找到叶子结点,向这个叶子结点插入记录。插入后,若当前结点key的个数小于等于m-1,则插入结束。否则将这个叶子结点分裂成左右两个叶子结点,左叶子结点包含前m/2个记录,右结点包含剩下的记录,将第m/2+1个记录的key进位到父结点中(父结点一定是索引类型结点),进位到父结点的key左孩子指针向左结点,右孩子指针向右结点。将当前结点的指针指向父结点,然后执行第3步。
3)针对索引类型结点:若当前结点key的个数小于等于m-1,则插入结束。否则,将这个索引类型结点分裂成两个索引结点,左索引结点包含前(m-1)/2个key,右结点包含m-(m-1)/2个key,将第m/2个key进位到父结点中,进位到父结点的key左孩子指向左结点, 进位到父结点的key右孩子指向右结点。将当前结点的指针指向父结点,然后重复第3步。
下面是一颗5阶B树的插入过程,5阶B数的结点最少2个key,最多4个key。
a)空树中插入5

b)依次插入8,10,15

c)插入16

插入16后超过了关键字的个数限制,所以要进行分裂。在叶子结点分裂时,分裂出来的左结点2个记录,右边3个记录,中间key成为索引结点中的key,分裂后当前结点指向了父结点(根结点)。结果如下图所示。

当然我们还有另一种分裂方式,给左结点3个记录,右结点2个记录,此时索引结点中的key就变为15。
d)插入17

e)插入18,插入后如下图所示

当前结点的关键字个数大于5,进行分裂。分裂成两个结点,左结点2个记录,右结点3个记录,关键字16进位到父结点(索引类型)中,将当前结点的指针指向父结点。

当前结点的关键字个数满足条件,插入结束。
f)插入若干数据后

g)在上图中插入7,结果如下图所示

当前结点的关键字个数超过4,需要分裂。左结点2个记录,右结点3个记录。分裂后关键字7进入到父结点中,将当前结点的指针指向父结点,结果如下图所示。

当前结点的关键字个数超过4,需要继续分裂。左结点2个关键字,右结点2个关键字,关键字16进入到父结点中,将当前结点指向父结点,结果如下图所示。

当前结点的关键字个数满足条件,插入结束。
B+树的删除操作
如果叶子结点中没有相应的key,则删除失败。否则执行下面的步骤
1)删除叶子结点中对应的key。删除后若结点的key的个数大于等于Math.ceil(m-1)/2 – 1,删除操作结束,否则执行第2步。
2)若兄弟结点key有富余(大于Math.ceil(m-1)/2 – 1),向兄弟结点借一个记录,同时用借到的key替换父结(指当前结点和兄弟结点共同的父结点)点中的key,删除结束。否则执行第3步。
3)若兄弟结点中没有富余的key,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的key(父结点中的这个key两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第4步(第4步以后的操作和B树就完全一样了,主要是为了更新索引结点)。
4)若索引结点的key的个数大于等于Math.ceil(m-1)/2 – 1,则删除操作结束。否则执行第5步
5)若兄弟结点有富余,父结点key下移,兄弟结点key上移,删除结束。否则执行第6步
6)当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点,重复第4步。
注意,通过B+树的删除操作后,索引结点中存在的key,不一定在叶子结点中存在对应的记录。
下面是一颗5阶B树的删除过程,5阶B数的结点最少2个key,最多4个key。
a)初始状态

b)删除22,删除后结果如下图

删除后叶子结点中key的个数大于等于2,删除结束
c)删除15,删除后的结果如下图所示

删除后当前结点只有一个key,不满足条件,而兄弟结点有三个key,可以从兄弟结点借一个关键字为9的记录,同时更新将父结点中的关键字由10也变为9,删除结束。

d)删除7,删除后的结果如下图所示

当前结点关键字个数小于2,(左)兄弟结点中的也没有富余的关键字(当前结点还有个右兄弟,不过选择任意一个进行分析就可以了,这里我们选择了左边的),所以当前结点和兄弟结点合并,并删除父结点中的key,当前结点指向父结点。

此时当前结点的关键字个数小于2,兄弟结点的关键字也没有富余,所以父结点中的关键字下移,和两个孩子结点合并,结果如下图所示。

参考内容
[1] B+树介绍
[2] 从MySQL Bug#67718浅谈B+树索引的分裂优化
[3] B+树的几点总结



