2022牛客暑期多校集训解题报告 第一场
A. Villages: Landlines(区间合并)
题意 :给定n - 1个建筑和一个发电站,分布在一个一维的数轴上,这n - 1个建筑都有各自的电力接受范围,不连通的建筑可以通过电相连,问使每个建筑都通上电所需的最小电线长度
思路 :将每个建筑看成区间,然后问题就转化为区间贪心问题,将断开的区间补上即可
ac代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <queue>
#include <map>
#include <vector>
#include <stack>
#include <set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#include <unordered_set>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0);
#define endl '\n'
#define pb push_back
#define all(x) x.begin(),x.end()
#define all1(x) x.begin()+1,x.end()
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 300010,M = 200010,INF = 0x3f3f3f3f,mod = 1e9 + 7;
const double INFF = 0x7f7f7f7f7f7f7f7f,pi = acos(-1.0);
int n,m,k,t;
int main()
{
ios;
cin >> n;
vector<PII> a(n + 1);
for(int i = 1;i <= n ;i ++)
{
int l,r;
cin >> l >> r;
a[i] = {l - r,l + r};
}
sort(all1(a));
int r = a[1].y;
int ans = 0;
for(int i = 2;i <= n;i ++)
{
if(a[i].x > r) ans += a[i].x - r;
r = max(r,a[i].y);
}
cout << ans << endl;
return 0;
}
C. Grab the Seat!(枚举 + 思维)
题意 :教室中有n * m 个座位,定义一个座位未被阻挡位为任意一个位置不会阻挡其看黑板的视线,教室中有k个人,每次改变一个人的位置,问有多少个座位为被阻挡
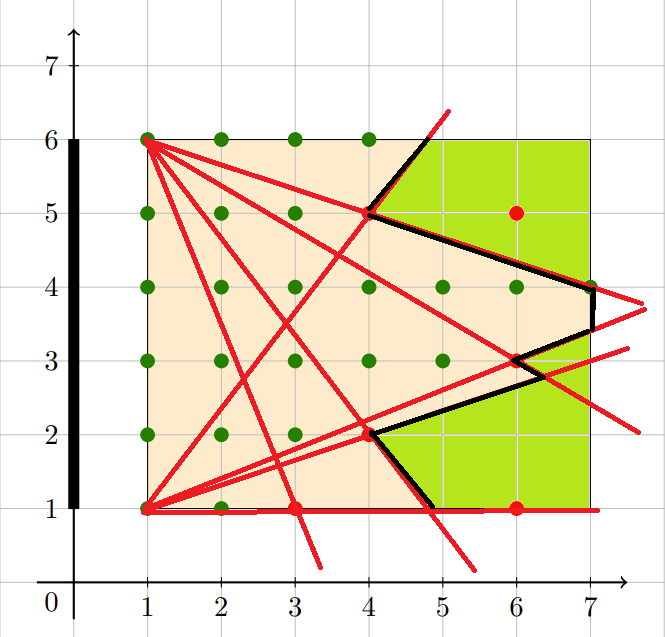
分析 : 如图对于一个人所阻挡得范围为黑板两端与其连线后面的三角形区域,那么我们只需要求出每个人的范围然后取并,再求个补集即可,可以发现每一行的最靠前有人的位置会遮挡住该行其他人,所以我们按行枚举这个位置即可,注意正反两次枚举
ac 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <queue>
#include <map>
#include <vector>
#include <stack>
#include <set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#include <unordered_set>
#include <random>
//#pragma GCC optimize(3)
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0);
#define endl '\n'
#define pb push_back
#define all(x) x.begin(),x.end()
#define all1(x) x.begin()+1,x.end()
using namespace std;
typedef unsigned long long uLL;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 10010,INF = 0x3f3f3f3f,mod = 1e9 + 7;
const double INFF = 0x7f7f7f7f7f7f7f7f,pi = acos(-1.0);
int n,m,k,t;
int a[N],b[N];
void solve()
{
vector<int> p(m),ans(m + 1);
for(int i = 0;i < m;i ++) p[i] = n + 1;
for(int i = 1;i <= k;i ++) p[b[i] - 1] = min(p[b[i] - 1], a[i]);
for(int i = 0;i < m;i ++) ans[i] = p[i] - 1;
int x = n + 1,y = 0;
for(int i = 0;i < m;i ++)
{
int x1 = p[i],y1 = i;
if(1LL* y1 * x >= 1LL * y * x1) x = x1,y = y1;
int t = n;
if(y) t = (1LL* y1 * x - 1) / y;
ans[i] = min(t,ans[i]);
}
reverse(all(p));
x = n + 1,y = 0;
for(int i = 0;i < m;i ++)
{
int x1 = p[i],y1 = i;
if(1LL* y1 * x >= 1LL * y * x1) x = x1,y = y1;
int t = n;
if(y) t = (1LL* y1 * x - 1) / y;
ans[m - 1 - i] = min(t,ans[m - 1 - i]);
}
LL res = 0;
for(int i = 0;i < m;i ++) res += ans[i];
cout << res << endl;
}
int main()
{
ios;
cin >> n >> m >> k >> t;
for(int i = 1;i <= k;i ++) cin >> a[i] >> b[i];
while(t --)
{
int x;
cin >> x >> a[x] >> b[x];
solve();
}
return 0;
}
D. Mocha and Railgun(数学)
题意 :有一个圆 给定一个定长的线段,令这个线段绕其中点旋转,问该线段在圆周上的最长投影长度
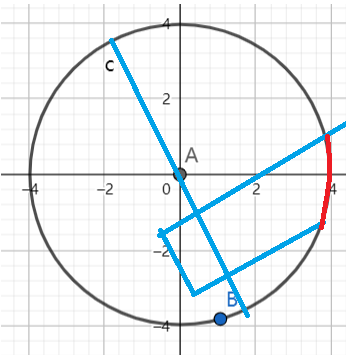
思路:如图可以发现不管这条线段如何旋转,他都可以投影至某条直径上在进行圆周上投影,因此该问题可转化为一条定长线段在直径上平移,当线段平移至离圆心最远时投影长度最长
ac 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <queue>
#include <map>
#include <vector>
#include <stack>
#include <set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#include <unordered_set>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0);
#define endl '\n'
#define pb push_back
#define all(x) x.begin(),x.end()
#define all1(x) x.begin()+1,x.end()
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 200010,INF = 0x3f3f3f3f,mod = 998244353;
const double INFF = 0x7f7f7f7f7f7f7f7f;
int n,m,k,t;
LL f[20][100];
int main()
{
ios;
cin >> t;
while(t --)
{
LL a,b,r,d;
cin >> r >> a >> b >> d;
double x = sqrt( a * a + b * b),y = 0;
double x1 = x + d,x2 = x - d,dx = 2 * d;
double y1 = sqrt(r * r - x1 * x1),y2 = sqrt(r * r - x2 * x2),dy = fabs(y2 - y1);
double len = sqrt(dx * dx + dy * dy) / 2;
double sina = len / r;
double A = asin(sina) * 2;
cout << fixed << setprecision(12) << A * r << endl;
}
return 0;
}
G. Lexicographical Maximum(贪心)
题意 :给定一个数字 n 问1~n中字典序最大的数字是多少
分析:贪心
ac 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <queue>
#include <map>
#include <vector>
#include <stack>
#include <set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#include <unordered_set>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0);
#define endl '\n'
#define pb push_back
#define all(x) x.begin(),x.end()
#define all1(x) x.begin()+1,x.end()
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 200010,INF = 0x3f3f3f3f,mod = 998244353;
const double INFF = 0x7f7f7f7f7f7f7f7f;
int n,m,k,t;
LL f[20][100];
int main()
{
ios;
string s;
cin >> s;
bool success = true;
for(int i = 0;i < s.size() - 1;i ++) if(s[i] != '9') success = false;
if(success) cout << s <<endl;
else
{
n = s.size() - 1;
while(n --) cout << 9;
}
return 0;
}
I. Chiitoitsu(dp预处理)
题意:日本麻将,凑对子,问凑成七对对子的期望轮数
分析:定义 \(f(i,j)\) 为目前手中有i对对子,还可摸j张牌的期望轮数,最优策略为每次摸一张牌,如果能凑成一个对子就打出去一个单,不能就打回去
对于可以凑成的情况,\(f(i,j) = f(i + 1,j - 1) * has / j\)
对于不难凑成的情况,\(f(i,j) = f(i,j - 1) * hasn / j\)
ac代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <queue>
#include <map>
#include <vector>
#include <stack>
#include <set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#include <unordered_set>
#include <random>
//#pragma GCC optimize(3)
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0);
#define endl '\n'
#define pb push_back
#define all(x) x.begin(),x.end()
#define all1(x) x.begin()+1,x.end()
using namespace std;
typedef unsigned long long uLL;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 10010,INF = 0x3f3f3f3f,mod = 1e9 + 7;
const double INFF = 0x7f7f7f7f7f7f7f7f,pi = acos(-1.0);
int n,m,k,t;
int a[N],b[N];
int qmi(int a,int k)
{
int res = 1;
while(k)
{
if(k & 1) res = 1LL * res * a % mod;
k >>= 1;
a = 1LL * a * a % mod;
}
return res;
}
LL f[20][150];
void dp()
{
for(int i = 6;~ i;i --)
{
int has = (13 - i * 2) * 3;
for(int j = has;j <= 123;j ++)
{
int inv = qmi(j,mod - 2);
int hasn = j - has;
f[i][j] = (f[i + 1][j - 1] % mod * has % mod * inv % mod + f[i][j - 1] % mod * hasn % mod * inv % mod + 1) % mod;
}
}
}
int main()
{
ios;
dp();
cin >> t;
while(t --)
{
map<string,int> mp;
string s;
int Pair = 0;
cin >> s;
for(int i = 0;i < s.size();i += 2)
{
if(mp[s.substr(i,2)]) Pair ++;
mp[s.substr(i,2)] = 1;
}
cout << "Case #" << ++ k << ": " << f[Pair][123] << endl;
}
return 0;
}

