Codeforces Round #802 (Div. 2) 解题报告
A. Optimal Path
题意 : 给定一个二维矩阵,如下图一样编号,问从左上角到右下角的的所有路径中经过格子上的数的和的最小值
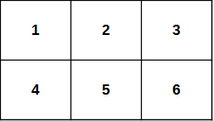
分析:贪心,先一直走到右上角,再走到右下角
ac代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pb push_back
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;
int n,m,k,t;
int main()
{
ios;
cin >> t;
while(t --)
{
cin >> n >> m;
//if(m < n) swap(n,m);
LL ans = 0;
for(int i = 1;i < m;i ++) ans += i;
for(int i = 1;i <= n;i ++) ans += m * i;
cout << ans << endl;
}
return 0;
}
B. Palindromic Numbers
题意:给定一个长度为n的数字a,求一个长度也为n的数字b,使得a + b 为一个回文数字
分析:直接让每一位都变成9,如果第一位有前导零,那就使b = x - a,x为长度为n + 1且每一位都是1的数字
c++要用到高精度
ac代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pb push_back
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;
int n,m,k,t;
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
reverse(C.begin(),C.end());
return C;
}
int main()
{
ios;
cin >> t;
while(t --)
{
string s,x;
cin >> n >> s;
string ans = "";
vector<int> a,b;
bool f = true;
for(int i = 0;i < n;i ++)
{
if(s[i] != '9') f = false;
ans += char(9 - (s[i] - '0') + 48);
}
if(ans[0] != '0') cout << ans << endl;
else
{
string x(n + 1 ,'1');
for(int i = n - 1;i >= 0;i --) a.pb(s[i] - '0');
for(int i = n ;i >= 0;i --) b.pb(x[i] - '0');
auto c = sub(b,a);
for(int i = 0;i < c.size();i ++) cout << c[i];
cout << endl;
}
}
return 0;
}
C. Helping the Nature
题意:给定一个长度为n的数组,定义如下操作
1.选择i() ,使的每一个数字都减一
2.选择i() ,使的每一个数字都减一
3.使全部数字都加1
问使得全部数字变为0的最小操作数
分析:
使得全部数都变为0等价于使差分数组全变为0,
用差分的操作来转换以上操作
1.b[1] -= 1,b[i + 1] += 1
2.b[i] -= 1
3.b[1] += 1
这样就使得区间操作变为单点操作,再逐步考虑贪心,我们发现操作一在操作其他数字的时候会影响到b[1]的值,而操作3可以抵消其影响,所以,我们先考虑2到n上的数字,贪心地将每一位数字都变为0,最后再考虑将b[1]变为0
ac代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pb push_back
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;
int n,m,k,t;
int main()
{
ios;
cin >> t;
while(t --)
{
cin >> n;
vector<int> a(n + 1);
vector<LL> b(n + 2,0);
for(int i = 1;i <= n;i ++) cin >> a[i],b[i] += a[i],b[i + 1] -= a[i];
LL ans = 0;
for(int i = 2;i <= n;i ++)
{
if(b[i] < 0) b[1] += b[i],ans -= b[i];
else if(b[i] > 0) ans += b[i];
}
cout << ans+ LL(abs(b[1])) << endl;
}
return 0;
}
D. River Locks
题意 : 有连续地一系列水池,每个水池上面都有一个进水管,进水速率均为1升/秒,每个水池的容积为,进水时,水池满后会流向下游水池,进行q次询问,每次询问在时间内使得全部水池变满所开水管的数量的最小值

分析:由于水会流向下游,所以我们尽量开上游的水池
假设1到i的水闸开启,sum为1到i水池的容积和,则使得这些水池都装满的最小时间为,由此可得最小开闸数量为,对于每个水池其水满最小时间与上述前缀水池都装满等价,则这些水池装满的最小时间的最大值即为可行的最小边界,
ac代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream>
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pb push_back
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;
int n,m,k,t;
int main()
{
ios;
cin >> n;
LL sum = 0;
int x,maxv = 0;
for(int i = 1;i <= n;i ++) cin >> x,sum += x,maxv = max(LL(maxv),(sum + i - 1) / i);
cin >> n;
while(n --)
{
cin >> x;
if(x < maxv) cout << -1 << endl;
else cout << (sum + x - 1) / x << endl;
}
return 0;
}
本文作者:notyour_young
本文链接:https://www.cnblogs.com/notyour-young/p/16394985.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步