Codeforces Round #788 (Div. 2)解题报告

A. Prof. Slim

题意：给定一个长度为n的整数数列，可以选定一个正数和一个负数交换他们的符号，问是否能将其构造成非递减序列
把所有的负号放前面，检查一下是否非递减即可
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream> 
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 998244353 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,x;
int a[N];


int main()
{
	ios;
	int t;
	cin >> t;
	while(t --)
	{
		bool f = true;
		int sum = 0;
		cin >> n;
		for(int i = 1;i <= n;i ++) 
		{
			cin >> a[i];
			if(a[i] < 0) sum ++;
		}
		for(int i = 1; i <= n;i ++)
		{
			if(i <= sum) a[i] = - abs(a[i]);
			else a[i] = abs(a[i]);
		}

		for(int i = 2;i <= n;i ++)
		{
			if(a[i] < a[i - 1]) 
			{
				f = false;
				break;
			}
		}
		if(f) cout << "YES" << endl;
		else cout << "NO" << endl;
	}
	return 0;
}

B. Dorms War

题意：给定一个长度为n的字符串，和k个特殊字符，定义操作：将字符串内所有特殊字符前的一个字符删除，问最多可做多少次这样的操作。
特殊字符将整个字符串分为几段区间，取区间长度最大的即可
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream> 
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 998244353 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,x;
int a[N];


int main()
{
	ios;
	int t;
	cin >> t;
	while(t --)
	{
		string s;
		cin >> n >> s;
		map<char,int> mp;
		cin >> x;
		for(int i = 0;i < x;i ++) 
		{
			char c;
			cin >> c;
			mp[c] ++;
		}

		int maxv = 0,t = 0;
		for(int i = 0;i < n;i ++)
		{
			if(mp[s[i]] == 0) t ++;
			else 
			{
				maxv = max(maxv,t);
				t = 1;
			}
		}

		cout << maxv << endl;

	}
	return 0;
}

C. Where is the Pizza?

题意：给定两个长度为n的排列a,b,c[i] 为 a[i] or b[i],有些c[i] 已经给定,求使得c也为一个排列的方案数。
对位置分组，使得每组中的数字个数都是二，对一个组内讨论，任取一个位置，如果这个选择确定了的话，那么相应的组内有这个数字的另外一个位置选择也被确定，....，最终会发现每组只有两种方案，如果对于一个组内有一个位置已经被选，那么就只有一种方案，最后分类计数原理，每组方案数相乘即可。
也可以 看作是建图找环，每个环就是上面说的组，用并查集维护即可。
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream> 
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,x;
int a[N],b[N],c[N];
int p[N];
bool st[N];
int find(int x)
{
	if(x != p[x]) return p[x] = find(p[x]);
	return x;
}

LL qmi(int a,int k,int p)
{
	LL res = 1;
	while(k)
	{
		if(k & 1) res = 1LL * res * a % p;
		k >>= 1;
		a = 1LL * a * a % p;
	}
	return res;
}

int main()
{
	ios;
	int t;
	cin >> t;
	while(t --)
	{
		cin >> n;
		vector<PII> v;
		for(int i = 1; i <= n;i ++) p[i] = i;
		memset(st,0,sizeof (bool) * (n + 4));
		for(int i = 0;i < n;i ++) cin >> a[i];

		for(int i = 0;i < n;i ++) cin >> b[i];

		for(int i = 0;i < n;i ++) cin >> c[i];

		int cnt = 0;
		for(int i = 0;i < n;i ++)
		{
			int x = find(a[i]),y = find(b[i]);
			if(x != y)
			{
				p[x] = y;
			}
			else cnt ++;

		}

		for(int i = 0;i < n;i ++)
		{
			if(c[i])
			{
				int x = find(c[i]);
				if(!st[x])
				{
					cnt --;
					st[x] = true;
				}
			}
			else if(a[i] == b[i])
			{
				int x = find(a[i]);
				if(!st[x])
				{
					cnt --;
					st[x] = true;
				}
			}
		}

		cout << qmi(2,cnt,mod) << endl;		
	}
	return 0;
}

D. Very Suspicious

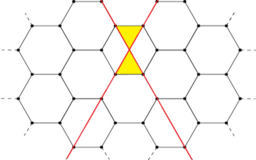
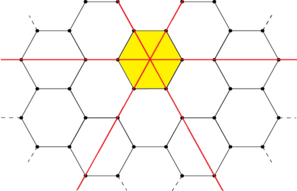
题意：给定一个蜂窝图，问最少切几刀可以获得n个等边三角形。刀只能有三种角度（相较x轴）：\(0^。,60^。,120^。\)
画图模拟，可以发现每切一刀增加的三角形数量为与其相交的直线的数量 * 2，贪心的切，找到规律
为 0 2 4 | 4 6 8 | 8 10 12，打表做前缀和再二分即可,a[i] = (a[i - 3] / 2 - 2) * 2.


ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include <sstream>
#include <fstream> 
#include <cmath>
#include <iomanip>
#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 1000010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,x;
LL a[N],b[N],c[N];
bool st[N];

int main()
{
	ios;
	int idx = 1;
	a[2] = 2,a[3] = 4;
	for(int i = 4;i <= 40000;i ++)
	{
		a[i] = (a[i - 3] / 2 + 2) * 2;
	}
	for(int i = 1;i <= 40000;i ++) a[i] += a[i - 1];
	int t;
	cin >> t;
	while(t --)
	{
		cin >> n;
		int l = 1,r = 40000 - 1;
		while(l < r)
		{
			int mid = l + r >> 1;
			if(a[mid] >= n) r = mid;
			else l = mid + 1;
		}
		cout << l << endl;
	}
	return 0;
}