Codeforces Round #786 (Div. 3) 解题报告

A. Number Transformation

题意：t组数据，每组两个数字x, y 问是否存在一对正整数a, b使得\(x * b ^ a = y\) ,若有则输出任意一对a, b，否则输出 0 0。
水题判断 y 能不能被x整除即可，因为答案不唯一，所以输出 1 和 y / x 即可
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include<deque>
#include <sstream>
//#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 100010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,a[N];

int main()
{
	//ios;
	int t;
	cin >> t;
	while(t --)
	{
		int x,y;
		cin >> x >> y;
		if(x > y || y % x) cout << "0 0" << endl;
		else
		{
			cout << 1 << " " << y / x << endl;
		}

	}
	return 0;
}

B. Dictionary

题意：给定一个由两个不同字母组成的字符串，规定所有的这样的字符按字典序排列，从1开始顺序编号，问给的字符串代表多少。
构造即可
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include<deque>
#include <sstream>
//#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 100010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,a[N];

int main()
{
	//ios;
	map<string,int> mp;
	char x = 'a',y = 'b';
	for(int i = 1;i <= 650;i ++)
	{
		string s;
		s += x;
		s += y;
		mp[s] = i;
		y ++;
		if(y > 'z') y = 'a',x ++;
		else if(x == y) y ++;
	}
	int t;
	cin >> t;
	while(t --)
	{
		string s;
		cin >> s;
		cout << mp[s] << endl;
	}
	return 0;
}

C. Infinite Replacement

题意：给定两个字符串s 和 t，s里全是'a',我们可以将s里的任意几个'a'变为字符串t，假若t里有'a',也可以将这个'a'变为t，问我们可以得到多少不同的字符串，如果无限大就输出-1.
很明显如果t里有a就可以无限套娃，结果肯定无限大，就输出-1，但要特判 t == "a"的情况，这样只能是1，若t中没有'a'，那么我们可以从将s中的几个位置变成t这个角度考虑，推出式子\(ans = C^0_n + C^1_n + C ^ 2 _ n + ...... + C^n_n = 2 ^ n\),所以输出(LL)1 << s.s.size()即可
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include<deque>
#include <sstream>
//#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 100010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,a[N];

int main()
{
	//ios;
	int t;
	cin >> t;
	while(t --)
	{
		string s,t;
		cin >> s >> t;
		int a = s.size();
		int num = 0;
		for(int i = 0;i < t.size();i ++) if(t[i] == 'a') num ++;
		if(num && t.size() == 1)
		{
			cout << 1 << endl;
		}
		else if(num && t.size() != 1) cout << -1 << endl;
		else cout << ((LL)1 << a) << endl; 
	}
	return 0;
}

D. A-B-C Sort

题意：有 a,b,c三个数组，初始时a有n个数，b, c为空，进行如下操作。

第1步：当a不是空的时候，你从a中取出最后一个元素并将其移到数组b的中间，b中有奇数个数时，可以选择放在中间那个数的左边或右边。
第二步：当b不为空时，你从b中取出中间元素并将其移到数组c的末端，当b中有偶数个数时，可以选择拿中间那两个数的任意一个。结果，b变成空的，c现在由n个元素组成。

问能否将c构造为非递减序列。
分析：
手动模拟几个数据，会发现最后c中的每段以2为长度的两个数一定是原来a数组中的那两个数，具体原因很难描述，和插入过程中被插入序列的长度有关，当为偶数时只能插入中间，为奇数时选择左右，两种情况交替出现，所以这个唬人的操作其实就是for(int i = pos;i <= n - 1;i += 2) if(a[i] > a[i + 1]),swap(a[i],a[i + 1]);同时注意特判数组长度的奇偶性，为奇数时pos = 2,否则为 1.
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include<deque>
#include <sstream>
//#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,a[N];

int main()
{
	ios;
	int t;
	cin >> t;
	while(t --)
	{
		cin >> n;
		for(int i = 1;i <= n;i ++) cin >> a[i];
		int pos;
		if(n % 2 ) pos = 2;
		else pos = 1;
		for(;pos <= n - 1;pos += 2)
		{
			if(a[pos] > a[pos + 1]) swap(a[pos],a[pos + 1]);
		}
		bool f = true;
		for(int i = 1;i <= n - 1;i ++)
			if(a[i] > a[i + 1]) 
			{
				f = false;
				break;
			}
		if(f) cout << "YES" << endl;
		else cout << "NO" << endl;
	}
	return 0;
}

E. Breaking the Wall

题意：给定一个由n个数字组成的数组a，我们可以做如下操作：

选择一个a[i],使得a[i] - 2, a[i - 1] - 1,a[i + 1] - 1
贪心
最终解的情况无外乎3种
1.两个位置连续
2.两个位置相隔1
3.两位置离散

分别对3种情况进行贪心：
1.连续
有两种情况：记maxv,minv分别为最大值，最小值：
1.当 maxv >= minv * 2 时，说明仅对大的那个进行操作就可以顺带把小的也消灭掉，则ans = (maxv + 1) / 2;
2.当 maxv < minv * 2 时,说明仅操作一个无法消灭全部，此时可以把他俩看成一个整体，每次操作会使整体 - 3，此时 ans = (maxv + minv) / 3 + (int)((maxv+ minv) % 3 != 0);

2.相隔1
贪心策略：先把二者的公共部分消灭掉，此时就剩一个，集火消除剩下的即可，ans = minv + (maxv - minv + 1) / 2;

3.离散
分别对最小和次小的进行操作，ans = (a + 1) / 2 + (b + 1) / 2;

ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include<deque>
#include <sstream>
//#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 200010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,a[N],b[N];
int ans = INF;

int main()
{
	ios;
	cin >> n;
	for(int i = 1;i <= n;i ++) cin >> a[i];

	for(int i = 1;i <= n - 1;i ++)
	{
		if(max(a[i],a[i + 1]) >= 2 * min(a[i],a[i + 1]))
		{
			ans = min(ans,(max(a[i] , a[i + 1]) + 1) / 2);
		}
		else
		{
			ans = min(ans,(a[i] + a[i + 1]) / 3 + (int)((a[i] + a[i + 1]) % 3 != 0) );
		}
	}

	for(int i = 2;i <= n - 1;i ++)
	{
		int t = (abs(a[i + 1] - a[i - 1]) + 1) / 2;
		ans = min(ans,min(a[i + 1],a[i - 1]) + t);

	}

	sort(a + 1,a + 1 + n);

	ans = min(ans,(a[1] + 1) / 2 + (a[2] + 1) / 2);

	cout << ans << endl;

	return 0;
}

F. Desktop Rearrangement

题意：给定仅由'.','*' 组成的二维矩阵，为了理解我以下面图示的方式编号（就是window系统桌面的排列顺序），每次操作对应着删除/添加'*'，问操作后为了让所有的'*'都紧凑排到前面去，应该最少移动的'*'的数量。

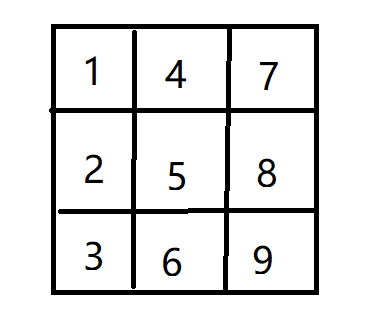
二维转为一维，很明显是个动态维护前缀和的问题，用树状数组即可,每次询问计算出在目标区域以外的'*'个数。
ac代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
#include<set>
#include<deque>
#include <sstream>
//#include <unordered_map>
#define x first
#define y second
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define pi 3.14159265358979323846
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
 
const int N = 1000010,M = 500010,INF = 0x3f3f3f3f,mod = 1e9 + 7 ;
const double INFF = 0x7f7f7f7f7f7f7f7f;

int n,m,q;
char g[1010][1010];
int tr[N];

int lowbit(int x)
{
	return x & - x;
}

void add(int x,int v)
{
	for(int i = x;i <= n * m;i += lowbit(i)) tr[i] += v;
}

LL query(int x)
{
	LL res = 0;
	for(int i = x;i;i -= lowbit(i)) res += tr[i];
	return res;
}

int get(int x,int y)
{
	return (y - 1) * n + x;
}

int main()
{
	ios;
	cin >> n >> m >> q;
	for(int i = 1;i <= n;i ++) 
		for(int j = 1;j <= m;j ++) 
			cin >> g[i][j];
	for(int j = 1;j <= m;j ++)
		for(int i = 1;i <= n;i ++) if(g[i][j] == '*') add(get(i,j), 1);

	while(q --)
	{
		int x,y;
		cin >> x >> y;
		int pos = get(x,y);
		if(g[x][y] == '.') 
		{
			g[x][y] = '*';
			add(pos, 1);

		}
		else
		{
			g[x][y] = '.';
			add(pos, -1);
		}
		int res = query(get(n,m));
		cout << res - query(res) << endl;
	}

	return 0;
}

经验总结：

别用google翻译，别用google翻译，别用google翻译
读题要读全，多看看样例的解释
没有思路时，多在草稿纸上模拟一下

posted @ 2022-05-03 19:48 notyour_young 阅读(43) 评论(2) 编辑收藏举报

刷新页面返回顶部

notyour-young