【Luogu P4809】[CCC 2018]最大战略储备

Luogu P4809

这题很显然是要求最小生成树，但是看到数据范围，边数和点数都非常的多，所以暴力Kruskal并不可行。

优化求最小生成树的算法流程明显不可行，因为如果可优化的话那么这个算法的优化应该早就广为人知了。

所以从另一个方向想，找找这题的特殊性质。

我们可以发现每个星球内部的\(P\)条航线的结构是一样的，而对于星球之间的城市的\(Q\)个港口结构也是一样的。Kruskal的算法流程中我们会对边按权值排序，换而言之：对于每个星球内部的同一类航线，由于权值相等，只要端点还不联通，我们都会选出来；对于港口同理。

那么也就是说我们只需要考虑\(P+Q\)条边即可，每次决策都相当于决策了一大堆边。

但是尽管我们一次可以选出很多条边，但是我们不难发现一个问题，每次连的边的数量并不一定是\(n\)或者\(m\)条。

利用样例举个例子：

2 2 1 2
1 2 1
2 1 1
2 1 1

可以发现我们会选择1 2 1和2 1 1这条边。对于第一条边，我们需要加入两条；对于第二条，如果加入两条，明显有一条可以去除。

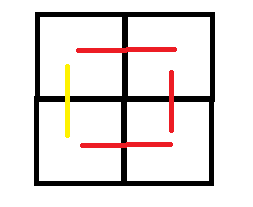
很明显，黄色的边是不必要的。

那么如何具体的求出这个数量成为了当前要解决的问题。

考虑连一条边造成了什么影响。

从网格图上看，可以认为第一条边连上去之后把第一列和第二列合并了。换而言之，少了一列，那么连列内部的边时就少了一条。

所以，每连一条航线，就会让下一次选出港口时需要的数量\(-1\)，反之亦然。

#include<cstdio>
#include<algorithm>
#define int long long
using namespace std;
int n,m,p,q,size[100005][2],fa[100005][2],u,v,w,cnt,ans;
struct DATA
{
	int to,sta,val,flag;
	bool operator<(const DATA &x) const 
	{
		return val<x.val;
	}
}e[200005];
int getf(int v,int x)
{
	if (fa[v][x]==v) return fa[v][x];
	else return fa[v][x]=getf(fa[v][x],x);
}
void merge(int x,int y,int p)
{
	x=getf(x,p),y=getf(y,p);
	if (size[x][p]>size[y][p]) swap(x,y);
	fa[x][p]=y;
	size[y][p]+=size[x][p];
}
bool check(int x,int y,int p)
{
	x=getf(x,p),y=getf(y,p);
	return x==y;
}
signed main()
{
	scanf("%lld%lld%lld%lld",&n,&m,&p,&q);
	for (int i=1;i<=p;i++)
	{
		scanf("%lld%lld%lld",&u,&v,&w);
		e[++cnt].sta=u;
		e[cnt].to=v;
		e[cnt].val=w;
		e[cnt].flag=1; 
		ans+=w*n;
	}
	for (int j=1;j<=q;j++)
	{
		scanf("%lld%lld%lld",&u,&v,&w);
		e[++cnt].sta=u;
		e[cnt].to=v;
		e[cnt].val=w;
		e[cnt].flag=0;
		ans+=w*m;
	}
	for (int i=1;i<=n;i++)
		fa[i][0]=i,size[i][0]=1;
	for (int i=1;i<=m;i++)
		fa[i][1]=i,size[i][1]=1;
	sort(e+1,e+1+cnt);
	int chosen=0,i=1,tn=n,tm=m;
	while (chosen<tn*tm-1)
	{
		int u=e[i].sta,v=e[i].to,w=e[i].val,f=e[i].flag;
		if (!check(u,v,f))
		{
			merge(u,v,f);
			if (!f) ans-=w*m,n--,chosen+=m;
			else ans-=w*n,m--,chosen+=n;
		}
		i++;
	}
	printf("%lld",ans);
	return 0;
}