卷积(转自wiki百科)
-
维基百科,自由的百科全书
图示两个方形脉冲波的卷积。其中函数 "g" 首先对
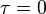 反射,接着平移 "t" ,成为
反射,接着平移 "t" ,成为 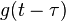 。那么重叠部份的面积就相当于 "t" 处的卷积,其中横坐标代表待积变量
。那么重叠部份的面积就相当于 "t" 处的卷积,其中横坐标代表待积变量  以及新函数
以及新函数 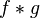 的自变量 "t" 。
的自变量 "t" 。图示方形脉冲波和指数衰退的脉冲波的卷积(后者可能出现于 RC电路中),同样地重叠部份面积就相当于 "t" 处的卷积。注意到因为 "g" 是对称的,所以在这两张图中,反射并不会改变它的形状。
在泛函分析中,卷积(捲積)、旋積或摺積,是通过两个函数f 和g 生成第三个函数的一种数学算子,表征函数f 与经过翻转和平移的g 的重叠部分的累积。如果将参加卷积的一个函数看作区间的指示函数,卷积还可以被看作是“滑动平均”的推广。
目录
简单介绍
卷积是分析数学中一种重要的运算。设:
 ,
, 是
是 上的两个可积函数,作积分:
上的两个可积函数,作积分:可以证明,关于几乎所有的
 ,上述积分是存在的。这样,随着
,上述积分是存在的。这样,随着  的不同取值,这个积分就定义了一个新函数
的不同取值,这个积分就定义了一个新函数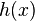 ,称为函数
,称为函数 与
与 的卷积,记为
的卷积,记为 。我们可以轻易验证:
。我们可以轻易验证: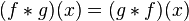 ,并且
,并且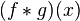 仍为可积函数。这就是说,把卷积代替乘法,
仍为可积函数。这就是说,把卷积代替乘法, 空间是一个代数,甚至是巴拿赫代数。
空间是一个代数,甚至是巴拿赫代数。卷积与傅里叶变换有着密切的关系。例如两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换,利用此一性质,能简化傅里叶分析中的许多问题。
由卷积得到的函数
 一般要比
一般要比  和
和  都光滑。特别当
都光滑。特别当  为具有紧支集的光滑函数,
为具有紧支集的光滑函数, 为局部可积时,它们的卷积
为局部可积时,它们的卷积  也是光滑函数。利用这一性质,对于任意的可积函数
也是光滑函数。利用这一性质,对于任意的可积函数  ,都可以简单地构造出一列逼近于
,都可以简单地构造出一列逼近于  的光滑函数列
的光滑函数列  ,这种方法称为函数的光滑化或正则化。
,这种方法称为函数的光滑化或正则化。卷积的概念还可以推广到数列、测度以及广义函数上去。
定义
函数f 与g 的卷积记作
 ,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。
,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。积分区间取决于f 与g 的定义域。
对于定义在离散域的函数,卷积定义为
图解卷积
- 首先将两个函数都用
 来表示。
来表示。 - 对其中一个函数做水平翻转:
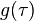 →
→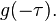
- 加上一个时间偏移量,让
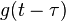 能沿着
能沿着  轴滑动。
轴滑动。 - 让t从-∞滑动到+∞。两函数交会时,计算交会范围中两函数乘积的积分值。换句话说,我们是在计算一个滑动的的加权平均值。也就是使用
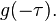 当做加权函数,来对
当做加权函数,来对 取加权平均值。
取加权平均值。
- 最后得到的波形(未包含在此图中)就是f和g的卷积。
如果f(t)是一个单位脉冲,我们得到的乘积就是g(t)本身,称为冲激响应 。
计算卷积的方法
当
![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 为有限长度
为有限长度  ,
, ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 为有限长度
为有限长度  的信号,计算卷积
的信号,计算卷积 ![卷积 f[n]*g[n]](http://upload.wikimedia.org/math/7/4/6/746f8c01c58a4172f70d46920d3f5fc4.png) 有三种主要的方法,分别为 1.直接计算(Direct Method) 2.快速傅里叶转换(FFT) 和 3.分段卷积 (sectioned convolution)。方法1是直接利用定义来计算卷积,而方法2和3都是用到了FFT来快速计算卷积。也有不需要用到FFT的作法,如使用数论转换。
有三种主要的方法,分别为 1.直接计算(Direct Method) 2.快速傅里叶转换(FFT) 和 3.分段卷积 (sectioned convolution)。方法1是直接利用定义来计算卷积,而方法2和3都是用到了FFT来快速计算卷积。也有不需要用到FFT的作法,如使用数论转换。方法1 直接计算
- 作法: 利用卷积的定义
- 若
![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 和
和 ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 皆为实数信号,则需要
皆为实数信号,则需要 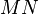 个乘法。
个乘法。
- 若
![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 和
和 ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 皆为更一般性的复数信号,不使用复数乘法的快速算法,会需要
皆为更一般性的复数信号,不使用复数乘法的快速算法,会需要 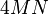 个乘法;但若使用复数乘法的快速算法,则可简化至
个乘法;但若使用复数乘法的快速算法,则可简化至 个乘法。
个乘法。
- 因此,使用定义直接计算卷积的复杂度为
 。
。
方法2 快速傅里叶转换(FFT)
- 概念:由于两个离散信号在时域(time domain)做卷积相当于这两个信号的离散傅里叶转换在频域(frequency domain)做相乘:
- ,可以看出在频域的计算较简单。
- 作法: 因此这个方法即是先将信号从时域转成频域:
- ,于是
- ,最后再将频域信号转回时域,就完成了卷积的计算:
- 总共做了 2 次 DFT 和 1 次 IDFT。
- 特别注意 DFT 和 IDFT 的点数
 要满足
要满足  。
。
- 由于 DFT 有快速算法 FFT,所以运算量为
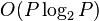
- 假设
 点 DFT 的乘法量为
点 DFT 的乘法量为  ,
,![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 和
和 ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 为一般性的复数信号,并使用复数乘法的快速算法,则共需要
为一般性的复数信号,并使用复数乘法的快速算法,则共需要 个乘法。
个乘法。
方法3 分段卷积(sectioned convolution)
- 概念: 将
![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 切成好几段,每一段分别和
切成好几段,每一段分别和 ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 做卷积后,再将结果相加。
做卷积后,再将结果相加。
- 作法: 先将
![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 切成每段长度为
切成每段长度为  的区段 (
的区段 ( ),假设共切成S段:
),假设共切成S段:
- Section 1:
![卷积 f_1[n] = f[n] , n=0,1,...,L-1](http://upload.wikimedia.org/math/0/0/0/0001578589109854144a23bffa2d3024.png)
- Section 1:
- Section 2:
![卷积 f_2[n] = f[n+L], n=0,1,...,L-1](http://upload.wikimedia.org/math/c/5/8/c58705cde5fd0b12e047eb6b312b5ff7.png)
- Section 2:
- Section r:
![卷积 f_r[n] = f[n+(r-1)L], n=0,1,...,L-1](http://upload.wikimedia.org/math/d/1/2/d12bf79f097273f64fc958a3fcc2c3eb.png)
- Section r:
- Section S:
![卷积 f_S[n] = f[n+(S-1)L], n=0,1,...,L-1](http://upload.wikimedia.org/math/e/a/c/eacee6d9f7935597431f204b2c1e57b7.png)
- Section S:
- ,
![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 为各个section的和
为各个section的和
- 因此,
,
- 每一小段作卷积则是采用方法2,先将时域信号转到频域相乘,再转回时域:
。
- 总共只需要做
 点 FFT
点 FFT  次,因为
次,因为 ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 只需要做一次FFT。
只需要做一次FFT。
- 假设
 点 DFT 的乘法量为
点 DFT 的乘法量为  ,
,![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 和
和 ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 为一般性的复数信号,并使用复数乘法的快速算法,则共需要
为一般性的复数信号,并使用复数乘法的快速算法,则共需要 个乘法。
个乘法。
- 运算量:
![卷积 \frac{N}{L}3(L+M-1)[\log_{2}(L+M-1)+1]](http://upload.wikimedia.org/math/e/a/c/eac14ef1c14e031b9c3e3328a1b91785.png)
- 运算复杂度:
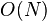 ,和
,和  呈线性,较方法2小。
呈线性,较方法2小。 - 分为 Overlap-Add 和 Overlap-Save 两种方法。
-
分段卷积: Overlap-Add
欲做
的分段卷积分,
长度为
,
长度为
,
Step 1: 将
每
分成一段
Step 2: 再每段
点后面添加
个零,变成长度
Step 3: 把
添加
个零,变成长度
的 h'[n]}
Step 4: 把每个 x[n]}
的小段和 h'[n]}
做快速卷积,也就是 IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h'[n])}\}}
,每小段会得到长度
的时域信号
Step 5: 放置第 i}
个小段的起点在位置 L\times i}
上, i=0,1,...,\lceil {\frac {N}{L}}\rceil -1}
Step 6: 会发现在每一段的后面 M-1}
点有重叠,将所有点都相加起来,顾名思义 Overlap-Add,最后得到结果
举例来说:
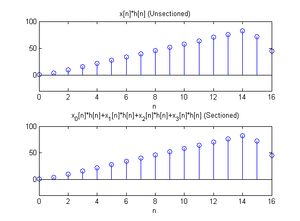
x[n]=[1,2,3,4,5,-1,-2,-3,-4,-5,1,2,3,4,5]}
, 长度 N=15}
h[n]=[1,2,3]}
, 长度 M=3}
令 L=5}
令 L=5}
切成三段,分别为 x_{0}[n],x_{1}[n],x_{2}[n]}
, 每段填 M-1}
个零,并将
填零至长度
将每一段做 IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h'[n])}\}}
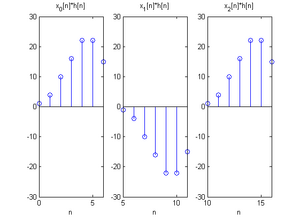
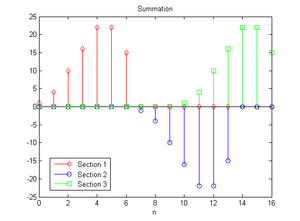
若将每小段摆在一起,可以注意到第一段的范围是 0\thicksim 6}
,第二段的范围是 5\thicksim 11}
,第三段的范围是 10\thicksim 16}
,三段的范围是有重叠的
最后将三小段加在一起,并将结果和未分段的卷积做比较,上图是分段的结果,下图是没有分段并利用快速卷积所算出的结果,验证两者运算结果相同。
分段卷积: Overlap-Save
欲做 x[n]*h[n]}
的分段卷积分, x[n]}
长度为 N}
,
长度为 M}
,
Step 1: 将 x[n]}
前面填 M-1}
个零
Step 2: 第一段 i=0}
, 从新的
中
取到
总共
点当做一段,因此每小段会重复取到前一小段的
点,取到新的一段全为零为止
Step 3: 把
添加 L-M}
个零,变成长度
的
Step 4: 把每个
的小段和
做快速卷积,也就是
,每小段会得到长度
的时域信号
Step 5: 对于每个小段,只会保留末端的
点,因此得名 Overlap-Save
Step 6: 将所有保留的点合再一起,得到最后结果
举例来说:
, 长度
, 长度
令
将
前面填
个零以后,按照 Step 2 的方式分段,可以看到每一段都重复上一段的
点
再将每一段做
以后可以得到
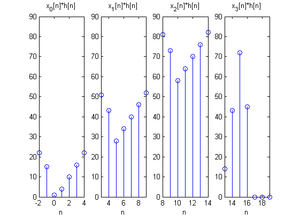
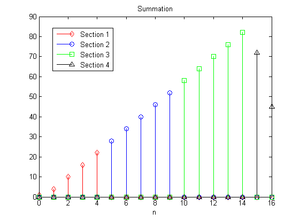
保留每一段末端的
点,摆在一起以后,可以注意到第一段的范围是
,第二段的范围是
,第三段的范围是}
,第四段的范围是
,四段的范围是没有重叠的
将结果和未分段的卷积做比较,下图是分段的结果,上图是没有分段并利用快速卷积所算出的结果,验证两者运算结果相同。
至于为什么要把前面 M-1}
丢掉?
以下以一例子来阐述:
, 长度
,
, 长度
,
第一条蓝线代表
轴,而两条蓝线之间代表长度
,是在做快速卷积时的周期
当在做快速卷积时
,是把信号视为周期
,在时域上为循环卷积分,
而在一开始前
点所得到的值,是
和
内积的值,
然而
这
个值应该要为零,以往在做快速卷积时长度为
时不会遇到这些问题,
而今天因为在做快速卷积时长度为
才会把这
点算进来,因此我们要丢弃这
点内积的结果
为了要丢弃这 M-1}
点内积的结果,位移 h[-n]}
M-1}
点,并把位移以后内积合的值才算有效。
应用时机
以上三种方法皆可用来计算卷积,其差别在于所需总体乘法量不同。基于运算量以及效率的考量,在计算卷积时,通常会选择所需总体乘法量较少的方法。
以下根据
![卷积 f[n]](http://upload.wikimedia.org/math/e/a/e/eaed2299febf5554577674f2ee2db3c2.png) 和
和 ![卷积 g[n]](http://upload.wikimedia.org/math/f/d/a/fda6cfe4e2697679d09b50bb47483a04.png) 的长度(
的长度(  )分成5类,并列出适合使用的方法:
)分成5类,并列出适合使用的方法: 为一非常小的整数 - 直接计算
为一非常小的整数 - 直接计算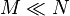 - 快速傅里叶转换
- 快速傅里叶转换 - 分段卷积
- 分段卷积 - 快速傅里叶转换
- 快速傅里叶转换 为一非常小的整数 - 直接计算
为一非常小的整数 - 直接计算
基本上,以上只是粗略的分类。在实际应用时,最好还是算出三种方法所需的总乘法量,再选择其中最有效率的方法来计算卷积。
例子
Q1: 当
 ,适合用哪种方法计算卷积?
,适合用哪种方法计算卷积?Ans:
- 方法1: 所需乘法量为

- 方法2:
 ,而2016点的DFT最少乘法数
,而2016点的DFT最少乘法数  ,所以总乘法量为
,所以总乘法量为 
- 方法3:
- 若切成 8 块(
 ),则
),则 。选
。选 ,则总乘法量为
,则总乘法量为  ,比方法1和2少了很多。
,比方法1和2少了很多。 - 但是若要找到最少的乘法量,必须依照以下步骤
- (1)先找出
 : 解
: 解  :
: ![卷积 \frac{\partial {\frac{N}{L}3(L+M-1)[\log_{2}(L+M-1)+1]}}{\partial L}=0](http://upload.wikimedia.org/math/5/6/9/569838cb35512e03528066a5304fc6e4.png)
- (2)由
 算出点数在
算出点数在  附近的DFT所需最少的乘法量,选择DFT的点数
附近的DFT所需最少的乘法量,选择DFT的点数 - (3)最后由
 算出
算出 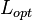
- (1)先找出
- 因此,
- (1)由运算量对
 的偏微分为0而求出
的偏微分为0而求出 
- (2)
 ,所以选择101点 DFT 附近点数乘法量最少的点数
,所以选择101点 DFT 附近点数乘法量最少的点数  或
或  。
。 - (3-1)当
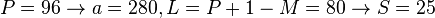 ,总乘法量为
,总乘法量为  。
。 - (3-2)当
 ,总乘法量为
,总乘法量为 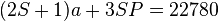 。
。
- (1)由运算量对
- 由此可知,切成 20 块会有较好的效率,而所需总乘法量为 21480。
- 若切成 8 块(
- 因此,当
 ,所需总乘法量: 分段卷积 < 快速傅里叶转换 < 直接计算。故,此时选择使用分段卷积来计算卷积最适合。
,所需总乘法量: 分段卷积 < 快速傅里叶转换 < 直接计算。故,此时选择使用分段卷积来计算卷积最适合。
Q2: 当
 ,适合用哪种方法计算卷积?
,适合用哪种方法计算卷积?Ans:
- 方法1: 所需乘法量为
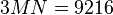
- 方法2:
 ,选择1026点 DFT 附近点数乘法量最少的点数,
,选择1026点 DFT 附近点数乘法量最少的点数,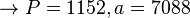 。
。- 因此,所需乘法量为
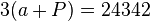
- 因此,所需乘法量为
- 方法3:
- (1)由运算量对
 的偏微分为0而求出
的偏微分为0而求出 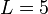
- (2)
 ,所以选择7点 DFT 附近点数乘法量最少的点数
,所以选择7点 DFT 附近点数乘法量最少的点数 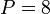 或
或 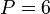 或
或 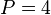 。
。 - (3-1)当
 ,总乘法量为
,总乘法量为  。
。 - (3-2)当
 ,总乘法量为
,总乘法量为 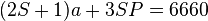 。
。 - (3-3)当
 ,总乘法量为
,总乘法量为  。
。
- (1)由运算量对
- 由此可知,切成 171 块会有较好的效率,而所需总乘法量为 5476。
- 因此,当
 ,所需总乘法量: 分段卷积 < 直接计算 < 快速傅里叶转换。故,此时选择使用分段卷积来计算卷积最适合。
,所需总乘法量: 分段卷积 < 直接计算 < 快速傅里叶转换。故,此时选择使用分段卷积来计算卷积最适合。 - 虽然当
 是个很小的正整数时,大致上适合使用直接计算。但实际上还是将3个方法所需的乘法量都算出来,才能知道用哪种方法可以达到最高的效率。
是个很小的正整数时,大致上适合使用直接计算。但实际上还是将3个方法所需的乘法量都算出来,才能知道用哪种方法可以达到最高的效率。
Q3: 当
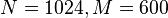 ,适合用哪种方法计算卷积?
,适合用哪种方法计算卷积?Ans:
- 方法1: 所需乘法量为

- 方法2:
 ,选择1026点 DFT 附近点数乘法量最少的点数,
,选择1026点 DFT 附近点数乘法量最少的点数, 。
。- 因此,所需乘法量为

- 因此,所需乘法量为
- 方法3:
- (1)由运算量对
 的偏微分为0而求出
的偏微分为0而求出 
- (2)
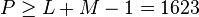 ,所以选择1623点 DFT 附近点数乘法量最少的点数
,所以选择1623点 DFT 附近点数乘法量最少的点数  。
。 - (3)当
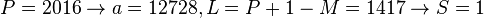 ,总乘法量为
,总乘法量为 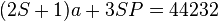 。
。
- (1)由运算量对
- 由此可知,此时切成一段,就跟方法2一样,所需总乘法量为 44232。
- 因此,当
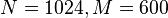 ,所需总乘法量: 快速傅里叶转换 = 分段卷积 < 直接计算。故,此时选择使用分段卷积来计算卷积最适合。
,所需总乘法量: 快速傅里叶转换 = 分段卷积 < 直接计算。故,此时选择使用分段卷积来计算卷积最适合。
多元函数卷积
按照翻转、平移、积分的定义,还可以类似的定义多元函数上的积分:
性质
各种卷积算子都满足下列性质:
其中Df 表示f的微分,如果在离散域中则是指差分算子,包括前向差分与后向差分两种:
- 前向差分:
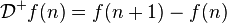
- 后向差分:
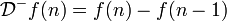
卷积定理
卷积定理指出,函数卷积的傅里叶变换是函数傅里叶变换的乘积。即,一个域中的卷积相当于另一个域中的乘积,例如时域中的卷积就对应于频域中的乘积。
其中
 表示f 的傅里叶变换。
表示f 的傅里叶变换。这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、Mellin变换和Hartley变换(参见Mellin inversion theorem)等各种傅里叶变换的变体同样成立。在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。
利用卷积定理可以简化卷积的运算量。对于长度为
 的序列,按照卷积的定义进行计算,需要做
的序列,按照卷积的定义进行计算,需要做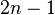 组对位乘法,其计算复杂度为
组对位乘法,其计算复杂度为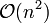 ;而利用傅里叶变换将序列变换到频域上后,只需要一组对位乘法,利用傅里叶变换的快速算法之后,总的计算复杂度为
;而利用傅里叶变换将序列变换到频域上后,只需要一组对位乘法,利用傅里叶变换的快速算法之后,总的计算复杂度为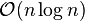 。这一结果可以在快速乘法计算中得到应用。
。这一结果可以在快速乘法计算中得到应用。在群上的卷积
若 G 是有某 m 测度的群(例如豪斯多夫空间上哈尔测度下局部紧致的拓扑群),对于G 上 m-勒贝格可积的实数或复数函数f 和g,可定义它们的卷积:
对于这些群上定义的卷积同样可以给出诸如卷积定理等性质,但是这需要对这些群的表示理论以及调和分析的彼得-外尔定理。
应用
卷积在工程和数学上都有很多应用:
- 统计学中,加权的滑动平均是一种卷积。
- 概率论中,两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。
- 声学中,回声可以用源声与一个反映各种反射效应的函数的卷积表示。
- 电子工程与信号处理中,任一个线性系统的输出都可以通过将输入信号与系统函数(系统的冲激响应)做卷积获得。
- 物理学中,任何一个线性系统(符合叠加原理)都存在卷积。
参见
外部链接
- PlanetMath上Convolution的资料。
- Visual convolution Java Applet
- Lecture notes, Jian-Jiun Ding (2013), Advanced Digital Signal Processing





![卷积 (f * g)[m] = \sum_n {f[n] g[m - n]}](http://upload.wikimedia.org/math/8/7/d/87d76adca3c545f6832302da3f434c38.png)

![卷积 y[n] = f[n]*g[n] = \sum_{m=0}^{M-1} f[n-m]g[m]](http://upload.wikimedia.org/math/d/3/2/d32d180c50e94b71b39401982d4ef5b4.png)















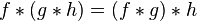

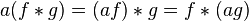


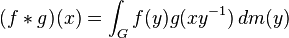

 浙公网安备 33010602011771号
浙公网安备 33010602011771号