1588. 所有奇数长度子数组的和
题目1588. 所有奇数长度子数组的和
给你一个正整数数组 arr ，请你计算所有可能的奇数长度子数组的和。
子数组 定义为原数组中的一个连续子序列。
请你返回 arr 中 所有奇数长度子数组的和 。
示例 1：
输入：arr = [1,4,2,5,3]
输出：58
解释：所有奇数长度子数组和它们的和为：
[1] = 1
[4] = 4
[2] = 2
[5] = 5
[3] = 3
[1,4,2] = 7
[4,2,5] = 11
[2,5,3] = 10
[1,4,2,5,3] = 15
我们将所有值求和得到 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
示例 2：
输入：arr = [1,2]
输出：3
解释：总共只有 2 个长度为奇数的子数组，[1] 和 [2]。它们的和为 3 。
示例 3：
输入：arr = [10,11,12]
输出：66
提示：
1 <= arr.length <= 100
1 <= arr[i] <= 1000
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sum-of-all-odd-length-subarrays
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
解法
1、kadane 算法原理
用 Excel 表格展示这个二维 kadane 算法的过程。
如图下面所示的矩阵，黄色黄色部分，4×54×5 的大小。先定义几个变量：
1. 变量 LL : 代表遍历时，当前子矩阵的左边位置；
2. 变量 RR : 代表遍历时，当前子矩阵的右边位置；
3. 右边浅绿色，与矩阵的 row数row数 相同的临时存储区，是将当前的 LL 列、L+1L+1 列、……、R−1R−1 列、RR 列，进行列相加，然后再用 kadane 算法判断相加得到的列数组（此时即为一维数组了，可以用一般意义上的 kadane 算法），求此时元素连续和最大的子数组，并与之前的最大值进行比较（这一点会在下面的过程中体现出来）；
4. 变量 currentSumcurrentSum : 当前 L、RL、R 组成的子矩阵（注意：这个子矩阵的“行数量“与原来大矩阵相同），其中这个矩阵的子矩阵，产生的最大的和；
5. 变量 maxSummaxSum : 纪录目前遍历下来的最大的子矩阵和；
6. 变量 maxLeftmaxLeft : 纪录目前遍历下来的最大子矩阵的左边位置；
7. 变量 maxRightmaxRight : 纪录目前遍历下来的最大子矩阵的右边位置；
8. 变量 maxUpmaxUp : 纪录目前遍历下来的最大子矩阵的上面位置；
9. 变量 maxDownmaxDown : 纪录目前遍历下来的最大子矩阵的下面位置；
注意：如果 currentSumcurrentSum 不大于 maxSummaxSum，则保持 maxSum、maxLeft、maxRight、maxUp、maxDownmaxSum、maxLeft、maxRight、maxUp、maxDown 这几个变量值不变。
第一次遍历，L、RL、R 都在矩阵的开始 0 处：
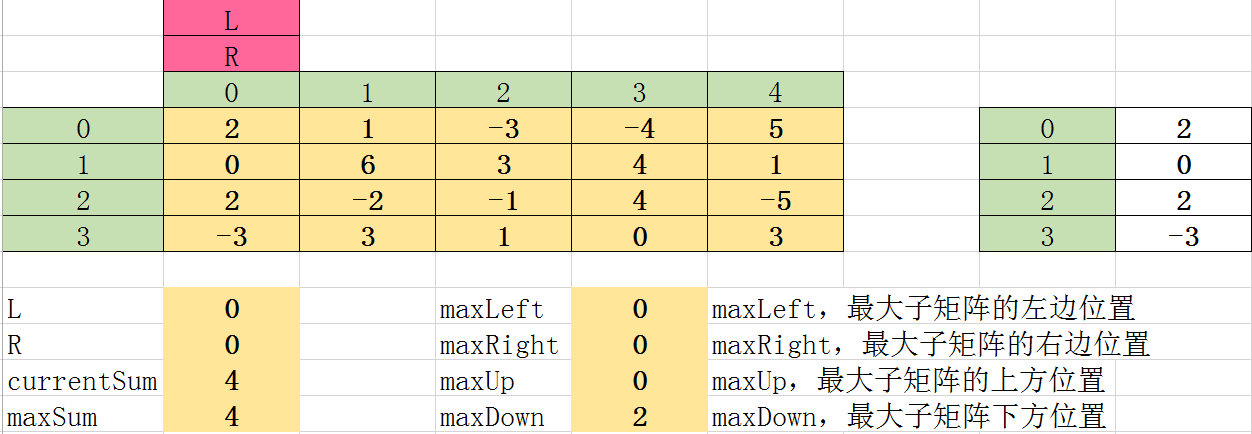
第二次遍历， 此时将 RR 向右移动一个位置到 1 处，保持 LL 位置不变。将 L、RL、R 两行之间的矩阵进行列相加，得到 3 6 0 0，求这个 3 6 0 0序列的和最大子序列。
很容易看出，最大值为9，所以 currentSumcurrentSum 为9，那么发现9比之前的 maxSum=4maxSum=4 要大，所以，此时将 9 给 maxSum=9maxSum=9。maxLeft=0maxLeft=0 纪录此时的 L=0L=0，maxRight=1maxRight=1 纪录此时的 R=1R=1，maxUpmaxUp 纪录此时最大子序列的上面开始位置：maxUp=0maxUp=0，maxDownmaxDown 纪录此时最大子序列的下面结束位置：maxDown=1maxDown=1：
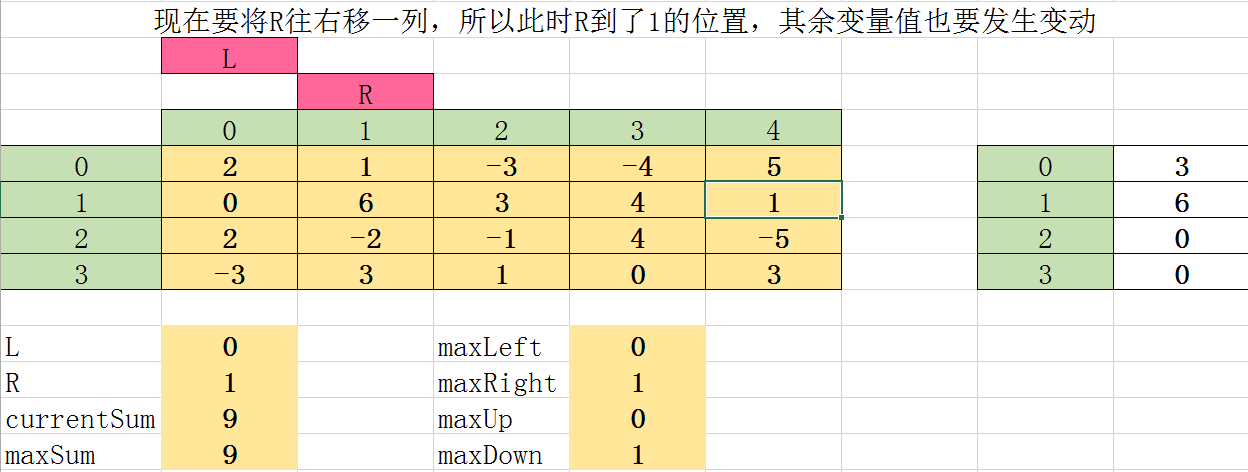
第三次遍历：
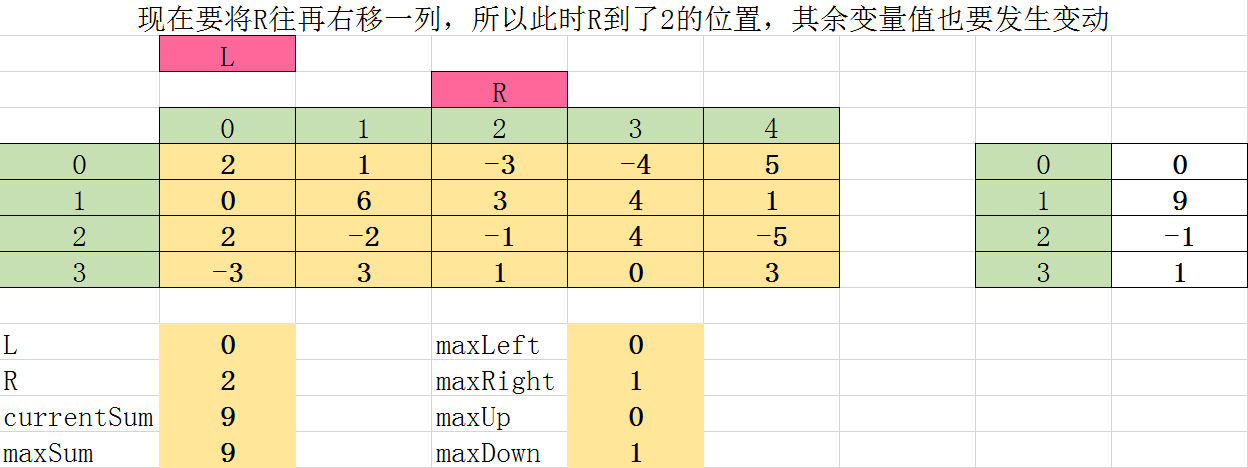
第四次遍历：
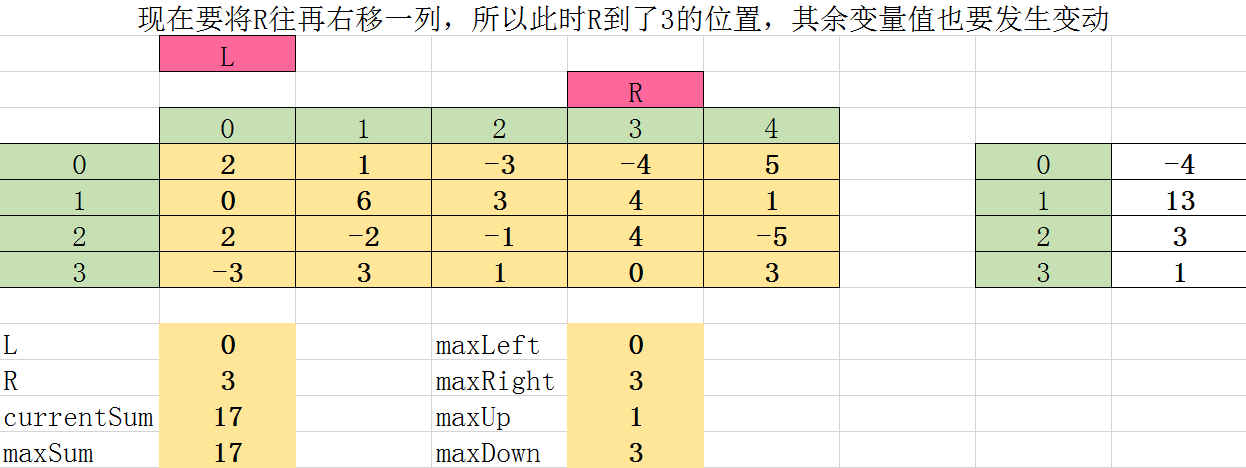
第五次遍历：
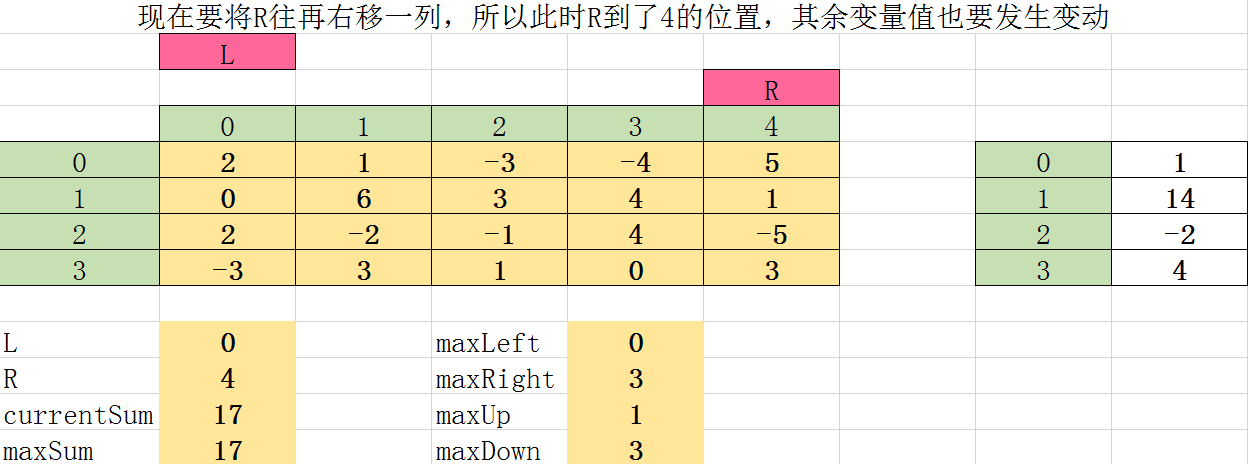
第六次遍历：
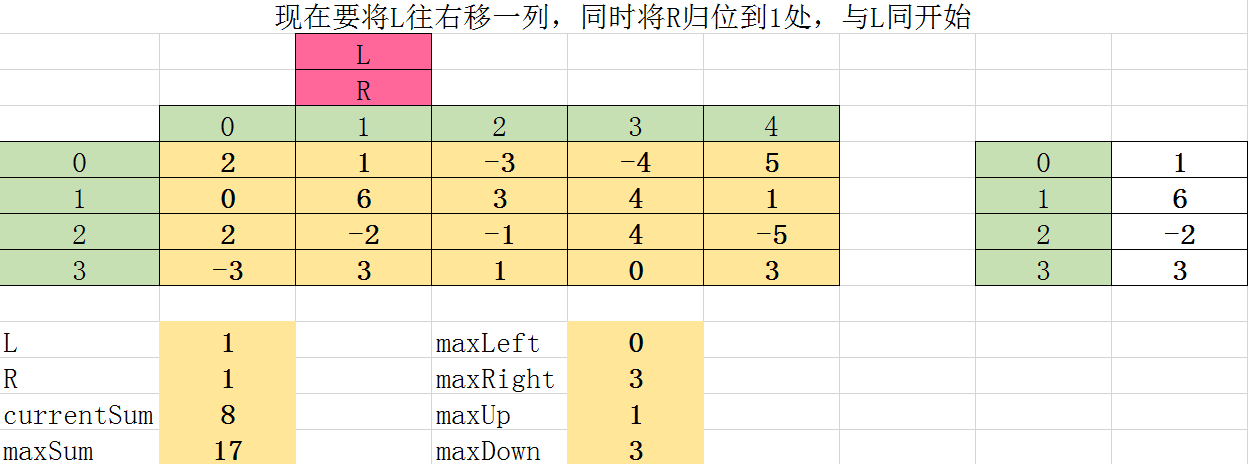
第七次遍历：
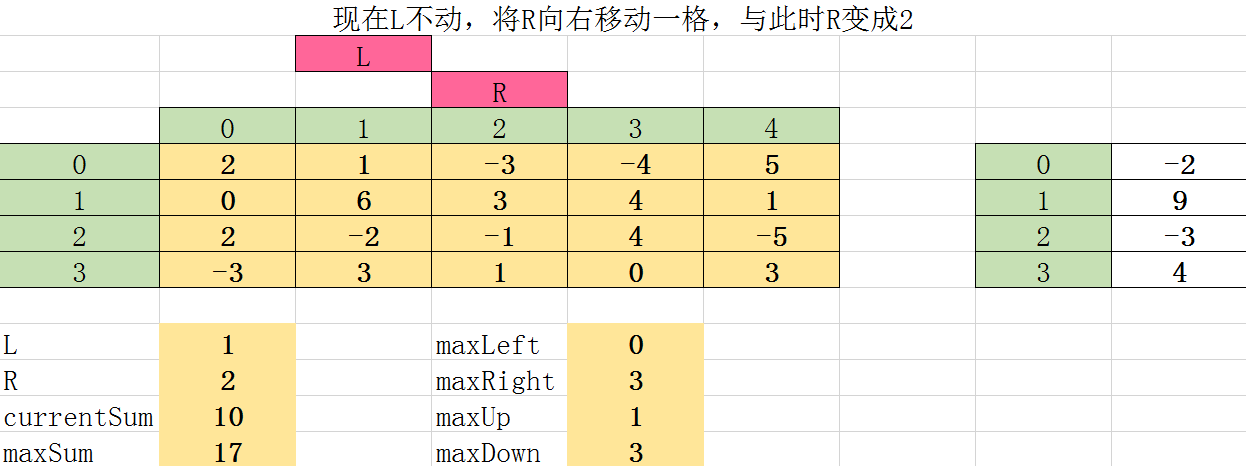
第八次遍历：
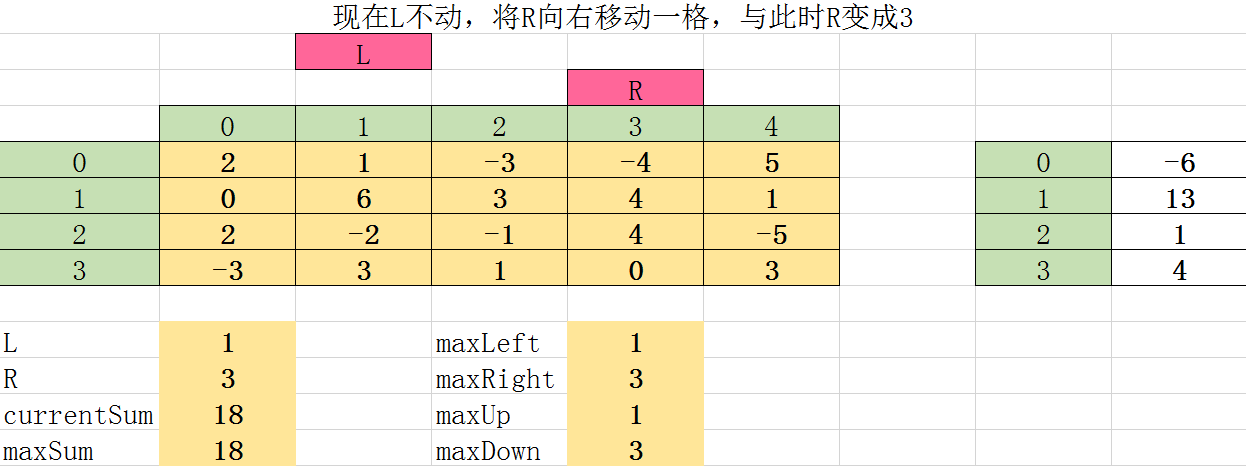
第九次遍历：
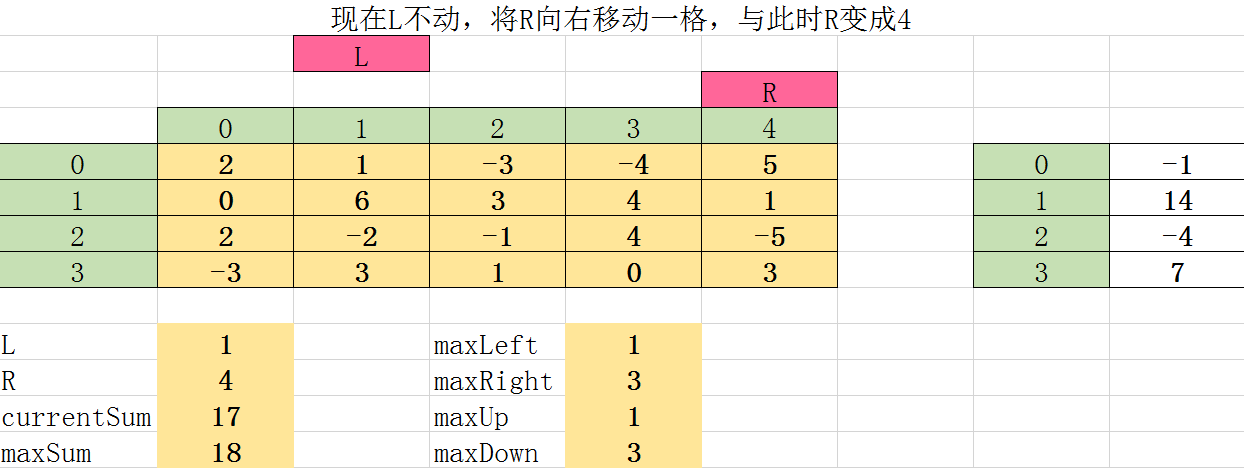
第十次遍历：
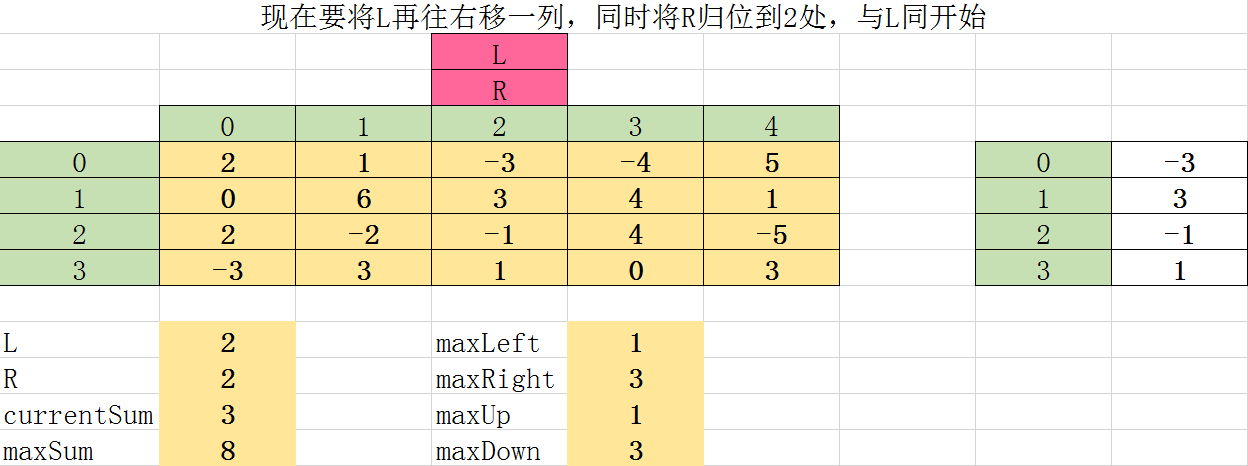
第十一次遍历：
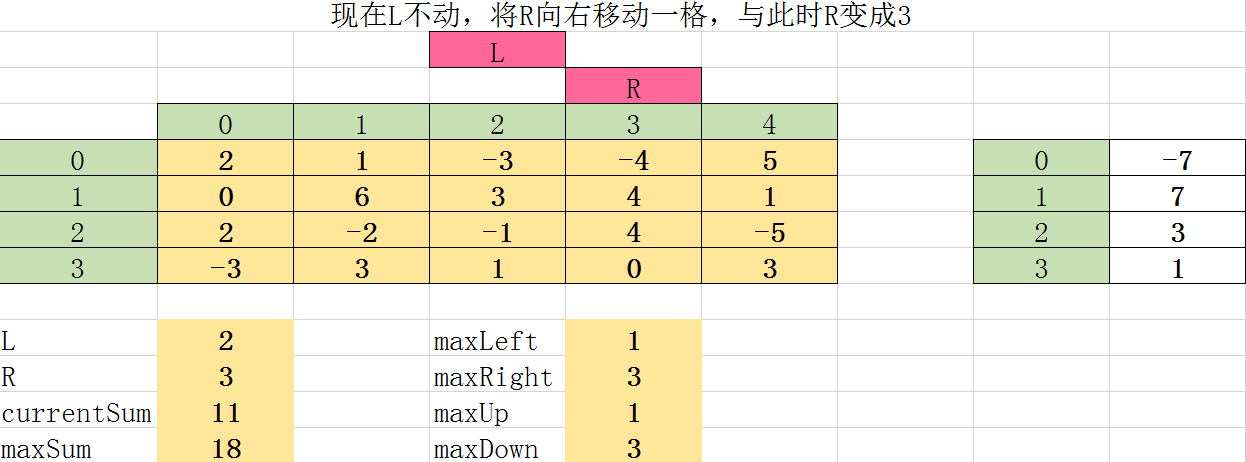
第十二次遍历：
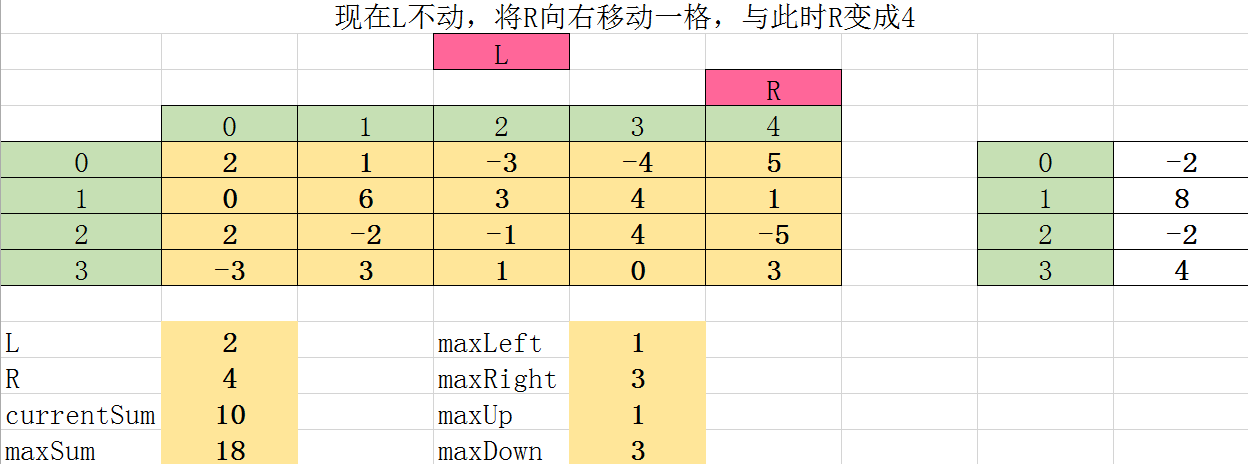
第十三次遍历：
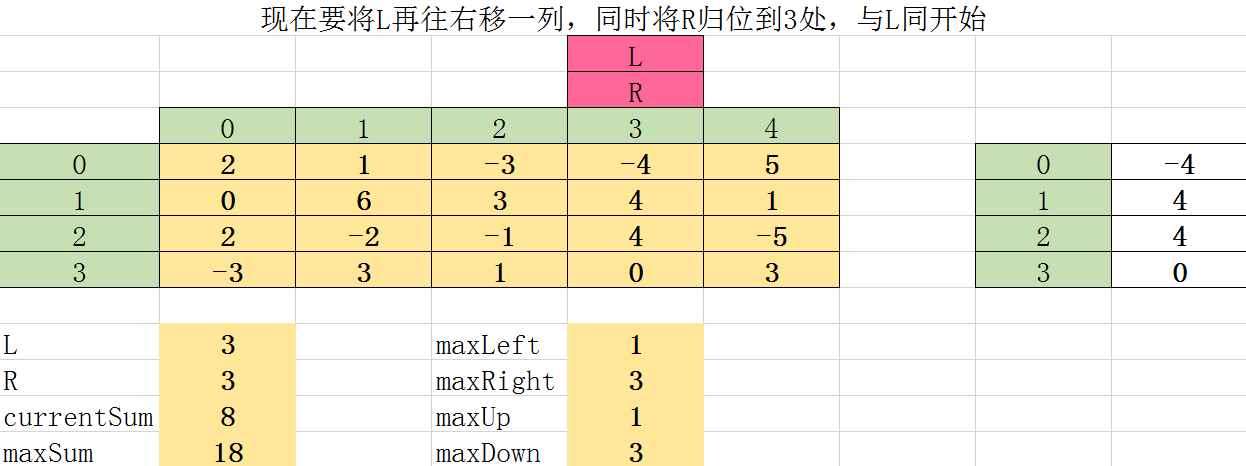
第十四次遍历：
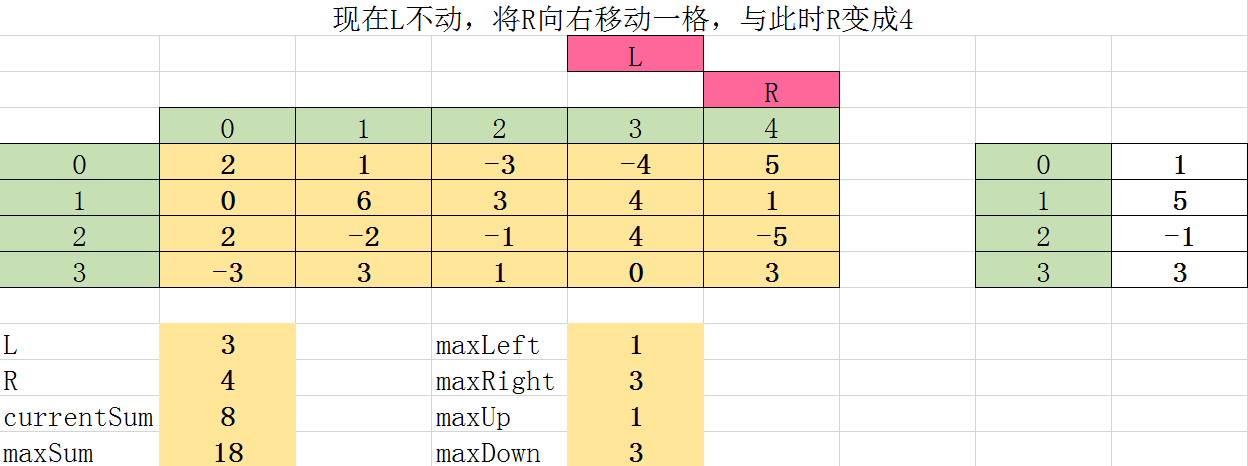
第十五次遍历：
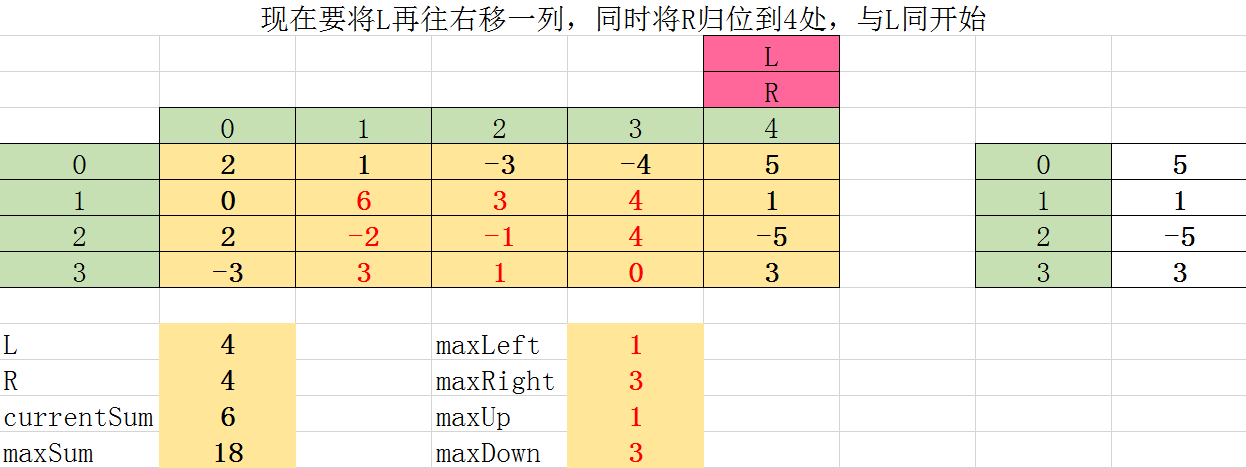
经过十五次的遍历后，我们终于找到了这个矩阵，就是上图中红色区域部分。这个大矩阵（4×54×5） 的最大元素和为18。
这就是2D kadane算法的过程。这个算法的空间复杂度为: O(row)O(row)，时间复杂度为：O(column×column×row)
2、kadane 算法源码
