[基础]斯坦福cs231n课程视频笔记(二) 神经网络的介绍

目录

• Introduction to Neural Networks
  • BP
  • Nerual Network
  • Convolutional Neural Network

Introduction to Neural Networks

BP

梯度反向传播BackPropagation，是神经网络中的重要算法，主要思想是：

• 计算网络的输出与期望输出之间的误差

• 将误差从网络的输出层回传，沿着网络逐层传递，传递的是损失值相对当前层里参数的梯度

• 当每一层都接收到该层的参数梯度时，沿着梯度方向更新参数

• 用更新后的网络参数来计算新的输出，再重新计算误差，误差梯度回传，循环上述过程直到参数收敛

\

结合计算图来理解：

computation graph 计算图

任何函数都可以拆成计算图的形式

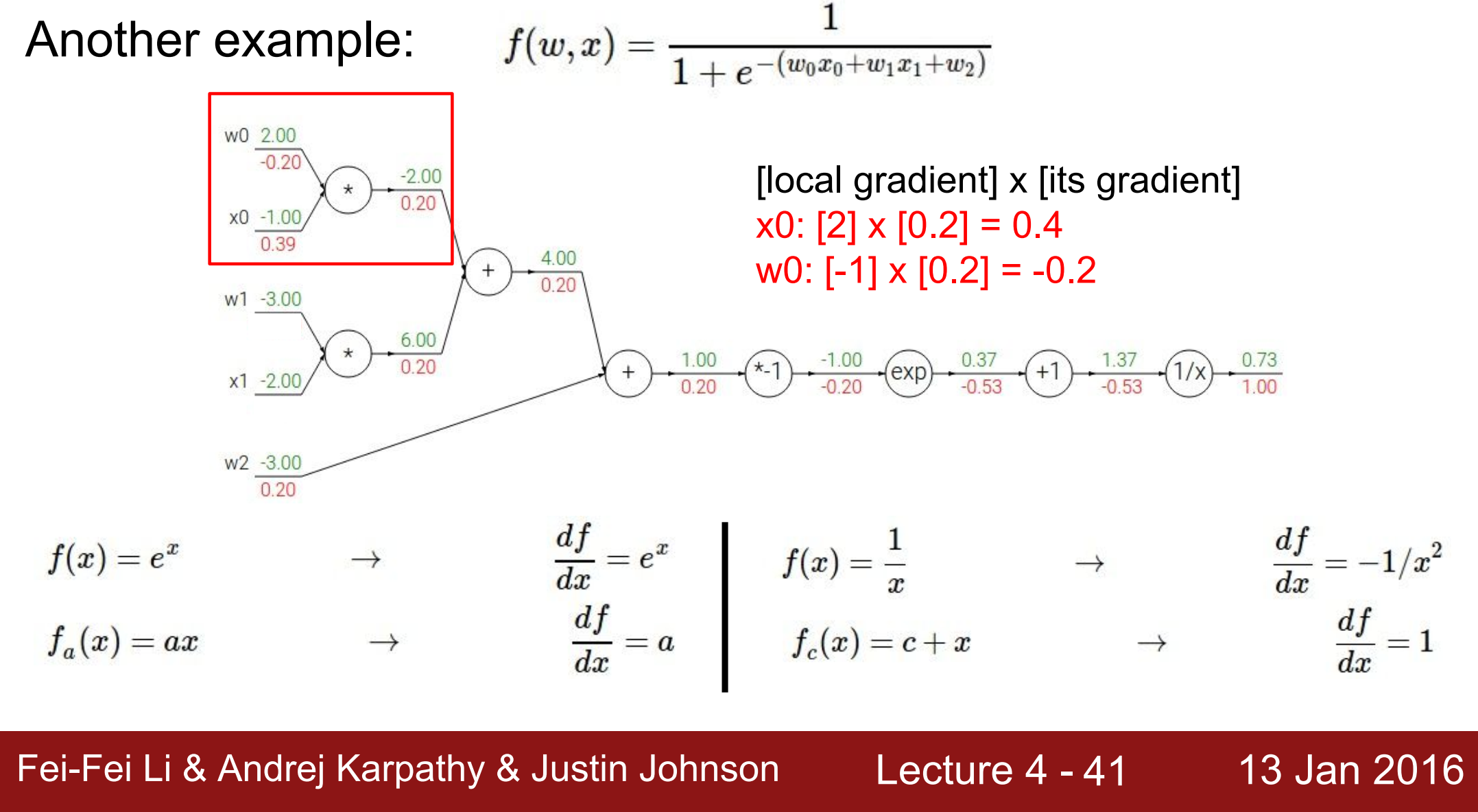
绿色的部分，是每个计算节点的输入值和输出值，即forward pass

红色的部分，是网络最终输出对于每个节点的梯度= local gradient * 前一个节点的梯度，即backward pass

• 最终输出的节点
  \[\frac{\partial f}{\partial f} = 1 \]

• 对前一个节点的梯度：记 $f = \frac{1}{z} $ (z为中间变量的名称)，
  \[\frac{\partial f}{\partial z} = \frac{\partial f}{\partial f} * \frac{\partial f}{\partial z} = 1 * \frac{-1}{1.37^2} =-0.53 \]

• 对倒数第二个节点的梯度：记 $z = h+1 $，
  \[\frac{\partial f}{\partial h} = \frac{\partial f}{\partial z} * \frac{\partial z}{\partial h} = -0.53*1 =-0.53 \]

• 对倒数第三个节点的梯度：记 \(h = e^m\) ，
  \[\frac{\partial f}{\partial m} = \frac{\partial f}{\partial h} * \frac{\partial h}{\partial m} = -0.53*e^{-1} =-0.20 \]

将一维推广到多维，现在假设W是 2 * 2，x是 2 维向量

\

【注意】

在全连接网络Fully Connected Network中，做反向传播时，误差对偏置bias的求导，需要对所有样本求和，这是因为loss就是对所有样本求和的结果，简单推理如下：

\[shape \ of\ x:(N,D),\ shape\ of\ w:(D,), \ shape \ of \ b:(D,) \\ loss = \sum_{i=1}^N L_i \ , loss \ is \ a \ constant \\ d\ scores = \frac{d\ loss}{d\ scores} \ , shape \ is\ (N,D) \\ scores = wx + b \\ d\ b_j = \frac{d\ loss_j}{d\ b_j} = \frac{d\ loss}{d\ scores} * \frac{d\ scores}{d\ b} =\sum_i^N d\ scores_{ij} \\ <=> d\ b_j = \frac{d\ scores_{1j}+d\ scores_{2j}+...}{d\ b_j} \\ (d\ loss_j = \sum_i^N L_{ij} ) \]

Nerual Network

​ neural network are a class of functions where we have simpler functions that are stacked on top of each other with non-linear functions in-between.. and we stacked them in a hierarchical way in order to make up a more complex non-linear function

可以看做是线性函数的叠加，同时线性函数层之间还夹杂着非线性层，来使网络具有非线性

• 如果单纯全是线性层的话，网络的代表能力会比较差 即难以表示复杂的变化：想象一下 多个线性函数的叠加在一起得到的也是线性函数 而线性函数的表达能力比较差 比如二维坐标系x-y下的线性函数只是一条直线，当特征产生一些变化 输出必须随之变化
  \

网络中不同线性函数层是在提取不同层次的特征，网络中较低的层提取低层的语义特征，越高层提取到的特征越抽象。比如：

• 网络有两层线性函数层，对于输入图像，第一层的特征(or templates)有专门检测左侧人脸的滤波器，和检测右侧人脸的滤波器；而第二层特征是对第一层提取出来的特征做weighted sum 可以理解为第二层的特征有专门检测人脸的滤波器
• 如果输入图像是左侧人脸，那么经过第一层特征提取之后，检测左侧人脸滤波器得到的结果(score)比检测右侧人脸滤波器得到的结果高，然后输入到第二层，经过第二层的特征提取之后，在检测人脸的滤波器得到的结果(score)比在检测车的滤波器得到的结果高，第二层的输出即为网络的输出。
• 如果输入图像是正面人脸，那么经过第一层，左侧人脸滤波器得到的结果可能大致等于右侧人脸滤波器的结果，而经过第二层之后，得到的输出仍然也是人脸的可能性高于车辆。

\

Convolutional Neural Network

参见之前的博文

\