[基础]Deep Learning的基础概念

目录

• DNN
• CNN
  • DNN VS CNN
    • Example
  • 卷积的好处why convolution?
    • • 权值共享 parameter sharing
      • 稀疏连接 sparse connection
      • 平移不变性
• DCNN
  • 卷积核移动的步长 stride
  • 激活函数 active function
  • 通道 channel
  • 补零 padding
  • 参数计算
  • 池化层 Pooling layer
    • 池化层的超参数：
    • 池化层的类型：
  • 全连接层 Fully connected layer FC层
  • CNN的一些性质
    • 不变性 invariant
      • 平移不变性　translation invariant
      • 旋转不变性 和 缩放（尺度）不变性
    • 反向传播梯度消失
  • 常规框架
  • trick
    • #空洞卷积 dialted convolution
    • #随机丢弃 dropout
    • #批正则化 Batch Normalization
    • #迁移学习 transfer learning
    • #数据增强 data augmentation
      • tips for doing well on benchmarks/winning competitions
  • 参考资料：

DNN

Deep Neural Network == feed-forward-network == multilayer perceptron(MLP)

input -> 一系列全连接层 -> output

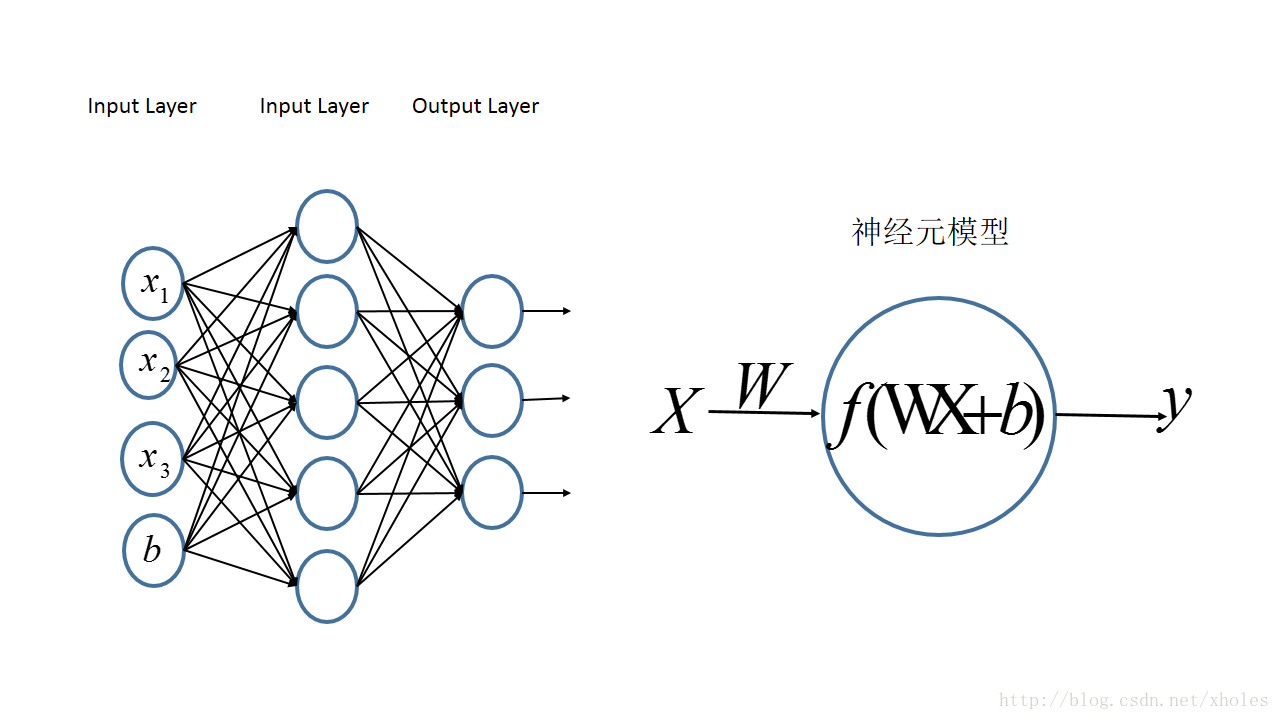
CNN

【注意】 深度学习中的卷积操作和信号处理里面的不一样，信号处理或是数学课本上说的卷积，需要先对卷积核做关于中心的翻转然后再对应元素相乘相加；而不翻转 直接对应元素相乘相加的操作叫相关 cross-corelation。在深度学习中是直接用卷积核和图像的对应元素相乘相加，其实是做的相关操作，但称作卷积。

DNN VS CNN

Deep Neural Network, feed-forward-network ,also known as a multilayer perceptron

• 有一系列全连接层在中间

Convolutional Neural Network

• 用卷积对图像做操作，将所使用的卷积核看做未知参数，在训练网络的过程中求出最优参数，具体参见下文DCNN的图

Example

以数字手写体识别为例

• 对于反馈前向网络(DNN)，需要将4 * 4的2D图像拉伸成1D的长度是16 * 1 的向量，才能作为网络的输入。

  拉伸使得原本2D图像中像素之间的位置信息丢失，只留下每个像素的灰度值，难以正确识别出数字

• 对于卷积神经网络，卷积层在2D图像上定义了窗口的概念，用窗口去框出图像的一部分区域，在这部分区域上和窗口进行卷积操作，得出的结果填入到输出图像的对应位置，然后通过逐步地平移窗口来扫描整个图像。窗口window也叫滤波器filter\卷积核kernel。

  • 通过设置特定的窗口参数值来搜寻一些特定的特征(比如边缘)

    扫描数字'4'，可以定义专门检测水平直线的窗口和检测垂直直线的窗口。

  • 窗口扫描过整个图像后输出的结果称作特征图 feature map，feature map一般比原图的尺寸小，如果想和原图的尺寸保持一致，可以在原图的四周根据窗口的尺寸进行补零padding。

  并不是所有的窗口都适用于检测数字'4'，比如用检测右对角线的窗口则没有什么效果。一般实际应用中并不会直接指定窗口的参数值，而是设置参数变量，在训练过程中让网络去学习最优的参数值。

  我们可以将多层卷积层stack together(叠在一起)，即对于卷积的结果继续卷积。

卷积的好处why convolution?

权值共享 parameter sharing

• 理由：a feature detector(such as edge detector) that's useful in one part of the image is probably useful in another part of image.
• 好处：减少参数个数（相比起传统的多层感知机模型，假如第一层图像是n1 * n1 * c1 ，第二层图像是 n2 * n2 * c2，对于感知机模型，需要在第一层有n1 * n1 * c1，第二层有n2 * n2 * c2个神经元，然后将它们全连接，参数个数即权重个数非常多 ，而如果是用卷积的操作，参数个数就是所有卷积核的总元素个数+偏置个数 ）

稀疏连接 sparse connection

• 含义：卷积之后的每个元素只和原图中对应的周围区域有关，而与其他区域无关

因此由于上述两个机制，卷积神经网络的参数个数比较少(相对于DNN这种全连接网络来说)，从而降低过拟合的概率

平移不变性

下文有提及

DCNN

Deep Convolutional Neural Network 更深的CNN (下面把DCNN都称为CNN)

Example

识别正方形，可以考虑 边特征和角特征，正方形有两对长度相等的平行边{A1,A2,B1,B2}，两两的夹角是直角。因此是用低层次的特征来描述高层次的物体。

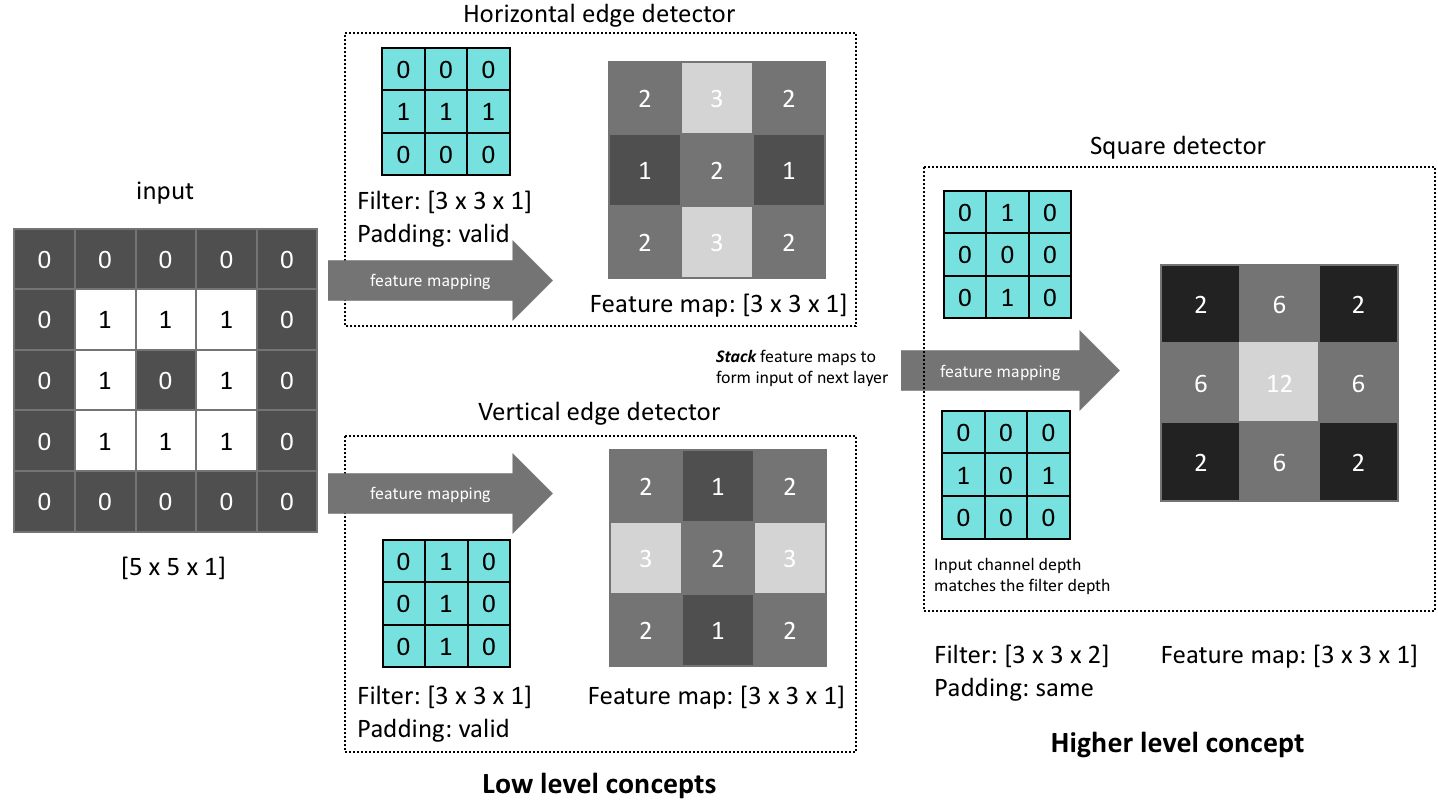
如何卷积？将卷积核(filter)的3 * 3 区域放到图像中，遍历(scan)整个图像，每次将卷积核和图像的某个3 * 3区域 元素相乘，得到的结果填到输出图像的相应位置

每次卷积之前对输入图像补零；图像尺寸的格式为 长 * 宽 * 通道个数

第一层的输入图像是 5 * 5 * 1，用两个卷积核，尺寸分别都为 3 * 3 * 1，得到两张特征图

卷积之后输出图像是 3 * 3 * 2，通道数为2，每个通道分别代表一个卷积核得到的特征图

然后将每个特征图里的每个元素加上偏置之后，传给非线性激活函数，ReLU(x+b)，偏置的下标和特征图(即通道个数)一致，即一张特征图对应一个偏置b。这样之后形成新的特征图，作为第二层的输入。

对应到多层感知机模型：

• 假设本层神经元的输入是\(a^{(0)}\) ，输出(即下一层神经元的输入)是 \(a^{(1)}\)
• 则 $a^{(1)} = f(w^{(0)} a^{(0)} + b) $ , \(f\) 是神经元的激活函数
• 则对输入图像执行卷积操作相当于 \(w^{(0)} a^{(0)}\) ，对形成的特征图加上偏置，再传给激活函数，得出输出。

第二层的输入图像是 3 * 3 * 2，用一个卷积核，尺寸为 3 * 3 * 2（因为卷积核的通道数要与输入图像保持一致）

第二层的输出图像是 3 * 3 * 1，将两个通道下的结果相加融合为1个通道（这是因为卷积核的通道数也为2所以对图像卷积就要相加）

卷积核移动的步长 stride

在上面的例子中，卷积核移动的步长为1，但实际情况中可以有多种选择，有时也会把步长定为2

• 卷积的步长决定了扫描整个图像所需的步数，即卷积后得到的特征图的size
• 某种程度上，是降采样方法
• 而作为同样是降采样方法的池化层，需要显式地定义出如何总结该窗口(summarize a window，比如需要定义是max pooling还是min还是average等等)

激活函数 active function

ReLU, sigmoid, tanh等等都是激活函数，在DNN(反馈前向网络)中也用到激活函数。

在CNN中，一般是紧跟在卷积层之后的处理，也就是：第n层卷积层 -> 激活函数 -> 第n+1层卷积层 -> 激活函数 -> 第n+2层卷积层 ....

如何在卷积层后用激活函数？将卷积后的图像里的每个像素都看做一个神经元节点，比如卷积后的特征图是 55 * 55 * 5，将每个元素(像素)都分别作为激活函数的输入，输出的结果形成新的图 55 * 55 * 5

通道 channel

https://blog.csdn.net/sscc_learning/article/details/79814146 更好地解释，可以认为是卷积核的个数

比如一个RGB图像的尺寸为 h * w * c，其中c=3 分别代表R\G\B三个通道。

卷积核与输入图像进行卷积时，要求卷积核的通道数必须与输入图像一致：

• 对于三通道的 h * w * 3，卷积核的尺寸为 f * f * 3，卷积后的结果是同一位置上三个通道相加的结果，因此卷积后的图只有1个通道

• 当一次使用多个卷积核时，比如用k个卷积核，则输出图像为 k 通道的， 每个通道代表其对应的一个卷积核与输入图像卷积后的结果

• 因此输出图像的通道数=所用卷积核的个数

补零 padding

如果不补零，两个问题：

• 随着卷积层数增多，得到的特征图尺寸会越来越小【补零可以使卷积后的特征图和输入图像的尺寸保持一致】
• 位于图像边缘的点相对位于图像较中心的点来说被计算的次数少【比如角落的点可能只被卷积核覆盖过一次，而位于中心的点则会被多次覆盖】

两种补零方式：

• valid: 不补零

• same: 补零一定尺寸使得输出的特征图尺寸和补零前的输入图像一致。假设卷积核移动步长为1，则n + 2p - f + 1 = n，n是原图尺寸，p是补零尺寸，f是卷积核尺寸

  filter size	padding
  3 * 3	1
  5 * 5	2
  7 * 7	3

参数计算

image size of output from layer l-1 = \(n_H^{l-1} * n_W^{l-1} * n_C^{l-1}\)

filter size of layer l = $ f^{l} $

padding: valid, so \(p = 0\)

stride of layer l =\(s^{l}\)

number of filters at layer l = \(n_f^l\)

\(n_H^{l} = \frac{n_H^{l-1} +0 -f^l}{s^l}+1\), $ n_W^l $ also can be computed using the same formula

\(n_C^{l} = n_f^l\) 即该层输出的特征图通道个数与该层使用的卷积核个数一致

池化层 Pooling layer

池化是用于压缩特征图中包含的空间信息，与卷积的过程类似，同样需要定义一个窗口，逐步移动该窗口使其扫描整个图像；与卷积不同的是，池化一般不会补零。池化的目的是压缩信息，而卷积的目的是提取特征。

池化层的超参数：

• f ( filter尺寸 )
• s ( stride移动步长 )
• 池化层的超参数并不是通过网络的学习得出，而是直接指定。(因为梯度传播并不会影响这些超参数)

假设输入图像是 h * w * c，根据池化层filter的尺寸(长和宽)还有移动的步长，得到输出的图像 h' * w' * c

池化层输出尺寸h' w'的计算和卷积层的公式一样

【注意】通道数不发生变化，池化层是对每一个特征图分别做pooling，并不会像卷积层那样把每个通道的结果相加！

*【注意】 pooling选择的stride 一般保证不会出现overlap，而不同于一般的卷积层 经常出现overlap *

池化层的类型：

• 最大池化Max pooling：每个窗口操作后的结果是当前区域内的像素最大值。

• 同样也可以定义：平均池化，或是最小池化

  

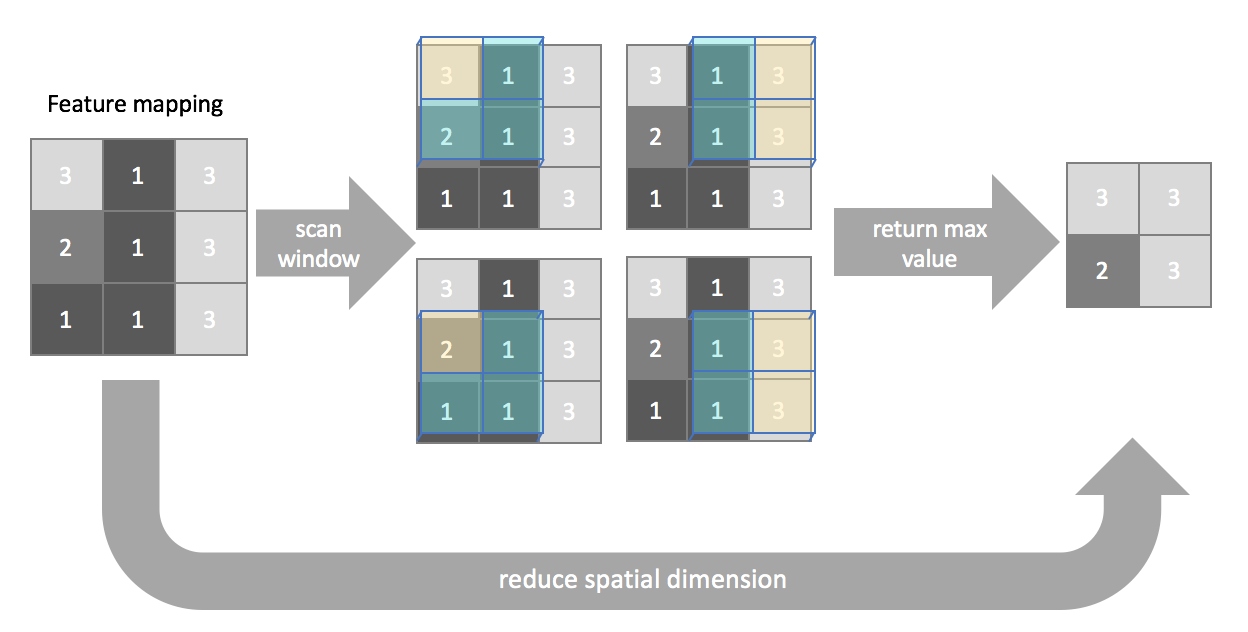
• 全局池化Global pooling：比较极端的情况，窗口的尺寸和图像的尺寸一致，池化之后，每个尺寸为n * n的图像被压缩为一个1 * 1的单一的值。这适用于那些输入图像的尺寸各不相同的CNN，因为它能够将任意的w * h *c 的图像压缩成 1 * 1 * c 的特征图。【只要给出的池化窗口尺寸和输入图像的尺寸一致即可】

全连接层 Fully connected layer FC层

经典的CNN结构 = 卷积层+池化层+全连接层，全连接层一般放在网络结构中的靠后部分

全连接层给CNN带来局限

CNN的局限之一是只能输入固定尺寸的图像到网络，如果尺寸不一致需要进行裁剪或缩放等预处理：

• 在全连接层需要将二维图像拉成一维向量，假设输入全连接层的特征图尺寸是 r * w , 全连接层的神经元是 k 个, 则全连接层的权重个数是 r * w * k。

• 如果训练网络时一直用的输入图像尺寸是 n * m 使得输入全连接层的特征图是 r * w，而在测试阶段(test or predict phase)时输入网络的图像不是 n * m，则会导致输入全连接层的特征图尺寸与 r * w 不一致，即与全连接层的参数（权重）个数不一致！

VGGNet通过将全连接层等价转换成卷积层来改进这一问题 [这样的网络是Fully Convolutional Network (FCN)]

• 转换成卷积层还有一个好处是：参数变少，原本含有FC层的网络，观察每一层的参数个数，发现大多数参数是集中在FC层，而卷积层的参数相对较少（因为卷积操作是权值共享），因此将FC层转换成卷积层可减少参数个数，从而提高训练速度等等。

CNN的一些性质

不变性 invariant

CNN具有平移不变形，一定程度的旋转不变形和缩放不变形，但是剧烈地旋转和缩放则难以识别

平移不变性　translation invariant

因为卷积核是平滑滤波，即如果输入图像的特征移动，输出的特征图也随着移动，但不会影响识别：

• 如果用于训练网络的人脸图像中，人脸都出现在图像的左上角，而在测试网络时输入的人脸图像中，人脸出现在右下角，并不会影响识别结果

旋转不变性 和 缩放（尺度）不变性

由于最大池化层的存在，尽管发生细微的旋转或缩放，可能在感受野区域内的最大值仍没有变化，因此使用最大池化层仍能取到恰当的最大值

• The pooling regimes make convolution process invariant to translation, rotation and shifting. Most widely used one is max-pooling. You take the highest activation to propagate at the interest region so called receptive field. Even a images are relatively a little shifted, since we are looking for highest activation, we are able to capture commonalities between images.

反向传播梯度消失

https://zhuanlan.zhihu.com/p/33006526

梯度反向传播，基于梯度下降策略，以目标的负梯度方向调整参数， \(w^{t+1}=w^{t}+\Delta w\)

求梯度用链式法则，记 \(f_i=f(w_i*f_{i-1}),\) 则 $ \Delta w_2=\frac{\partial Loss}{\partial f_4}\frac{\partial f_4}{\partial f_3}\frac{\partial f_3}{\partial f_2}\frac{\partial f_2}{\partial w_2}$

Loss是最后一层的输出，f4是输入；f4是倒数第二层的输出，f3是输入…… 可见中间的部分就是在每一层对激活函数求导，如果求导结果大于1，随着层数增多，梯度会越来越大，产生梯度爆炸；如果求导结果小于1，梯度更新信息将会以指数形式衰减，发生梯度消失

因此，不同的层 学习的速度（参数更新的速度）差异很大，靠近输出的层学习情况很好，靠近输入的层学习的很慢，（靠近输出的层更新梯度不需要对太多层链式求偏导），甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。。

激活函数使用sigmoid或tanh，导数都是小于1的，很容易发生梯度消失。。

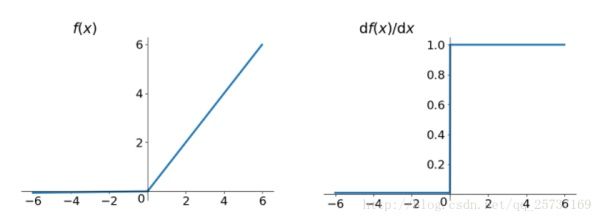
可以改用ReLU, Leak ReLU, eLU等激活函数：

• ReLU 及其导数，可以看到在大于0的部分其导数是恒等于1的

常规框架

CNN，包含一些卷积层，某些阶段还有降采样(pooling or stride convolutions)

• 卷积层用于产生特征图，其用不同的方式解释输入图像
• 池化层压缩空间维度，减少在之后的层里待提取特征的参数数量
• 一般的结构可以表示成: [(CONV-RELU) * N-POOL?] * M-(FC-RELU) * K , SOFTMAX
  对图像分类问题，我们最后会将原始的输入压缩成 a deep stack of(一堆?) 1 * 1的特征图，然后将这些结果喂到几个全连接层来计算 p(class|image) 的概率 (似然)。

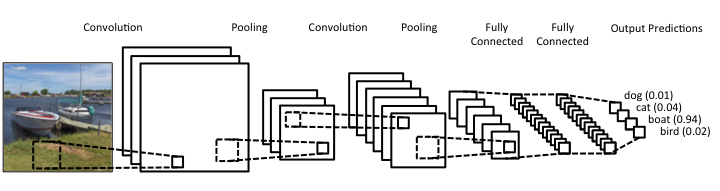
1. CNN的OVERVIEW，通用框架

   https://www.jeremyjordan.me/convnet-architectures/

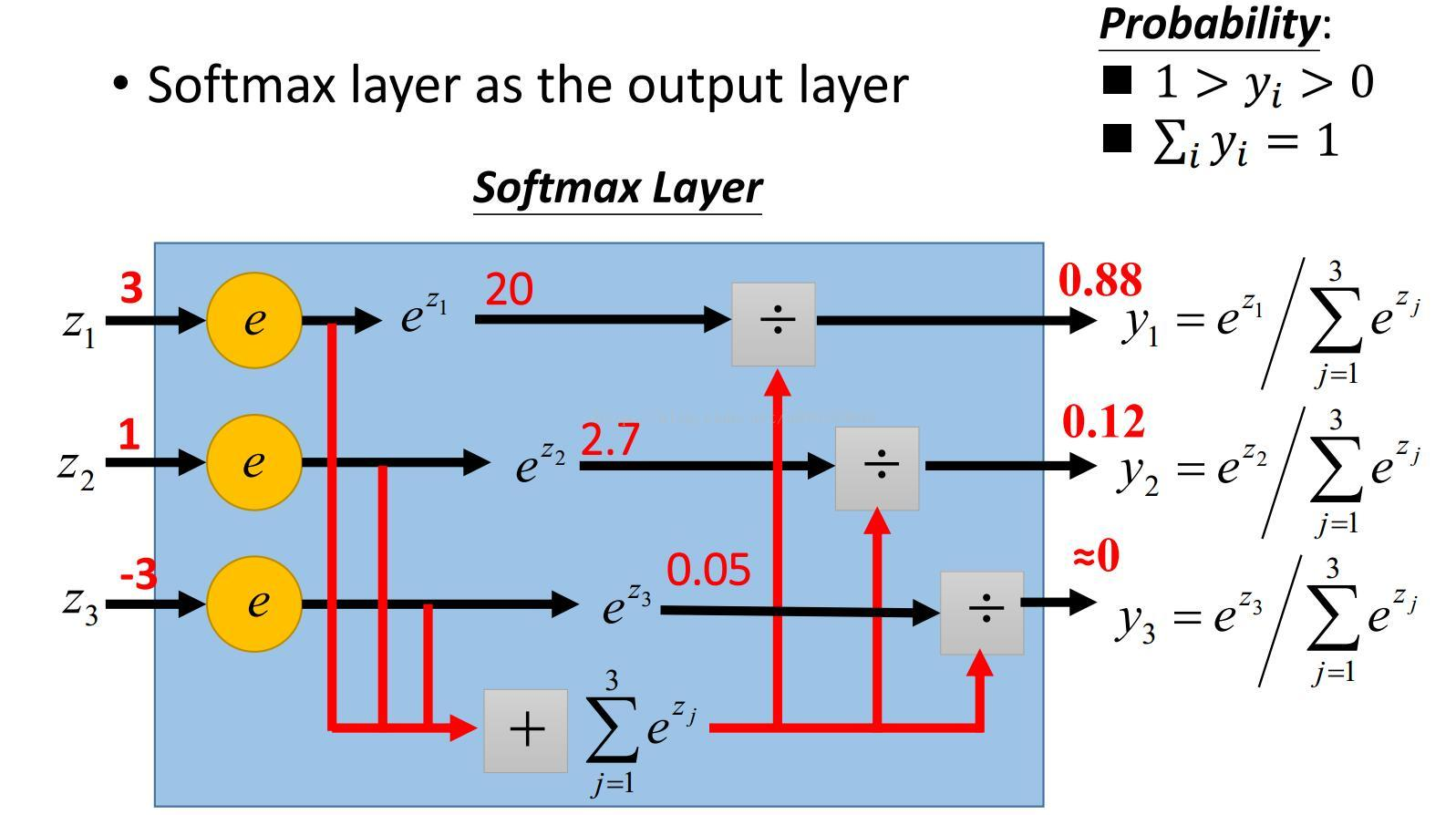
   ReLU 是激活函数的一种。softmax用在最后作归一化。

2. ReLU 激活函数，\(f(x) = max(0,x)\)，即神经元的输入为x，通过激活函数后神经元的输出为f(x)

3. softmax，将多个神经元的输出映射到(0,1)区间 ， \(S_i =\frac{e^i}{\sum_je^j}\)

   

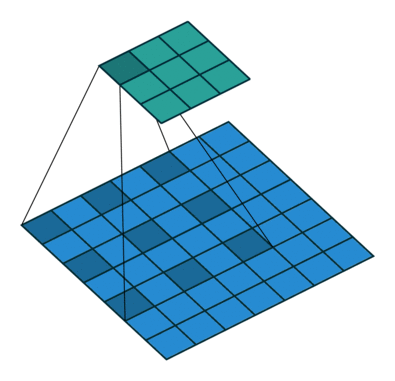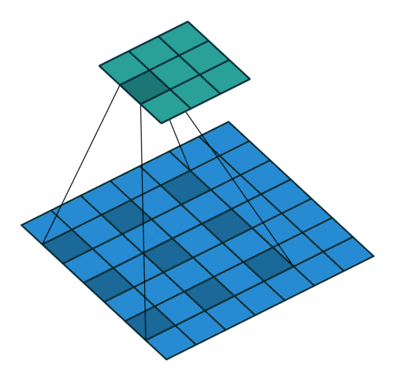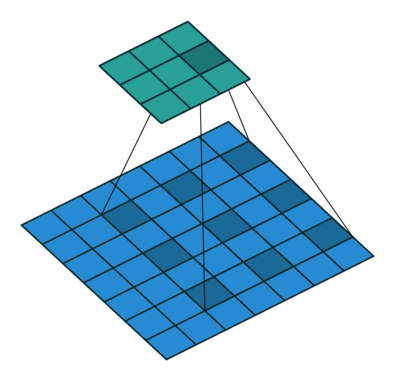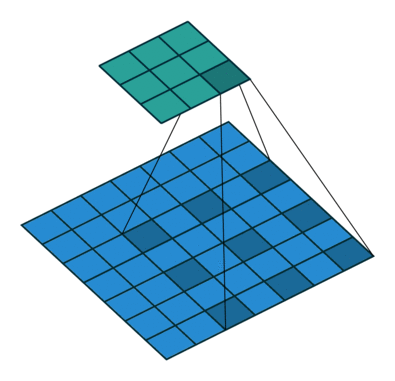
trick

#空洞卷积 dialted convolution

https://www.zhihu.com/question/54149221

工作原理： 卷积核有间隔。即在标准的convolutional map里注入空洞，以此来增加感受野。

下图中的图一是标准卷积，图二是空洞卷积

空洞卷积多了一个超参数称为dilation-rate，指的是kernel的间隔数量，标准的卷积dilation rate是1

图一

图二

#随机丢弃 dropout

https://blog.csdn.net/stdcoutzyx/article/details/49022443

在训练时，按照一定概率将一些网络节点暂时丢弃(失活)。对于随机梯度下降来说，由于是随机丢弃，因此每个mini-batch都在训练不同的网络。

作用：有利于改善CNN中费时、过拟合的缺点

#批正则化 Batch Normalization

https://blog.csdn.net/fate_fjh/article/details/53375881

#迁移学习 transfer learning

使用他人训练好的网络，可以作为自己网络的pre-trained model 即用别人训练好的参数来初始化自己的网络 而不是直接随机初始化参数

进一步的，可以只训练softmax层 以及 最后几层，而前面的层就直接使用别人训练好的网络，这样可以节省训练时间，而且在自己的数据集不够充分的情况下，使用他人在大数据集上训练好的网络而不是自己从零开始训练整个网络，有更好的精度。

#数据增强 data augmentation

【下面说的是对图片，在computer vision领域】

common augmentation method

• 镜像操作mirroring、随机裁剪random cropping、旋转rotation

color shifting

• 对色彩值做一些扰动 (motivation 室外和室内不同光照条件下会对图片颜色产生影响，引入颜色干扰或色彩变化 可以使算法在应对图像色彩变化时健壮性更好)

同样的，数据增强也包含有一些超参数，来代表需要添加什么程度的扰动

同样的，这些超参数最好可以通过先去参考他人的例子，来作为一个好的起步

tips for doing well on benchmarks/winning competitions

• ensembing 训练多个网络，然后将多个网络的结果求平均作为最终结果
• multi-crop at test time 在测试阶段对输入图像进行5次crop (中间+四角) 再分别输入到网络中 对结果求平均 上面两种都算是模型集成 model ensemble
• 以上方法会耗费较多计算资源，不推荐用于产品化的系统

参考资料：

https://www.jeremyjordan.me/convolutional-neural-networks/

https://www.cnblogs.com/SnakeHunt2012/archive/2013/02/18/2916232.html 一个他人的笔记

Stanford cs231n 课程