[六]基础数据类型之浮点数简介

Java中,基本数据float 和double的包装类Float和Double都是浮点类型

所以对于浮点数在计算机中的表示方法需要有一个基本了解,否则很难了解清楚Float和Double的实现原理

本文对计算机中的浮点数表示IEEE754标准,进行了简单介绍

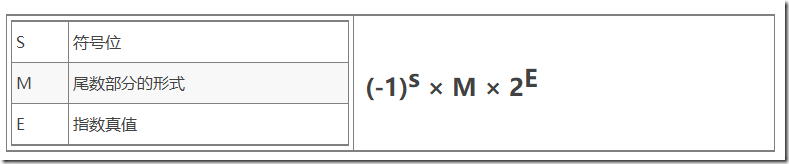
浮点数的表示

IEEE754 标准

  

 

 

因为指数有正有负，指数位中我们就要拿出第一位来指示符号,但是处理起来会不方便

所以给指数的真值 加上 指数偏移值 ，就能保证结果总是一个非负数  

标准规定

指数偏移值为  2(e−1) -1  e为指数的位数

单精度  指数偏移值为127     对于双精度  指数偏移值为1023  

指数无符号数表示的范围

单精度8位   0~255

双精度11位 0~2047

指数真值也就是实际的值

单精度 -127 ~ 128

双精度 -1022 ~ 1023

不过头尾 被保留, 会另做他用 ,下面会继续说明
所以实际的值要去掉头尾,也就是

单精度 -126 ~ 127

双精度 -1022 ~ 1023

规范化形式

综上,一个实数在计算机中表示形式为:

sign  s          符号位
exponent     指数部分
fraction        尾数部分

按照我们上面讲的,指数真值也就是实际的值

单精度 -127 ~ 128

双精度 -1022 ~ 1023

也就是不包括头尾, 也就是指数部分不包括 指数全是0 (0) 或者全是1(255)的情况 

这就是规范化形式,对于规范化形式,表示的数值如下

 

S = 符号位

M=1.f

E=指数值-指数偏移值

表示的数值为:

这是浮点数的规范化表示形式
S表示符号位
尾数部分前隐含一个小数点,小数点前隐含一个1
指数的真值E 也就是 指数部分表示的无符号数减掉指数偏移值

取值范围

单精度

单精度指数的范围(指数 - 指数偏移值之后的值 )  为:
-126 ~ 127

正数最大值
指数为正数的最大值 127
尾数 也为最大值 全部都是1  也就是23个1
(-1)0  × 1.11111...(23个1)  × 2127 
也就是
(2−2−23)×2127

 

1.11111...(23个1)  = 20 +2-1 +2-2 + ....2-23

 

 

公比 q= 1/2    a1 = 20

代入公式 

正数最小值

指数为负数的最小值 -126

尾数 也为最小值, 全部都是0  也就是23个0

1.0  ×  2-126

 

双精度

双精度指数的范围(指数 - 指数偏移值之后的值 )  为:

-1022 ~ 1023

正数最大值

指数为正数的最大值 1023

尾数 也为最大值 全部都是1  也就是52个1

(-1)0  * 1.11111...(52个1)  * 21023 

也就是

(2−2−52)×21023   (还是等比数列求和)

正数最小值

指数为负数的最小值 -1022

尾数 也为最小值, 全部都是0  也就是52个0

1.0 × 2-1022  

非标准化形式

试想,对于单精度 1.001×2−125  和1.01×2−125, 它们的差值是0.001×2−125=1.0×2−128

两个数值之间的差小于能够表示的最小值

也就意味着两个不相等的数进行减法运算,将会瞬间下溢, 得到的结果将会是0

其实这就是精度不够的问题

所以又规定了非标准化形式

那么怎么区分什么时候是标准什么时候是非标准呢? 就是使用保留的指数的取值范围 

对于指数部分,如果所有的比特位全都是0 ,那么这就是一个非标准化形式

在非标准化情况下,尾数部分之前有隐含的小数点, 但是小数点之前,隐含的不在是1 而是0 

对于指数的真值,不再是指数部分表示的无符号数减掉指数偏移量

一旦指数部分为0  (也就是所有的比特位都是0),这就是一个标记符号了,不再有指数大小的含义

这种情况下 

指数的真值为  1 - 指数偏移量

单精度为 1-127= -126

双精度为 1-1023 = -1022

单精度  (−1)s ×  (0.f)  ×  2-126  
双精度  (−1)s ×  (0.f)  ×  2-1022

 

取值范围

很显然,对于非标准化形式来说,指数的真值变成了固定值

想要获得正数的最小值,只需要最后一位为1 其他所有的尾数部分全都是0即可

单精度	0.0000...1(23位,最后一位为1)  ×  2-126   =  2-23 ×  2-126  =  2-149
双精度	0.0000...1(52位,最后一位为1)  ×  2-1022 = 2-52 ×   2-1022 = 2-1074

 

特殊值

指数部分表示的无符号数,头尾被保留,用于表示一些特别的含义

对于标准化形式,指数部分 既不是全0  也不是全1

非标准化情况下,指数部分为全0

当指数部分中所有bit的值全是1，f中所有bit的值全是0，表示无穷大

根据符号位来区分正无穷和负无穷

当指数部分中所有bit的值全是1，f中所有bit的值不全是0  表示NaN(Not a Number)

如果 指数 是0 并且 小数部分 是0, 这个数是0 根据符号位区分+0  和  -0