递归

一、递归算法核心

1）何为递归

递归简单来说就是在运行过程中不断调用自己，直到碰到终止条件，返回结果的过程。

递归可以看作两个过程，分别是递和归：

• 递就是原问题把要计算的结果传给子问题；
• 归则是子问题求出结果后，把结果层层返回原问题的过程。

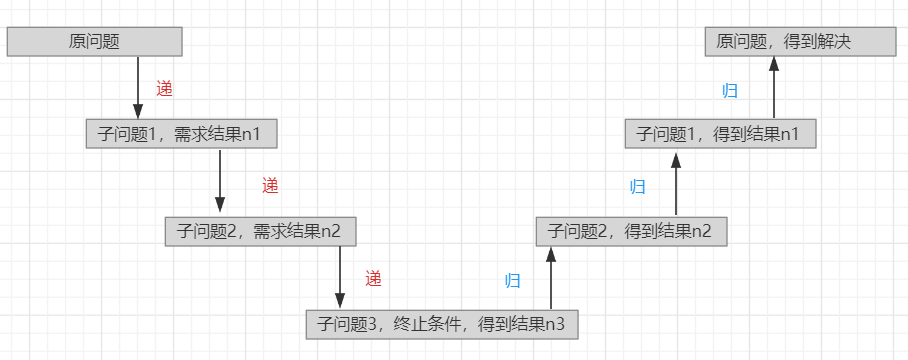
2）递归适用场景

适用递归的问题必须满足三点：

1. 原问题可以拆分为若干个子问题
2. 子问题与原问题除数据规模不同，求解思路完全相同
3. 存在递归终止条件

满足以上条件的问题适用递归算法求解。

递归求解的关键就是：当不满足终止条件时如何缩小函数值使其进入下一层循环，即找到将原问题层层拆分的方法。

3）简单示例

斐波那契数列：有一个数列：1、1、2、3、5、8、13、21、34…，求该数列的第 n 项的值是多少。

通过观察发现斐波那契数列的规律是：从第三个数开始，第n个数是第n-1和第n-2个数之和。

这显然满足递归求解的三个前置条件：

1. 求第n个数，可以拆分为求第n-1个数和第n-2个数
2. 第n-1个数又是第n-2个数和第n-3个数之和，和原问题求解思路完全相同
3. 终止条件是n-1或者n-2，即等于1

上面观察发现的规律即是原问题层层拆分的方法！

代码：

public static int Fibonacci(int num){
     if (num==1||num==2){ //终止条件
           return 1;
     }
     return Fibonacci(num-1)+Fibonacci(num-2); //递归进入下一循环
}

---

二、递归进阶

有些问题的规律并不能直接观察得出，需要一定的分析才能发现，以经典的汉诺塔问题为例：

柱子A上有n个按大小顺序放置的圆片，要全部移动到另一根柱子C上，每次只能移动一个，可以借助柱子B，且小的不能在大的下面。求最少的移动次数。

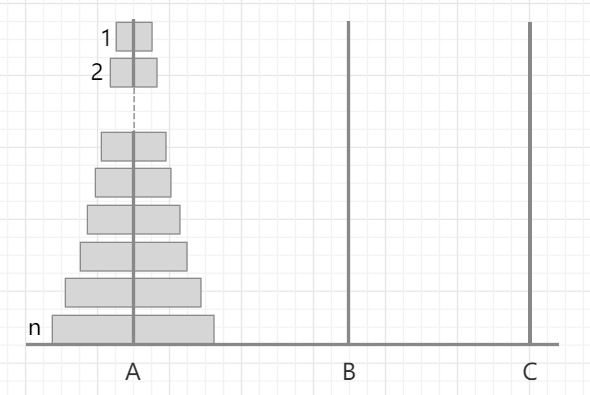
通过数学归纳法发现其规律：

• 当n=1时，只需从A->C，移动1次。
• 当n=2时，先让1号从A->B，再让2号从A->C，最后让1号从B->C，移动3次。
• 当n=3时，可以将1、2号看做一个子问题整体，先让1、2号从A->B，再让3号从A->C，最后让1、2号从B->C。由n=2可以得知，移动两片需要3次，而1、2号从A->B，再从B->C共进行了两次，所以共有6次，再加上3号A->C的过程，要移动7次。
• 同理，当n=4时，可以将1、2、3看做一个子问题整体，共要移动2×7（n=3的移动次数）+1=15次。

所以，汉诺塔的数学规律则是：当n=n时，要移动2×(n-1)+1次。

代码：

public static int TowerOfHanoi(int num){
     if (num==1){  //终止条件，只有一块圆盘时，直接A->C
         return 1;
     }
     return TowerOfHanoi(num-1)*2+1;  //否则，进入下一循环
}

总结：递归算法在实际应用中，要有将子问题看做一个整体的思维，在寻找原问题与子问题之间的缩小规律时，暂不必考虑子问题内部拆分；那是下一循环才需要考虑的问题。如此，才能将问题简化，更快地发现缩小问题规模的方法！